文本分类（TFIDF/朴素贝叶斯分类器/TextRNN/TextCNN/TextRCNN/FastText/HAN）

简介

通常，进行文本分类的主要方法有三种：

• 基于规则特征匹配的方法（如根据喜欢，讨厌等特殊词来评判情感，但准确率低，通常作为一种辅助判断的方法）
• 基于传统机器学习的方法（特征工程 + 分类算法）
• 给予深度学习的方法（词向量 + 神经网络）

自BERT提出以来，各大NLP比赛基本上已经被BERT霸榜了，但笔者认为掌握经典的文本分类模型原理还是十分有必要的。这一节，将对一些经典模型进行介绍，并在我的github中给出部分模型的实现。

TFIDF

TF-IDF（term frequency–inverse document frequency）是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。TF意思是词频(Term Frequency)，IDF意思是逆文本频率指数(Inverse Document Frequency)。

TFIDF的主要思想是：如果某个词或短语在一篇文章中出现的频率TF高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。其统计公式如下：

\(tfidf_{i, j} = tf_{i, j} \times idf_{i, j}\)

其中，tf表示词频(Term Frequency)，即词条在文档i中出现的频率；idf为逆向文件频率(Inverse Document Frequency)，表示某个关键词在整个语料所有文章中出现的次数的倒数（该指标用于降低常用词的重要性）。

优点：能过滤掉一些常见的却无关紧要的词语，同时保留影响整个文本的重要词语。

缺点：不能有效反应特征词的分布情况，也没有体现词语的位置信息（通常文章首尾句词的重要性较高）。

朴素贝叶斯分类器

朴素贝叶斯分类器是文本分类常用的机器学习方法。贝叶斯分类器的核心思想就是贝叶斯决策论：贝叶斯决策论考虑如何基于某个先验分布下，使得平均风险最小的决策。该理论具有两个最两个关键的部分：先验分布和平均风险

贝叶斯公式

文本分类问题最简单的方法，就是通过对文本所包含的字词特征来对文本进行归类。假设类别为\(Y\)，文本特征集合为\(X\)，用概率统计的方法来表示，则我们需要求得条件概率\(P(Y|X)\)。如果我们将贝叶斯决策论的思想应用到该问题中，即我们熟知的贝叶斯公式：

\(P(Y|X) = \frac{P(Y)P(X|Y)}{P(X)}\)

其中，\(P(Y|X)\)为后验概率；\(P(X)\)和\(P(Y)\)为先验概率。

我们可以将贝叶斯公式的右端拆成\(P(Y)\)与\(\frac{P(X|Y)}{P(X)}\)乘积的形式，则我们可以将其理解为在X的条件下Y发生的概率，等于Y发生的概率乘以一个修正因子，若修正因子大于1，表明X条件的发生使得Y发生的概率变大了，修正因子小于1，则表明X条件使得Y发生个概率降低了。由于概率因子中，\(P(X)\)是一个确定值(可以通过统计得到)，我们只需要确定条件概率\(P(X|Y)\)，即可确定给定文本特征的情况下该条件概率分布，从而进行文本分类。

贝叶斯决策论的理解

假设我们的文本由N种可能的类别标记，即\(Y={c_1, c_2, ..., c_N}\)，则我们可以由后验概率\(P(c_i|x)\)得到将样本\(x\)分类为\(c_i\)的条件风险(或称期望损失)：

\(R(c_i|x)=\sum_{j=1}^{N}\lambda_{ij}P(c_j|x)\)

其中，\(\lambda_{ij}\)表示将\(c_i\)标记为\(c_j\)产生的损失
如果我们想要得到最优的分类，就需要使得每次标记的条件风险最小化，即最优条件风险：

\(h^*(x)=argmin_{c \in Y}R(c|x)\)

这就是贝叶斯判定准则，如果我们想使得分类错误率(1-正确分类率)最小，则只需令条件风险为：

\(R(c|x)=1 - P(c|x)\)

则最优条件风险简化为

\(h^*(x)=argmin_{c \in Y}R(c|x)=argmax_{c \in Y}P(c|x)\)

我们将贝叶斯公式带入其中，可得

\(h^*(x)=argmax_{c \in Y}P(c|x)=argmax_{c \in Y}\frac{P(c)P(x|c)}{P(x)}=argmax_{c \in Y}P(c)P(x|c)\)

综合以上讨论，当前求最小化分类错误率的问题转化成了最大化后验概率\(P(x|c)\)的问题。

极大似然估计

我们已经假设输入文本特征满足某种条件概率分布，接下来的关键是由观测到的文本特征对该条件概率分布进行参数估计，即极大似然估计。

极大似然估计源自于频率学派，他们认为参数虽然未知，但却是客观存在的规定值，因此，可以通过优化似然函数等准则确定参数数值。

假设\(D_c\)表示训练集中c类标签的样本集合，假设这些样本是独立同分布的。求解极大似然估计主要由如下几个步骤：

• 由训练集的特征集合以及事先假设的概率分布函数，写出似然函数

\(P(D_c|\theta)=\prod_{x \in D_c}P(x|\theta)\)

• 由于很多小概率的乘积会导致浮点数下溢出，我们对其求对数，将原来的乘积运算变为求和运算

\(L(\theta)=logP(D_c|\theta)=\sum_{x \in D_c}logP(x|\theta)\)

• 当\(L(\hat \theta)\)取得极大值时，\(\theta\)的极大似然估计为\(\hat \theta\)，即

\(\hat \theta = argmax_{\theta}L(\theta)\)

朴素贝叶斯分类器

从上一节可知，我们可以用极大似然的方法来估计我们需要的概率分布参数，接下来的关键就是我们如何从训练样本中准确估计出条件概率P(x|c)。我们知道文本之间的相互关系是十分复杂的，但为了简化模型复杂度从而更简单的估计出条件概率，朴素贝叶斯分类器做了“属性条件独立性假设”：对已知类别，假设所有属性相互独立，即假设每个属性独立的对分类结果发生影响，即

\(P(x|c)=\prod_{i=1}^{d}P(x_i|c)\)

有了条件概率的简化条件之后，我们很容易将贝叶斯准则改写为

\(h^*(x)=argmax_{c \in Y}P(c|x)=argmax_{c \in Y}P(c)\prod_{i=1}^{d}P(x_i|c)\)

上式即朴素贝叶斯的表达式。

接下来，我们从训练集中统计得到似然估计，令\(D_c\)表示训练集D中第c类样本组成的集合，先验概率\(P(c)\)的似然估计为:

\(P(c)=\frac{|D_c|}{|D|}\)

对于条件概率\(P(x|c)\)，通常，我们假设该条件概率满足某种概率分布，在sklearn中有三种假设的分布：GuassianNB、MultinomialNB和BernoulliNB(分别假设为高斯分布、多项分布和伯努利分布，文本分类通常使用多项式分布)，假设满足多项式分布，则条件概率为如下形式：

\(P(X=x_{jl}|Y=c_k) = \frac{x_{jl}+\lambda}{m_k+n\lambda}\)

其中，\(m_k\)是训练集中输出为第k类的样本个数，\(\lambda\)取1时即拉普拉斯平滑，目的是防止0概率估计的出现，而影响后验概率的计算结果。

总的来说，朴素贝叶斯分类的推导主要基于贝叶斯公式，决策方式为在“属性条件独立性假设”条件下的贝叶斯决策论，参数估计的方法为极大似然估计。

TextRNN

之前介绍过词向量以及三大特征提取器，这里就不再赘述了，深度学习模型无非就是用特征抽取器拼接起来的不同结构的神经网络模型，所以接下来的几个部分基本是对模型结构的简介。
首先我们来看看用经典的LSTM/GRU实现文本分类模型的基本结构：

由上图可知，TextRNN仅仅是将Word Embedding输入到双向LSTM中，然后对最后一位的输出输入到全连接层中，在对其进行softmax分类即可。

TextCNN

对于TextCNN在上一篇文章中简单的提到过，这里再做一些简单的补充，其模型结构如下图所示：

上图很直观的展现了，与图像中的二维卷积不同，TextCNN中采用的是一维卷积，每个卷积核的大小为\(h \times k\)(h为卷积核的窗口大小，k为词向量的维度)，文中采用了多种不同尺寸的卷积核，用以提取不同文本长度的特征(上图种可以看见，卷积核有h=2, 3, 4三种)

然后，作者对于卷积核的输出进行MaxPooling，目的是提取最重要的特征。将所有卷积核的输出通过MaxPooling之后拼接形成一个新向量，再将该向量输出到全连接层分类器(Dropout + Linear + Softmax)实现文本分类。

TextRCNN

这篇论文中描述稍微复杂了点，实际模型非常简单，该模型结构如下图所示：

该模型的主要思想如下：

• 首先获得词向量表示\(e(w_i)\)
• 其次将词向量通过双向RNN(实践中可以是LSTM或GRU)得到\(c_l(w_i)\)和\(c_r(w_i)\)
• 将\(c_l(w_i)\), \(e(w_i)\)以及\(c_r(w_i)\)拼接得到新的向量，将其输入到全连接网络对其进行整合，激活函数为tanh
• 再将全连接网络的输出进行MaxPooling
• 最后将其输入一个全连接分类器中实现分类

原文链接

FastText

FastText是Facebook于2016年发布的文本分类模型，其主要思想基于word2vec中的skip-gram模型（关于skip-gram模型参考我之前词向量的博客，这里也就不再赘述），在训练文本分类模型的同时，也将训练出字符级n-gram词向量。

通常认为，形态类似的单词具有相似的语义特征。而对于Word2Vec模型，其构建的语料库中，把不同的单词直接映射到独立的id信息，这样，使得不同单词之间的形态学信息完全丢失了，如英文中的“nation”和“national”，中文中的“上海市政府”和“上海市”。如果能够学习到形态学变换到单词特征的规则，我们可以利用这个规则来得到许多训练集中不可见的单词表示。

为了解决这个问题，FastText用字符级别的n-gram来表示一个单词或句子，如

中华人民共和国
bigram：中华 华人 人民 民共 共和 和国
trigram：中华人 华人民 人民共 民共和 共和国

得到了词的n-gram表征之后，我们可以用n-gram子词（subword）的词向量叠加来表示整个词语，词典则是所有词子词的并集。

其主要模型结构如下图所示，最后也采用了层次softmax的提速手段：

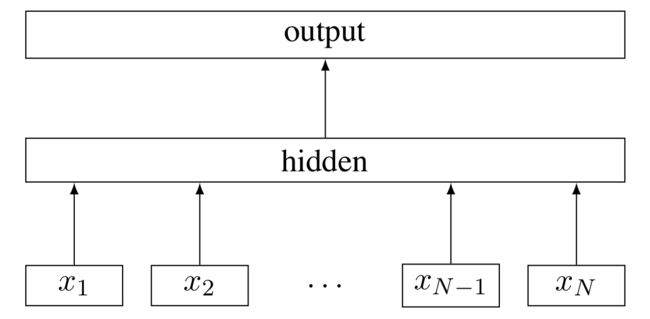
对比skip-gram模型，可以FastText的词典规模会更大，模型参数会更多。但每一个词的词向量都是子词向量的和，使得一些生僻词或未出现的单词能够从形态相近的单词中得到较好的词向量表示，从而在一定程度上能够解决OOV问题

原文链接

HAN

HAN的全称为Hierarchical Attention Network(分级注意网络)，从字面意思就可以理解其是一个分层架构模型。该模型主要用于文档分类(长文本分类)，其主要结构如下所示：

HAN主要由两个层次的模型架构：词级别和句级别，每个层次的模型都包括一个编码器和注意力模型两个部分，整个模型的细节如下：

• 如上图所示，假设我们的文档中有\(L\)个句子，对于第二个句子，单词长度为\(T\)
• 首先将单词输入Embedding层获取词向量
• 将获取的词向量输入词编码器，即一个双向GRU，将两个方向的GRU输出拼接在一起得到词级别的隐向量\(h\)
• 将词级别的隐向量通过一个单层感知机(MLP，实际上就是全连接神经网络，激活函数选用tanh)，输出的结果可以看作是更高层次的隐向量表示：
  \(u_{it}=tanh(W_wu_{it}+b_w)\)
• 随机初始化一个上下文向量\(u_w\)(随着训练不断优化)，将该上下文向量\(u_w\)与高层次的隐向量表示\(u_{it}\)输入softmax，得到每个词与上下文向量的相似度表示：
  \(\alpha_{it}=\frac{exp(u_{it}^Tu_w)}{\sum_texp(u_{it}^Tu_w)}\)
• 将上述相似度作为权重，对\(h_{it}\)加权求和得到句子级别的向量表示：
  \(s_i=\sum_t\alpha_{it}h_{it}\)
• 对于句子级别的向量，我们用相类似的方法，将其通过编码层，注意力层，最后将文档中所有句子的隐向量表示加权求和，得到整个文档的文档向量\(v\)，将该向量通过一个全连接分类器进行分类。

其实HAN中使用到的的Attention就是最常用的 Soft-Attention ，整个模型的结构就相当于TextRNN + Soft-Attention的叠加。，分别用来处理词级别和句子级别，对于短文本分类，我们只需借鉴词级别的模型即可。

原文链接

Highway Networks

门限神经网络(Gated Networks)，在之前一篇文章中也提到过，主要是利用\(sigmoid\)函数“门限”的性质，来实现对信息流的自动控制的一种方法，Highway Networks就是一种典型的门限网络结构，这里也简单的介绍一下。

根据原文的定义，假设原来网络的输出为：
\[y = H(x, W_H)\]

其中\(H(·)\)表示非线性变换(可以设置为激活函数为relu的全连接层)。定义\(T(x, W_T) = sigmoid(W_T^Tx + b_T)\)文章的做法就是将其改进为：
\[y = H(x, W_H) \cdot T(x, W_T) + x \cdot (1-T(x, W_T))\]

则对于输出y，有：
\[y = \begin{cases} x, & if\ T(x, W_T) = 0 \\ H(x, W_H), & if \ T(x, W_T) = 1 \end{cases}\]

原文链接

https://blog.csdn.net/zhangph1229/article/details/52106301
https://www.kesci.com/home/project/5be7e948954d6e0010632ef2
https://zhuanlan.zhihu.com/p/32091937
https://zhuanlan.zhihu.com/p/64603089
https://zhuanlan.zhihu.com/p/24780258
https://zhuanlan.zhihu.com/p/32965521
https://zhuanlan.zhihu.com/p/63111928
https://zhuanlan.zhihu.com/p/53342715
https://zhuanlan.zhihu.com/p/44776747