一、数据结构绪论
- 逻辑结构与物理结构
- 逻辑结构:集合、线性(一对一)、树(一对多)、图(多对多)
- 物理结构:顺序存储结构、链式储存结构
- 抽象数据类型 (Abstract Data Type,ADT):是指一个数学模型及定义在该模型上的一组操作
标准格式
ADT 抽象数据类型名
Date 数据元素之间的逻辑定义
Operation
操作1
初始条件
操作结果描述
操作2
......
操作3
......
endADT
二、算法
- 算法特性:输入输出、确定性、又穷性、可行性
- 算法要求:正确性、健壮性、可读性、时间效率高和存储量低
- 算法时间复杂度
- 推导大O阶方法
1.用常数1取代运行时间中所有加法常数
2.在修改后的运行函数中,只保留最高位
3.如果最高阶项存在且不是1,则去除与这个项相乘的常数
得到的结果是大O阶
- 推导大O阶方法
三、线性表
- 定义:零个或多个数据元素的有限序列
- 抽象数据结构
ADT 线性表
Data :
线性表的数据对象集合为{a1,a2,......,an},每个元素的类型均为DataType。其中,除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
Operation:
InitList(&l)
操作结果:构造一个空的线性表L
DestroyList(&l)
初始条件:线性表已存在
操作结果:销毁线性表L
ClearList(&l)
初始条件:线性表已存在
操作结果:置线性表L为空表
ListEmpty(L)
初始条件:线性表已存在
操作结果:若线性表L为空表,则返回TRUE,否则返回FALSE
ListLenght(L)
初始条件:线性表已存在
操作结果:返回线性表L数据元素个数
GetElem(L,i,&e)
初始条件:线性表已存在(1≤i≤ListLenght(L))
操作结果:用e返回线性表L中第i个数据元素的值
locatElem(L,e,comare())
初始条件:线性表已存在,comare()是数据元素判定函数
操作结果:返回线性表L中第1个与e满足关系comare()的数据元素的位序
PriorElem(L,cur_e,&pre_e)
初始条件:线性表已存在
操作结果:若cur_e是线性表L的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败,pre_e无定义
NextElem(L,cur_e,&)
初始条件:线性表已存在
操作结果:若cur_e是线性表L的数据元素,且不是第最后一个,则用next_e返回它的后继,否则操作失败,next_e无定义
ListInsert(&L,i,e)
初始条件:线性表已存在(1≤i≤ListLenght(L)+1)
操作结果:在线性表L中第i个数据元素之前插入新元素e,L长度加1
ListDelete(&L,i,&e)
初始条件:线性表已存在(1≤i≤ListLenght(L))
操作结果:删除线性表L中第i个数据元素,用e返回其值,L长度减1
ListTraverse(L,visit())
初始条件:线性表已存在
操作结果:依次对线性表L的每个数据元素调用visit()函数,一旦visit()失败,则操作失败}ADT List
- 顺序储存结构代码
#define MAXSIZE 20
typedef int ElemType;
typedef struct{
ElemType data[MAXSIZE];
int length;
}SqList;
单链表、静态链表、循环链表、双向链表
- 单链表
- 单链表储存结构代码
typedef struct node{
ElemType data;
struct Node *next;
} Node;
typedef struct Node *LinkList;
- 静态链表(早期没有指针,用数组代替指针)
- 静态链表的储存结构代码
#define MAXSIZE 1000
typedef struct{
Elemtype data;
int cur;/游标/
}Component,StaticLinkList[MAXSIZE];
 静态链表
静态链表
头指针存放备用链表(后面空闲空间)第一个节点下标
数组最后一个元素的cur用来存放头结点(第一个插入元素的下标)
循环链表
将单链表中的终端结点的指针端由空指针改为指向头结点,链表就形成了一个环-
双向链表
- 双向链表的储存结构代码
typedef Struct DulNode{
ElemType data;
struct DuLNode *prior;
struct DuLNode next;
}DulNode,DuLinkList;
- 双向链表的储存结构代码
四、栈与队列
栈
- 栈的定义:限定仅在表尾进行插入和删除操作的线性表
- 栈的抽象数据类型
ADT 栈(stack)
Data :
同线性表
Operation:
InitStack(*S)
初始化操作,建立一个空栈*S
DestroyStack(*S)
若栈存在,则销毁它
ClearStack(*S)
将栈清空
StackEmpty(*S)
若栈为空,则返回true,反之返回false
GetTop(S,*e)
若栈存在且非空,用e返回栈顶元素
Push(*S,e)
若栈存在,插入新元素e到栈S中并成为栈顶元素
Pop(S,e)
删除栈S中栈顶元素,并用e返回其值
StackLengh(S)
返回栈S的元素个数
endADT
- 栈的顺序存储结构
typedef int SElemType;
typedef struct{
SElemtype data[MAXSIZE];
int top;
}SqStack; - 两栈共享空间
typedef struct{
SElemType data[MAXSIZE];
int top1;
int top2;
}sqDoubleStack;
判断是否满栈
top1+1==top2
-
栈的链式存储结构
typedef struct StackNode{
SElemType data;
struct StackNode next;
}StackNode,LinkStackPtr;typedef struct LinkStack{ LinkStack top; int count; }LinkStack; 栈的应用:
四则运算表达式求值:后缀表示法(逆波兰表示法)。
队列
- 队列的定义:只允许在一端进行插入操作,而在另一端进行删除操作的线性表
- 队列的抽象数据类型
ADT 队列(Queue)
Data :
同线性表
Operation:
InitQueue(*Q)
初始化操作,建立一个空队列*Q
DestroyQueue(*Q)
若队列存在,则销毁它
ClearQueue(*S)
将队列清空
QueueEmpty(*Q)
若队列为空,则返回true,反之返回false
GetHead(Q,*e)
若队列存在且非空,用e返回队头元素
EnQueue(*Q,e)
若队列Q存在,插入新元素e到队列Q中并成为队尾元素
DeQueue(Q,e)
删除队列Q中队头元素,并用e返回其值
QueueLengh(Q)
返回队列Q的元素个数
endADT
- 循环队列
- 定义:队列头尾相接
- 循环队列顺序存储结构
typedef int QElemType;
typedef struct{
QElemType data[MAXSIZE];
int front;
int rear;
}SqQueue;
队列满的条件是
######(rear+1)%QueueSize == front
- 队列的链式储存结构
typedef int QElemType;
typedef struct QNode{
QElemType data;
struct QNde next;
}QNode,QueuePtr;
typedef struct{
QueuePtr font,rear;
}LinkQueue;
五、串
- 串的定义:串是由零个或多个字符组成的有限序列,又名叫字符串
- 串的抽象数据结构
ADT 串(string)
Data
串中元素仅由一个字符组成,相邻元素具有前驱和后继关系
Operation
StrAssign( &T, chars )
初始条件:chars是字符串常量。
操作结果:生成一个其值等于chars的串T。
StrCopy( &T, S )
初始条件:串S存在。
操作结果:由串S复制得串T。
StrEmpty( S )
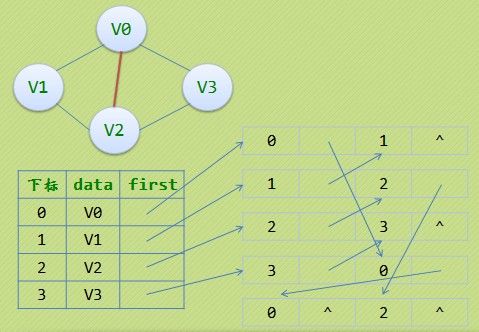
初始条件:串S存在。 初始条件:串S存在。 初始条件:串S存在。 初始条件:串S1和S2存在。 初始条件:串S存在,1≤pos≤StrLength(S)且0≤len≤StrLength(S)-pos+1 初始条件:串S和T存在,T是非空串,1≤pos≤StrLength(S)。 初始条件:串S,T和V存在,T是非空串。 初始条件:串S存在,1≤pos≤StrLength(S)-len+1。 初始条件:串S存在。 树的定义 树是n个结点的有限集。n=0时称为空树。在任何一棵非空树: 结点的度:结点拥有的子树数,度为零的称为叶节点(终端结点) 树的度是节点的度的最大值 结点的层次从根开始定义,根为第一层,树中结点的最大层次称为树的深度(高度) 树的抽象数据类型 ADT 树(tree) 双亲表示法 孩子表示法 线性表储存结点元素,孩子链表的孩子结点 child是数据域,储存某结点在表头数组中的下标。next是指针域,用来存储指向某结点的下一个孩子的指针 孩子兄弟表示法 二叉树 定义 存储结构 遍历二叉树 根左右 线索二叉树 因为此时p结点的后继还没有访问到,因此只能对它的前驱界限pre的右指针rchild做判断,if(!pre->rchild)表示如果为空,则p就是pre的后继,于是pre->rchild=p,并且设置pre->RTag=Thread,完成后继结点的线索化 ADT 图(Graph) 与上一章的孩子表示法思路相同 ![边集数组]XO.png](http://upload-images.jianshu.io/upload_images/1318539-703d9b755b44bc94.png?imageMogr2/auto-orient/strip%7CimageView2/2/w/1240) 【data、firstin、firstout】【tailvex、headvex、headlink、taillink】 容易求得顶点的出度和入度 邻接多重表
操作结果:若S为空串,则返回TRUE,否则返回FALSE。 StrCompare( S, T )
初始条件:串S和T存在。
操作结果:若S>T,则返回值>0;若S=T,则返回值=0;若SStrLength( S )
操作结果:返回S的元素个数,称为串的长度。ClearString( &S )
操作结果:将S清为空串。Concat( &T, S1, S2 )
操作结果:用T返回由S1和S2联接而成的新串。SubString( &Sub, S, pos, len )
操作结果:用Sub返回串S的第pos个字符起长度为len的子串。Index( S, T, pos )
操作结果:若主串S中存在和串T值相同的子串,则返回它在主串S中第pos个字符之后第一次出现的位置;否则函数值为0。Replace( &S, T, V )
操作结果:用V替换主串S中出现的所有与T相等的不重叠的子串。 ######StrInsert( &S, pos, T )
初始条件:串S和T存在,1≤pos≤StrLength(S)+1。
操作结果:在串S的第pos个字符之前插入串T。StrDelete( &S, pos, len )
操作结果:从串S中删除第pos个字符起长度为len的子串。DestroyString( &S )
操作结果:串S被销毁。
}
endADT
一个一个匹配
算法思想:利用已经匹配过的数据,创建一个next数组。避免重复遍历
难点:理解next数组六、树
(1)有且仅有一个特定的称为根的结点
(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集t1、t2、......、tm,其中每一个集合本身又是一棵树,并且称为根的子树
Data
树是由一个根节点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
Operation
endADT
#define MAX_TREE_SIZE 100
typedef int ElemType;
typedef struct PTNode{
TElemType data;
int parent;
}PTNode;
typedef struct
{
PTNode nodes[MAX_TREE_SIZE];
int r,n;/根的位置和结点数/
}PTree;#define MAX_TREE_SIZE 100
typedef int ElemType;
typedef struct CTNode{
int child;
struct CTNode *next;
}*ChildPtr;
typedef struct
{
TElemType data;
ChildPtr firstchild;
}CTBox;
typedef struct
{
CTbox nodes[MAX_TREE_SIZE];
int r,n;
}CTree;
typedef int ElemType;
typedef struct CSNode{
TElemType data;
struct CSNode firstchild,rightsib;
}CSNode,*CSTree;
是n个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个跟结点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
从根节点开始遍历二叉树,遇到没有则置空
typedef struct BiTNode{
TElemType data;
struct BiTNode lchild,rchild;
} BiTNode,*BiTree;
* 中序遍历
>左根右
* 后序遍历
>左右根
typedef enum{Link,Thread} PointerTag;
typedef struct BiThrNode
{
TElemType data;
struct BiThrNode lchild,rchild;
PointerTag LTag;
PointerTag RTag;
} BiThrNode,*BiThrTree;
void InThreading(BiThrTree p)
{
if(p) {
InThreading(p->lchild);//左子树线索化
if(!p->lchild){
p->LTag=Thread;
p->lchild=pre;}//前驱线索
if(!pre->rchild){
pre->RTag=Thread;
pre->rchild=p;}//后续线索
pre=p; //保持pre指向p的前驱
InThreading(p->rchild);//右子树线索化
}
}//InThreading
七、图
Data
顶点的有穷非空集合和边的集合
Operation
endADT
typedef char VertexType;
typedef int EdgeType;
#define MAXVEX 100
#define INFINITY 65355
typedef struct{
VertexType vexs[MAXVEX];/顶点数组/
EdegeType arc[MAXVEX][MAXVEX];
int numVertexes,numEdges;
}MGraph;
typedef char VertexType;
typedef int EdgeType;
typedef struct EdgeNode{
int adjvex; /*邻接点域,存储该顶点的对应下标*/
EdgeType weight;/*存储权值*/
struct EdgeNode *next;
}EdgeNode;
typedef struct VertexNode{
VertexType data;
EdgeNode firstedge;
}VertexNode,AdjList[MAXVEX];
typedef struct{
AdjList adjList;
int numVertexes,numEdges;
}GraphAdjList;
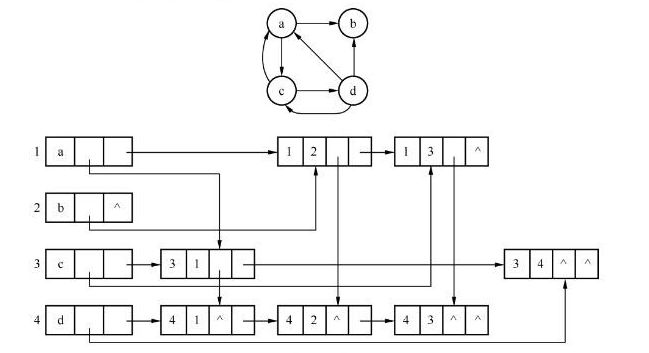
* 边集数组
* 十字链表
从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发,深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到(邻接表)
类似于树的前序遍历(队列)
八、查找
九、排序