深度学习入门笔记(五):神经网络的编程基础
专栏——深度学习入门笔记
声明
1)该文章整理自网上的大牛和机器学习专家无私奉献的资料,具体引用的资料请看参考文献。
2)本文仅供学术交流,非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益,还望海涵,并联系博主删除。
3)博主才疏学浅,文中如有不当之处,请各位指出,共同进步,谢谢。
4)此属于第一版本,若有错误,还需继续修正与增删。还望大家多多指点。大家都共享一点点,一起为祖国科研的推进添砖加瓦。
文章目录
- 专栏——深度学习入门笔记
- 声明
- 深度学习入门笔记(五):神经网络的编程基础
- 1、Jupyter/iPython Notebooks快速入门
- 2、Python 中的广播
- 3、关于numpy向量的说明
- 4、编程框架的选择问题
- 推荐阅读
- 参考文章
深度学习入门笔记(五):神经网络的编程基础
1、Jupyter/iPython Notebooks快速入门
学到现在,你需要知道常用的python的编译器,推荐使用anaconda而不是官方的python,这样的话更容易安装各种第三方库,如何安装可以看一下这个博客——Windows10 下 Anaconda和 PyCharm 的详细的安装教程(图文并茂)。
至于IDE的话,pycharm 适合于大型项目的编写和调试,Jupyter Notebook 适合于学习和数据挖掘探索,这里我们就快速地学习一下 Jupyter Notebook 工具。

这就是 Jupyter Notebook 的界面,让我快速地讲解下它的一些特性。

这里有一些空白区域的代码块,可以编写代码,而较长的灰色区域就是代码块。

比如,编写打印输出著名的程序员入门语句——Hello World 的代码,然后执行这一代码块,最终,它就会输出我们想要的 Hello World。

在运行一个单元格 cell 时,你也可以选择运行其中的一块代码区域。通过点击 Cell 菜单的 Run Cells 执行这部分代码。
在你的计算机上,运行 cell 的键盘快捷方式是 Ctrl + enter。但是也可以使用 shift + enter 来运行 cell,不过这样会默认跳转到下一个代码区域。

当阅读指南时,如果不小心双击了它,点中的区域就会变成 markdown 语言形式。如果不小心使其变成了这样的文本框,只要运行下单元格 cell,就可以回到原来的形式。所以,点击 cell 菜单的 Run Cells 或者使用 Ctrl + enter,就可以使得它变回原样。markdown 格式可以用来写笔记,以免自己忘记了代码中的知识。

这里还有一些其他的小技巧。比如当执行上面所使用的代码时,它实际上会使用一个内核在服务器上运行这段代码。如果你正在运行超负荷的进程,或者电脑运行了很长一段时间,或者在运行中出了错,又或者网络连接失败,这里依然有机会让 Kernel 重新工作。你只要点击 Kernel,选择 Restart,它会重新运行 Kernel 使程序继续工作。
所以,如果只是运行相对较小的工作并且才刚刚启动你的台式电脑或笔记本电脑,这种情况应该是不会发生的。但是,如果你看见错误信息,比如 Kernel 已经中断或者其他信息,你可以试着重启 Kernel,这样就简单地重启程序了。

当使用 Notebook 时会有多个代码区域块。尽管并没有在前面的代码块中添加自己的代码,但还是要确保先执行这块代码。因为在这个例子,它导入了 numpy 包并另命名为 np 等,并声明了一些可能需要的变量。为了能顺利地执行下面的代码,就必须确保先执行上面的代码,即使不要求写其他的代码,这样其他程序就可以默认是在这些库的调用下运行了。

最后就是编译环境的选择,正常情况下 Notebook 的编译环境是默认的,但是你也可以自己新建一个环境,这个具体操作在这个博客中——Windows10 下 Anaconda和 PyCharm 的详细的安装教程(图文并茂),比如我这里新建的环境 Pytorch for Deeplearning,就是专门为 pytorch 的学习而建立的,可以通过 Kernel 下的 Change kernel,选择 Pytorch for Deeplearning,就ok了。

这个就是默认的 kernel。

这个是我自己建的 kernel。
你会发现这种交互式的 shell 命令,在 Notebooks 是非常有用的,能使你快速地实现代码并且查看输出结果,便于学习,同时还可以记录在这个过程中的想法。好好学习它的使用,你会发现更多的惊喜。
2、Python 中的广播

这是一个不同食物(每100g)中不同营养成分的卡路里含量表格,表格为3行4列,列表示不同的食物种类,从左至右依次为苹果(Apples),牛肉(Beef),鸡蛋(Eggs),土豆(Potatoes)。行表示不同的营养成分,从上到下依次为碳水化合物,蛋白质,脂肪。
那么,现在假设我们想要计算不同食物中不同营养成分中的卡路里百分比,应该怎么做?
以计算苹果中的碳水化合物卡路里百分比含量为例,首先计算苹果(Apples)(100g)中三种营养成分卡路里总和 56+1.2+1.8 = 59,然后用 56 / 59 = 94.9% 算出结果。可以明显地看出苹果(Apples)中的卡路里大部分来自于碳水化合物(Carb),而牛肉(Beef)则不同。对于其他食物,计算方法类似。首先,按列求和,计算每种食物中(100g)三种营养成分总和,然后分别用不用营养成分的卡路里数量除以总和,计算百分比。
那么,能否在向量化(深度学习入门笔记(四):向量化)的基础上用代码完成这样的一个计算过程呢?
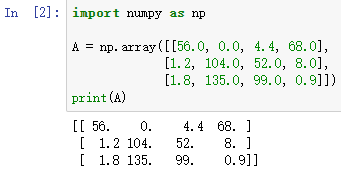
当然是可以的,假设上图的表格是一个4行3列的矩阵 A A A,记为 A 3 × 4 A_{3\times 4} A3×4,接下来使用 Python 的 numpy 库完成这样的计算。使用两行代码就可以完成整个过程,第一行代码对每一列进行求和,第二行代码分别计算每种食物每种营养成分的百分比。
在 jupyter notebook 中输入如下代码,按 Ctrl + Enter 运行,输出如下:
下面再计算每列的和,可以看到输出是每种食物(100g)的卡路里总和。

其中 sum 的参数 axis=0 表示求和运算按列执行,之后会详细解释。
接下来计算百分比,这条指令将 3 × 4 3\times 4 3×4 的矩阵 A A A 除以一个 1 × 4 1 \times 4 1×4 的矩阵,得到了一个 3 × 4 3 \times 4 3×4 的结果矩阵,这个结果矩阵就是要求的百分比含量。
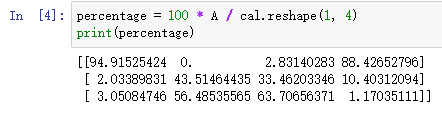
到这里问题就解决了,现在来解释一下 A.sum(axis = 0) 中的参数 axis。axis用来指明将要进行的运算是沿着哪个轴执行,在numpy中,0轴是垂直的,也就是列,而1轴是水平的,也就是行。 而第二个 A / cal.reshape(1, 4) 指令则调用了 numpy 中的广播机制。这里使用 3 × 4 3 \times 4 3×4 的矩阵 A A A 除以 1 × 4 1 \times 4 1×4 的矩阵 c a l cal cal。技术上来讲,其实并不需要再将矩阵 c a l cal cal reshape (重塑)成 1 × 4 1 \times 4 1×4,因为矩阵 c a l cal cal 本身已经是 1 × 4 1 \times 4 1×4 了。但是当我们写代码的过程中出现不确定矩阵维度的时候,通常会对矩阵进行重塑来确保得到想要的列向量或行向量。重塑操作 reshape 是一个常量时间的操作,时间复杂度是 O ( 1 ) O(1) O(1),它的调用代价极低,所以使用是没问题的,也推荐大家使用。
那么一个 3 × 4 3 \times 4 3×4 的矩阵是怎么和 1 × 4 1 \times 4 1×4 的矩阵做除法的呢?来看一些广播的例子:

在 numpy 中,当一个 4 × 1 4 \times 1 4×1 的列向量与一个常数做加法时,实际上会将常数扩展为一个 4 × 1 4 \times 1 4×1 的列向量,然后两者做逐元素加法。结果就是右边的这个向量。这种广播机制对于行向量和列向量均可以使用。
再看下一个例子。

用一个 2 × 3 2 \times 3 2×3 的矩阵和一个 1 × 3 1 \times 3 1×3 的矩阵相加,其泛化形式是 m × n m \times n m×n 的矩阵和 1 × n 1 \times n 1×n 的矩阵相加。在执行加法操作时,其实是将 1 × n 1 \times n 1×n 的矩阵复制成为 m × n m \times n m×n 的矩阵,然后两者做逐元素加法得到结果。针对这个具体例子,相当于在矩阵的第一列全部加100,第二列全部加200,第三列全部加300。这就是在前面例子中计算卡路里百分比的广播机制,只不过那里是除法操作,这里是加法操作(广播机制与执行的运算种类无关)。
下面是最后一个例子。
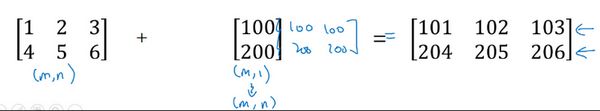
这里相当于是一个 m × n m \times n m×n 的矩阵加上一个 m × 1 m \times 1 m×1 的矩阵。在进行运算时,会先将 m × 1 m \times 1 m×1 矩阵水平复制 n n n 次,变成一个 m × n m \times n m×n 的矩阵,然后再执行逐元素加法。
广播机制的一般原则如下:
- 首先是 numpy 广播机制
这里的广播和播音广播是完全不同的,它的要求是什么呢?什么样的条件下可以使用广播?
要求:如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1,则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。
如何计算后缘维度的轴长度?可以使用代码 A.shape[-1] 即矩阵维度元组中的最后一个位置的值,就是矩阵维度的最后一个维度,比如卡路里计算的例子中,矩阵 A 3 , 4 A_{3,4} A3,4 后缘维度的轴长度是4,而矩阵 c a l 1 , 4 cal_{1,4} cal1,4 的后缘维度也是4,故满足了后缘维度轴长度相符的条件,可以进行广播。广播会在轴长度为1的维度上进行,轴长度为1的维度对应 axis=0,即垂直方向,矩阵 c a l 1 , 4 cal_{1,4} cal1,4 沿 axis=0 (垂直方向)复制成为 c a l T e m p 3 , 4 calTemp_{3,4} calTemp3,4 ,之后两者进行逐元素除法运算。
简单概括总结就是,先变成一样大,再逐元素除法。
矩阵 A m , n A_{m,n} Am,n 和矩阵 B 1 , n B_{1,n} B1,n 进行四则运算,后缘维度轴长度相符,符合条件,可以广播,广播沿着轴长度为1的轴进行,即 B 1 , n B_{1,n} B1,n 广播成为 B m , n ′ {B_{m,n}}' Bm,n′ ,之后做逐元素四则运算。
矩阵 A m , n A_{m,n} Am,n 和矩阵 B m , 1 B_{m,1} Bm,1 进行四则运算,后缘维度轴长度不相符,但其中一方轴长度为1,符合条件,可以广播,广播沿着轴长度为1的轴进行,即 B m , 1 B_{m,1} Bm,1 广播成为 B m , n ′ {B_{m,n}}' Bm,n′ ,之后做逐元素四则运算。
矩阵 A m , 1 A_{m,1} Am,1 和常数 R R R 进行四则运算,后缘维度轴长度不相符,但其中一方轴长度为1,符合条件,可以广播,广播沿着缺失维度的轴进行,缺失维度就是 axis=0,轴长度为1的轴是 axis=1,即 R R R 广播成为 B m , 1 ′ {B_{m,1}}' Bm,1′ ,之后做逐元素四则运算。
3、关于numpy向量的说明
Python 的特性允许你使用 广播(broadcasting) 功能,这是 Python 的 numpy 程序语言库中最灵活的地方,但这是程序语言的优点,也是缺点。
- 优点的原因,在于它们创造出语言的表达性,Python 语言巨大的灵活性使得你仅仅通过一行代码就能做很多事情。
- 缺点的原因,由于广播巨大的灵活性,有时候对于广播的特点以及广播的工作原理这些细节不熟悉的话,可能会产生很细微或者看起来很奇怪的 bug。
为了演示 Python-numpy 的一个容易被忽略的效果,特别是怎样在 Python-numpy 中构造向量,来做一个快速示范。
首先设置 a = n p . r a n d o m . r a n d n ( 5 ) a=np.random.randn(5) a=np.random.randn(5),这样会生成存储在数组 a a a 中的5个高斯随机数变量;然后输出 a a a,从屏幕上可以得知,此时 a a a 的 shape(形状) 是一个 ( 5 , ) (5, ) (5,) 的结构同样地, a . T a.T a.T 的 shape 也是这样的。这在 Python 中被称作 一个一维数组。它既不是一个行向量也不是一个列向量,这也导致它有一些不是很直观的效果。
比如 a a a 和 a a a 的转置阵最终结果看起来一样,shape 也是一样的。但是输出 a a a 和 a a a 的转置阵的内积,你可能会想, a a a 乘以 a a a 的转置,返回的可能会是一个矩阵。但如果这样做,你只会得到一个数。

所以在编写神经网络时,不要使用 shape 为 (5,)、(n,) 或者其他一维数组的数据结构。相反,设置 a a a 为 ( 5 , 1 ) (5,1) (5,1),这样就是一个5行1列的向量。在先前的操作里 a a a 和 a a a 的转置看起来一样,而现在这样的 a a a 变成一个新的 a a a 的转置,并且它是一个行向量。当输出 a a a 的转置时有两对方括号,而之前只有一对方括号,所以这就是 1行5列的矩阵和一维数组的差别。
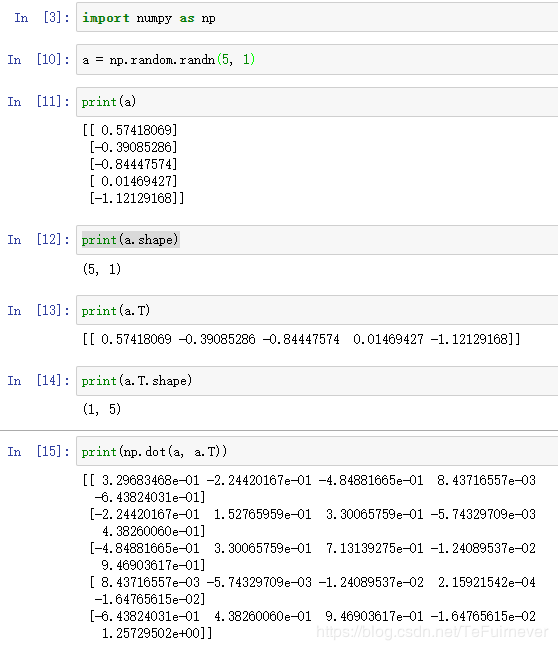
如果这次再输出 a a a 和 a a a 的转置的乘积,会返回一个向量的外积,也就是一个矩阵。这就符合我们的预期了,也就是在可控范围内了,因为你知道自己的代码输出是什么了。
除了,输入确定维度的矩阵或向量之外,还有一件事,就是如果你不能完全确定一个向量的维度,建议你扔一个 断言语句(assertion statement) 进去。这样,就可以确保在这种情况下是否是一个 ( 5 , 1 ) (5,1) (5,1) 向量了,或者说是一个列向量。
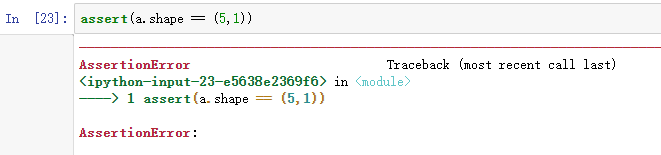
如果不对的话,就会报一个叫做 AssertionError 的错误!!!
4、编程框架的选择问题
这个我在 大话卷积神经网络CNN(干货满满) 中讲过,目前主流的是 Google的TensorFlow、Facebook的pytorch 还有 百度的paddlepaddle,如果是研究的话,我建议使用TensorFlow,因为它更好理解一下基础原理,而不是单纯的调包侠。大话卷积神经网络CNN(干货满满) 博客中也写了相关的资源推荐,这里就不详细说了。
推荐阅读
- 深度学习入门笔记(一):深度学习引言
- 深度学习入门笔记(二):神经网络基础
- 深度学习入门笔记(三):求导和计算图
- 深度学习入门笔记(四):向量化
- 深度学习入门笔记(五):神经网络的编程基础
- 深度学习入门笔记(六):浅层神经网络
- 深度学习入门笔记(七):深层神经网络
- 深度学习入门笔记(八):深层网络的原理
- 深度学习入门笔记(九):深度学习数据处理
- 深度学习入门笔记(十):正则化
- 深度学习入门笔记(十一):深度学习数据读取
- 深度学习入门笔记(十二):权重初始化
参考文章
- 吴恩达——《神经网络和深度学习》视频课程