读书笔记之《高等数学》---第一章 函数与极限

第一节 映射与函数

映射
映射：两个非空集合X、Y，如果存在法则f使得X中的每个元素x在Y中都有唯一一个确定的元素y，则称法则f是从X到Y的映射
像：y称为x的像
原像：x称为y的原像
定义域：X集合称为定义域
值域：Y集合称为值域

构成一个映射必须具备的三个要素：定义域、值域、法则f
满射：Y中的任意一个元素y都是X中的某个元素的像
单射：对于X中任意两个元素x1不等于x2，则有f(x1)不等于f(x2)
一一映射：既是单射也是满射
逆映射：首先映射f必须是单映射，y=f(x)必定存在x=g(y)，法则g是法则f的逆映射
复合映射：多个映射复合，例如y=f(g(x))，g(x)的值域必须包含于f(x)的定义域

函数
函数：设数集D包含与R，则称映射f：D->R是定义在D上的函数，记为y=f(x)，x是自变量，y是因变量，D是定义域，y的取值范围是值域
函数可分为连续函数与分段函数
函数的几种特性：

1. 函数的有界性：在定义域D中如果任意x都使得f(x)<=K,则函数有上界，K是函数的一个上界，如果任意x使得f(x) <= N，则函数有下届，N是函数的一个下届
2. 函数的单调性：在定义域的一个区间中，单调递增或单调递减
3. 函数的奇偶性：f(-x) = f(x)为偶函数，f(-x) = -f(x) 为奇函数
4. 函数的周期性：在函数定义域D中，如果存在 l 使得 f(x+l) = f(x) 则函数是周期函数，l是函数f(x)的周期
   反函数：D->f(D)是单射，则存在逆映射f^-1：f(D) -> D,则称该逆映射是f的反函数
   复合函数：多个函数复合例如y=f[g(x)]

函数运算：

1. 和差：（f±g)(x) = f(x)±g(x)
2. 积：(f * g)(x) = f(x) * g(x)
3. 商：(f/g)(x) = f(x) / g(x)\

初等函数：

第二节 数列的极限

数列的定义：按照某一个法则，对于每一个n包含与N+，对应着一个确定的实数xn,这些实数按照下标从小到大排列构成一个序列
数列中的每一个元素叫做数列的项，第n项叫做数列的一般项
定义： 设{xn}为一个数列，如果存在常数a，对于任意给定的ε（不论它多么小），总存在正整数N，是得当n>N时，不等式 |xn-a| < ε成立，则称常数a时数列{xn}的极限，或该数列收敛于a。
该定义的目的是判断一个数列是极限是否是a
主要应用：我们根据上面的定义，任意给定一个数ε（这个数是个变量，代表无穷小），然后根据定义求出N（如果存在的话），使得当n>N时上面的不等式 |xn-a| < ε成立，我们的主要目标是求得这个N，

收敛数列的性质：
定理1（极限的唯一性）：如果数列{xn}收敛，那么它的极限唯一
定理2（收敛数列的有界性）：如果数列{xn}收敛，那么这个数列一定有界
定理3（收敛数列的保号性）：如果数列收敛于a，且a>0(或a<0)，那么存在正整数N，当n>N时，都有xn>0（或xn<0）
定理4（收敛数列与其子数列间的关系）：如果数列{xn}收敛于a，那么它的任一子数列也收敛，且极限也是a。

第三节 函数的极限
在自变量的某一变化过程中，如果对应的函数值无限接近于某个确定的数，这个确定的数称为这一变化过程中函数的极限
主要有两种情形：

1. 自变量x任意地接近于有限值x0或者说趋于有限值x0（记做x–>x0）时对应的函数值f(x)的变化情形
2. 自变量x的绝对值|x|无限增大时即趋于无穷时（记做x–>∞），对应的函数值f(x)的变化情形

x趋于x0时的定义
定义1：设函数f(x)在点x0的某一去心邻域内有定义。如果存在常数A，对于任意给定的正数ε（不论它多么小），总存在正数δ，使得当x满足不等式0<|x-x0|<δ时，对应的函数值f(x)都满足不等式 |f(x) - A| < ε，那么常数A就叫做函数f(x)当x–>x0时的极限。
从x0左边趋于极限称为左极限
从x0右边趋于极限称为右极限

x趋于无穷时的定义
定义2：设函数f(x)当|x|大于某一个正数时有定义。如果存在常数A，对于任意给定的正数ε（不论它多么小），总存在正数X，使得当x满足不等式x>|x|时，对应的函数值f(x)都满足不等式 |f(x) - A| < ε 那么常数A就叫做函数f(x)当x–>∞时的极限。

函数极限的性质：
定理1（函数极限的唯一性）:如果函数极限存在，那么这个极限唯一
定理2（函数极限的局部有界性）：如果f(x)的极限是A，那么存在常数M>0和δ>0，使得点0< |x-x0| < δ,有| f(x) | ≤ M 。
定理3（函数极限的局部保号性）：如果f(x)的极限为A，且A>0（或A < 0），那么存在常数δ > 0，使得点0< |x-x0| < δ, 有f(x) > 0（或f(x) < 0）。
定理3演变定理 ： 如果f(x)的极限为A，A不等于0，那么就存在着x0的某一去心领域Uº(x0)，当x∈Uº(x0)时，就有 |f(x)| > |A|/2。
推论： 如果x0的某一去心领域内f(x) ≥0（或f(x) ≤0），而且f(x)的极限为A，那么A ≥0（或A≤0）
定理4（函数极限与数列极限的关系）：如果f(x)的极限存在，{Xn}，时函数f(x)的定义域内任一收敛于x0的数列，且满足：xn ≠ x0（n ∈ N﹢）,那些相应的函数值数列{ f(xn) }必收敛，且f(xn)，n–>∞ 的极限等于f(x) x–>x0

第四节 无穷小于无穷大
定义1：如果函数f(x)当 x–>x0（或x->∞）时的极限为零，那么称函数f(x)为当 x–>x0（或x->∞）时的无穷小
定理1： 自变量的同一变化过程x–>x0（或x->∞）中，函数f(x)具有极限A的充分必要条件是f(x) = A + α，其中α是无穷小。
该定理可以用于穷函数的极限，当函数f(x) 的分解成一个函数g(x)加常数C，这是g(x)的极限也就是f(x) 的极限

定义2：设函数f(x) 在x0的某一去心领域内有定义（或|x| 大于某一个正数时有定义）。如果对于任意给定的正数M（不论它多大）。总存在正数δ（或正数X），只要x满足不等书0 < |x - x0| < δ（或|x| > X），对应的函数值f(x) 总满足不等式 | f(x) | > M，那么就称 f(x)时当x–>x0（或x–>∞）时的无穷大。
定理2：在自变量同一变化过程中，如果f(x)为无穷大，那么1/f(x)为无穷小；反之，如果f(x)为无穷小，且f(x) ≠ 0 ，那么1/f(x)为无穷大。

第五节 极限运算法则
定理1：两个无穷小的和时无穷小
定理2：有界函数与无穷小的乘积是无穷小
推论1：常数与无穷小的乘积是无穷小
推论2：有限个无穷小的乘积是无穷小
定理3：如果limf(x)=A，limg(x)=B，那么：
lim[f(x) ± g(x)] = limf(x) ± limg(x) = A ± B。
lim[f(x) * g(x)] = limf(x) * limg(x) = A * B。
如果有B ≠ 0 ，则 lim[f(x) / g(x)] = limf(x) / limg(x) = A / B。
推论1：如果 limf(x)存在，而c为常数，那么lim[ cf(x) ] = c limf(x)。
推论2：如果 limf(x)存在，而n是正整数，那么lim[ f(x) ] ⁿ = [ limf(x) ]ⁿ 。
定理4：设有数列{ xn }和{ yn }，如果limxn = A, limyn = B,n–>∞。那么
lim (xn + yn) = A ± B。
lim (xn * yn) = A * B。
当yn ≠ 0（n=1,2,…）且B ≠ 0时，lim xn/yn = A / B 。
定理5：如果 γ(x) ≥ ψ(x) ，而lim γ(x) = A，lim ψ(x) = B，那么A≥B。
定理6（复合函数的极限运算法则）：设函数y = f [ g(x) ] 时由函数 u = g(x) 与函数 y = f(u) 复合而成。 f [ g(x) ] 在点x0的某个去心领域内有定义，若lim g(x) = u0 （x --> x0），lim f(u) = A（u --> u0），且存在δ > 0，当x ∈ U°(x0 , δ0)时，有g(x) ≠ u0,则，
lim f [ g(x) ] = lim f(u) = A 。

第六节 极限存在的准则 两个重要极限
两个重要的极限：

准则1：如果数列{ xn }，{ yn }，及{ zn }满足下列条件：

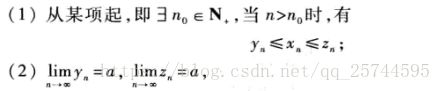
那么数列{ xn }的极限存在，且lim xn = a （n --> ∞）。
夹逼定理：

准则2: 单调有界数列必有极限
准则2推论：设函数f(x) 在点x0的某个左领域内单调有界，则f(x) 在x0 的左极限 f(x0﹣)必定存在
柯西极限存在准则：数列{ xn }收敛的充分必要条件是，对于任意给定的正数ε，存在正数N，使得当m >N , n >N时，有 |xn - xm | < ε。

第七节 无穷小的比较
以下的α及β都是在同一个自变量的 变化过程中的无穷小。

定理1：α与β是等价无穷小的充分必要条件为β = α + o(α);

定理2：

第八节 函数的连续性与间断性
定义： 设函数 y = f(x)在x0的某一领域内有定义，如果

那么就称函数y = f(x) 在点x0连续
定义变式：设函数 y = f(x)在x0的某一领域内有定义，如果lim f(x) = f(x0) ,（x --> x0），那么就称函数f(x)在点x0连续
函数间断点：

1. 当x --> x0时函数趋于无穷，则x0为函数的无穷间断点
2. 当x --> x0时函数在正负之间变动无限多次，则x0为函数的振荡间断点
3. 当x --> x0时函数，当x = x0时，给定函数称为连续时，不是振荡间断点时，为可去间断点
   
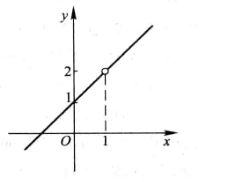
   4.跳跃间断点，如下图：
   

第九节 连续函数的运算与初等函数的连续性
定理1：设函数f(x) 与g(x)在点x0连续，则他们的和（差）f±g、积f * g 及商 f / g都在x0连续。






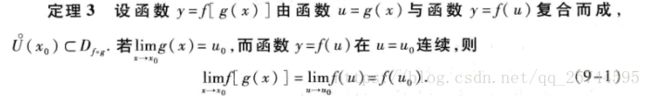
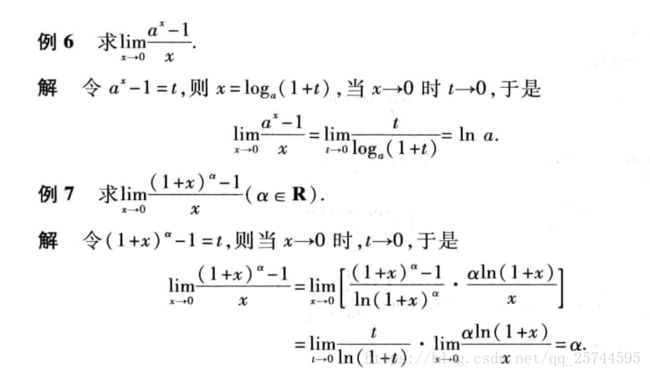
初等函数在它们的定义域内都是连续的。

第十节 闭区间上连续函数的性质
定理1（有界性与最大值最小值定理）：在闭区间上连续的函数在该区间上有界且一定能取得它的最大值和最小值。
定理2（零点定理）：设函数f(x)在闭区间[a , b]上连续，且f(a) 与 f(b) 异号，则在开区间（a ，b）内至少有一点ξ，使得 f(ξ） = 0。
定理3（介值定理）：设函数f(x)在闭区间[ a，b] 上连续，且在这个区间的端点取不同的函数值 f(a) = A ，f(b) = B。则对应A与B之间的任意一个数C，在开区间（a，b）内至少有一点ξ，使得 f(ξ） = C。
推论：在闭区间[ a，b] 上连续的函数f(x)的值域为闭区间[ m, M]，其中m与M依次为f(x) 在[ a，b] 上的最大值与最小值。

一致连续性定义：设函数f(x)在区间I上有定义，如果对于任意给定的正数ε，总存在正数δ，使得对于区间I上的任意的两点x1、x2，当| x1 - x2 | < δ时有| f(x1) - f(x2) | < ε，那么称函数f(x) 在区间I上一直连续。

定理4（一致连续性定理）：如果函数f(x)在闭区间[ a，b] 上连续，那么它在该区间上一致连续。