深度学习神经网络从欠拟合到拟合的调整方法及示例代码
深度学习神经网络从欠拟合到拟合的调整方法及示例代码
1. 深度神经网络结构调整说明
当深度神经网络可以对少量样本进行很好的拟合,而对较多的样本无法很好拟合的时候,很可能是深度网络的层数不够深,即深度网络的特征无法很好地表征所有样本的特征。此时,可以通过加深网络的层次来使得深度网络对较多的样本进行拟合。
另外,深度网络对于分类样本的拟合能力强于对于连续值样本的拟合能力。即同样的深度网络如果能拟合10组分类的样本,可能只能拟合3组连续值的样本。分类样本采用softmaxwithloss作为损失函数,连续值样本采用欧式距离损失函数。以下例子已连续值样本作为拟合的方式。
2. 少样本合适拟合的示例代码
本例包含四组样本,深度网络较好地拟合。网络参数为:
netsize=[inputsize,5,6,8,7,5,4];
(1) Main_function
clear all
clc
close all
TrainData =[1 2 3 4 5 6 7 8 9 10
1 9 17 25 33 41 49 57 65 73];
batchsize=4;
TrainData=TrainData(:,1:batchsize);
TrainLabel=[1 0.3 0.8 0.2;
1.8 0.8 1.2 1.1];
classnum=2;%输出端数目
%获取数据的维度
inputsize=size(TrainData ,1);
%获取数据的数量
datanum=size(TrainData ,2);
% 用一个向量来定义网络的深度,以及每层神经元数目。
netsize=[inputsize,5,6,8,7,5,4];
% netsize=[inputsize,5,6,8,9,9,8,7,5,4];
%网络最后一层神经元数数目,再考虑一个偏置。
lastsize=netsize(end)+1;
%初始化网络参数,以结构体的形式保存。
stack = initializeNet(netsize);
% 在训练时,往往需要将参数转成一列向量,提供给损失函数。
% stack ->stackTheta,netconfig保存一些结构参数。
[stackTheta, netconfig] =stack2params(stack);
% 指定固定的最后一层的初始化的值;
rand('state',2)
lastTheta = 0.0005 * randn(lastsize *classnum, 1);
%最终网络需要的参数
Theta=[ lastTheta ; stackTheta ];
%lastTheta表示深度网络最后一层的权值
% the following part is for the traingepoch.
% batchsize=5;
%%每次训练的小批量样本数
batchnum=floor(size(TrainData,2)/batchsize);
DataNum=size(TrainData,2);
alpha=1e-2;
%这是学习率,一般随着网络的悬念都需要不断的减小
lambda = 1e-4; % Weight decay parameter
for epoch=1:16000
v_epoch=epoch
if epoch>=16000
alpha=1e-3;
end
idx=randperm(DataNum);
for t=1:batchnum
subdata=TrainData(:,idx((t-1)*batchsize+1:(t)*batchsize));
sublabel=TrainLabel(:,idx((t-1)*batchsize+1:(t)*batchsize));
[cost(epoch),grad]=ReLUDNNCost(Theta,classnum,lastsize,netconfig,lambda,subdata,sublabel);
Theta=Theta-alpha*grad;
end
end
plot(log(cost))
(2) drelu
function dre= drelu(x)
dre=zeros(size(x));
dre(x>0)=1;
dre(x==0)=0.5; %这句可以不要
end
(3) relu
function re = relu(x)
re = max(x,0)-1;
end
(4) params2stack
function stack = params2stack(params, netconfig)
depth =numel(netconfig.layersizes);
stack = cell(depth,1);
prevLayerSize =netconfig.inputsize; %the size of the previous layer
curPos = double(1); % mark current position in parametervector
for d = 1:depth
% Create layer d
stack{d} = struct;
% Extract weights
wlen =double(netconfig.layersizes{d} * prevLayerSize);
stack{d}.w =reshape(params(curPos:curPos+wlen-1), netconfig.layersizes{d}, prevLayerSize);
curPos = curPos+wlen;
% Extract bias
blen =double(netconfig.layersizes{d});
stack{d}.b =reshape(params(curPos:curPos+blen-1), netconfig.layersizes{d}, 1);
curPos = curPos+blen;
% Set previous layer size
prevLayerSize =netconfig.layersizes{d};
end
end
(5) ReLUDNNCost
function [cost,grad] =ReLUDNNCost(theta,numClasses,lasthiddenSize, netconfig,lambda,trainData,trainLabels)
%参数获取的一些操作
lastTheta =reshape(theta(1:lasthiddenSize*numClasses), numClasses, lasthiddenSize);
%从theta向量中抽取网络权值参数并转化
stack =params2stack(theta(lasthiddenSize*numClasses+1:end), netconfig);
stackgrad = cell(size(stack));
%这里保存在应用BP算法求梯度时需要的数据
PARA=cell(numel(stack),1);
%传进来的样本数
datanum=size(trainData,2);
%开始前馈,网络虽然多层,但只是重复而已
data=trainData;
for d = 1:numel(stack)
PARA{d}.a=data;
z2=(stack{d}.w*data)+stack{d}.b*ones(1,datanum);
%ReLU函数
a2=relu(z2);
data=a2;
%ReLU函数的导函数
PARA{d}.daz=drelu(z2);
end
a2=[a2;ones(1,datanum)];
%开始求解损失
groundTruth=trainLabels;
v_groundTruth=groundTruth
M = lastTheta*a2;
v_M=M
% 损失函数,
cost=sum(sum((groundTruth-M).^2))./datanum;
%最后一层神经元的目标函数对lastTheta 的导数,
lastThetaGrad =-1/datanum*((groundTruth-M)*a2')+lambda*lastTheta;
% 输出层误差传导至倒数第二层神经元的值
predelta=-lastTheta'*(groundTruth-M);
predelta=predelta(1:end-1,:);
for d = numel(stack):-1:1
delta=predelta.*PARA{d}.daz;
stackgrad{d}.w=delta*PARA{d}.a'/datanum;%.*PARA{d}.idx
stackgrad{d}.b=sum(delta,2)/datanum;
predelta=stack{d}.w'*delta;
end
grad = [lastThetaGrad(:) ;stack2params(stackgrad)];
end
(6) stack2params
function [params, netconfig] = stack2params(stack)
params = [];
for d = 1:numel(stack)
params = [params ; stack{d}.w(:) ;
stack{d}.b(:) ];
end
if nargout > 1
if numel(stack) == 0
netconfig.inputsize = 0;
netconfig.layersizes = {};
else
netconfig.inputsize = size(stack{1}.w,2);
netconfig.layersizes = {};
for d =1:numel(stack)
netconfig.layersizes =[netconfig.layersizes ; size(stack{d}.w,1)];
end
end
end
end
(7) initializeNet
function stack = initializeNet(netsize)
layersize=length(netsize(:));
stack = cell(layersize-1,1);
for l=1:layersize-1
hiddenSize=netsize(l+1);
visibleSize=netsize(l);
r =sqrt(6) /sqrt(hiddenSize+visibleSize+1);
rand('state',2)
stack{l}.w= rand(hiddenSize, visibleSize) *2 * r - r; stack{l}.b= zeros(hiddenSize, 1);
end
end
(8) 运行结果
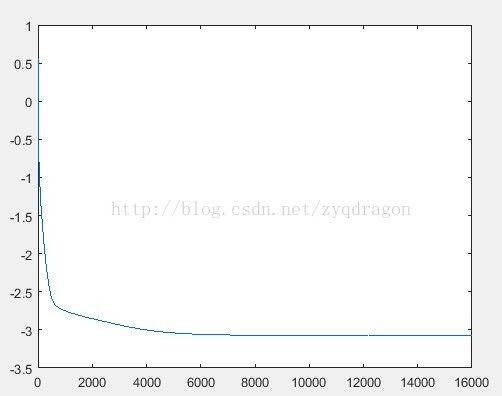
深度网络收敛,运行结果如下图所示:
(F1)
输出标签值如下:
v_groundTruth =
0.2000 0.3000 1.0000 0.8000
1.1000 0.8000 1.8000 1.2000
深度网络实际拟合值如下:
v_M =
0.2001 0.3001 0.9999 0.7999
1.0999 0.8000 1.7999 1.2000
由上面数据比较可见,两者差距较小,深度网络较好地拟合。
3. 多样本深度网络欠拟合代码
本例在第2部分中的四组样本的基础上,增加一组样本,深度网络无法拟合。网络参数为:
netsize=[inputsize,5,6,8,7,5,4];
(1) Main_function
clear all
clc
close all
TrainData=[1 2 3 4 5 6 7 8 9 10
1 9 17 25 33 41 49 57 65 73];
batchsize=5;
TrainData=TrainData(:,1:batchsize);
TrainLabel=[1 0.3 0.8 0.2 0.67;
1.8 0.8 1.2 1.1 0.18];
classnum=2;%输出端数目
%获取数据的维度
inputsize=size(TrainData,1);
%获取数据的数量
datanum=size(TrainData,2);
% 用一个向量来定义网络的深度,以及每层神经元数目。
netsize=[inputsize,5,6,8,7,5,4];
% netsize=[inputsize,5,6,8,9,9,8,7,5,4];
%网络最后一层神经元数数目,再考虑一个偏置。
lastsize=netsize(end)+1;
%初始化网络参数,以结构体的形式保存。
stack =initializeNet(netsize);
% 在训练时,往往需要将参数转成一列向量,提供给损失函数。
% stack->stackTheta,netconfig保存一些结构参数。
[stackTheta,netconfig] = stack2params(stack);
% 指定固定的最后一层的初始化的值;
rand('state',2)
lastTheta =0.0005 * randn(lastsize * classnum, 1);
%最终网络需要的参数
Theta=[lastTheta ; stackTheta ];
%lastTheta表示深度网络最后一层的权值
% the followingpart is for the traing epoch.
% batchsize=5;
%%每次训练的小批量样本数
batchnum=floor(size(TrainData,2)/batchsize);
DataNum=size(TrainData,2);
alpha=1e-2;
%这是学习率,一般随着网络的悬念都需要不断的减小
lambda = 1e-4; %Weight decay parameter
forepoch=1:16000
v_epoch=epoch
if epoch>=16000
alpha=1e-3;
end
idx=randperm(DataNum);
for t=1:batchnum
subdata=TrainData(:,idx((t-1)*batchsize+1:(t)*batchsize));
sublabel=TrainLabel(:,idx((t-1)*batchsize+1:(t)*batchsize));
[cost(epoch),grad]=ReLUDNNCost(Theta,classnum,lastsize,netconfig,lambda,subdata,sublabel);
Theta=Theta-alpha*grad;
end
end
plot(log(cost))
(2) 运行结果
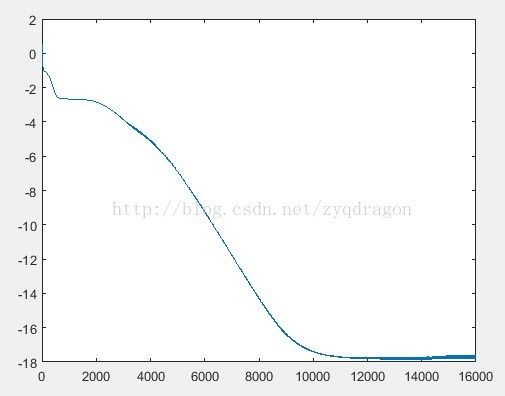
深度网络无法很好地收敛,运行结果如下图所示:
(F2)
输出标签值如下:
v_groundTruth =
0.6700 0.3000 0.2000 1.0000 0.8000
0.1800 0.8000 1.1000 1.8000 1.2000
深度网络实际输出值如下
v_M =
0.6114 0.4340 0.4819 0.9996 0.4429
0.1749 0.8124 1.1275 1.8001 1.1651
由上面数据比较可见,两者差距较大,深度网络无法很好地拟合。
4. 加深网络后多样本可以很好地拟合
本例在第3部分中的五组样本,深度网络无法拟合的情况下,加深网络深度,网络参数为:
netsize=[inputsize,5,6,8,9,9,8,7,5,4]; 深度网络很好地拟合。
(1) Main_function
clear all
clc
close all
TrainData =[1 2 3 4 5 6 7 8 9 10
1 9 17 25 33 41 49 57 65 73];
% TrainData=TrainData(:,1:6);
% TrainLabel=[1 0.3 1.8 0.87 0.66 0.83];
% batchsize=6;
% classnum=1;%输出端数目
batchsize=5;
TrainData=TrainData(:,1:batchsize);
TrainLabel=[1 0.3 0.8 0.2 0.67;
1.8 0.8 1.2 1.1 0.18];
% TrainLabel=[1 0.3 0.8 0.2;
% 1.8 0.8 1.2 1.1];
classnum=2;%输出端数目
%获取数据的维度
inputsize=size(TrainData ,1);
%获取数据的数量
datanum=size(TrainData ,2);
% 用一个向量来定义网络的深度,以及每层神经元数目。
netsize=[inputsize,5,6,8,9,9,8,7,5,4];
%网络最后一层神经元数数目,再考虑一个偏置。
lastsize=netsize(end)+1;
%初始化网络参数,以结构体的形式保存。
stack = initializeNet(netsize);
% 在训练时,往往需要将参数转成一列向量,提供给损失函数。
% stack ->stackTheta,netconfig保存一些结构参数。
[stackTheta, netconfig] =stack2params(stack);
% 指定固定的最后一层的初始化的值;
rand('state',2)
lastTheta = 0.0005 * randn(lastsize *classnum, 1);
%最终网络需要的参数
Theta=[ lastTheta ; stackTheta ];
%lastTheta表示深度网络最后一层的权值
% the following part is for the traing epoch.
% batchsize=5;
%%每次训练的小批量样本数
batchnum=floor(size(TrainData,2)/batchsize);
DataNum=size(TrainData,2);
alpha=1e-2;
%这是学习率,一般随着网络的悬念都需要不断的减小
lambda = 1e-4; % Weight decay parameter
for epoch=1:16000
v_epoch=epoch
if epoch>=16000
alpha=1e-3;
end
idx=randperm(DataNum);
for t=1:batchnum
subdata=TrainData(:,idx((t-1)*batchsize+1:(t)*batchsize));
sublabel=TrainLabel(:,idx((t-1)*batchsize+1:(t)*batchsize));
[cost(epoch),grad]=ReLUDNNCost(Theta,classnum,lastsize,netconfig,lambda,subdata,sublabel);
Theta=Theta-alpha*grad;
end
end
plot(log(cost))
(2) 运行结果
深度网络很好地收敛,运行结果如下图所示:
(F3)
输出标签值如下:
v_groundTruth =
0.6700 0.3000 0.2000 1.0000 0.8000
0.1800 0.8000 1.1000 1.8000 1.2000
深度网络实际输出值如下:
v_M =
0.6699 0.3000 0.2002 0.9999 0.7999
0.1800 0.8000 1.0999 1.7998 1.2001
由上面数据比较可见,两者差距较小,深度网络很好地拟合。
5. 总结
从第2部分至第5部分的训练样本及运行结果可以看出,当深度网络较浅时,可能会面临多样本数据无法很好拟合的情况。此时,如果加深网络层数,则可能会使得网络很好地拟合多组训练样本。