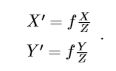《第5讲 相机与图像 》读书笔记

本文是《视觉SLAM十四讲》第5讲的个人读书笔记，为防止后期记忆遗忘写的。

本讲讨论的是“机器人如何观测外部世界”， 也就是观测方程部分。而在以相机为主的视觉 SLAM 中，观测主要是指相机成像的过程。 

本节目标

1. 总结针孔相机的模型、内参与径向畸变参数。
2. 总结世界坐标-->相机坐标-->物理成像面坐标-->归一化成像坐标---->畸变纠正坐标 的变换。
3. 学习并总结点云拼接程序。

5.1 相机模型

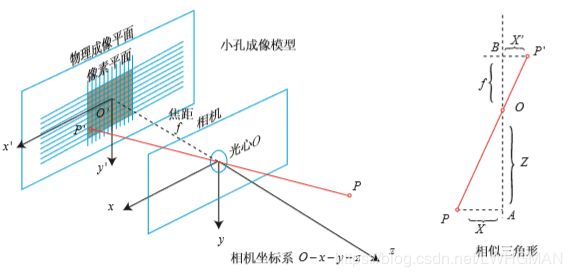
针孔模型描述相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程 。由于 相机镜头上的透镜的存在，会使得光线投影到成像平面的过程中会产生畸变。因此，我们 使用针孔和畸变两个模型来描述整个投影过程。 这两个模型能够 把外部的三维点投影到相机内部成像平面，构成了相机的内参数。

在物理成像方面（讨论的是物理面）：设 2观测坐标P（以自己的位姿为标准） 的坐标为 [X,Y,Z]T，P′ 为 [X′,Y ′,Z′]T。

   <=======>

上式只是描述了点 P 和它的像之间的空间关系。不过，在相机中，我们最终获得的是 一个个的像素，这期间还将进行一些变化。

为了描述传感器将感受到的光 线转换成图像像素的过程，我们设在物理成像平面上固定着一个像素平面 o−u−v。我们在像素平面得到了 P′ 的 4像素坐标：[u,v]T。4像素坐标系与3成像平面坐标之间，相差了一个缩放和一个原点的平移。我 们设像素坐标在 u 轴上缩放了 α 倍，在 v 上缩放了 β 倍。同时，原点平移了 [cx,cy]T。那 么，3成像平面坐标P′ 的坐标与4像素坐标系坐标 [u,v]T 的关系为： 

由于相机在运动，所以 2观测坐标P的相机坐标应该是它的1世界坐标（记为 Pw）， 根据相机的当前位姿，变换到相机坐标系下的结果。相机的位姿由它的旋转矩阵 R 和平移向量 t 来描述。。相机的位姿 R,t 又称为相机的外参数 （CameraExtrinsics）。相比于不变的内参，外参会随着相机运动发生改变，同时也是 SLAM 中待估计的目标，代表着机器人的轨迹。 像素坐标 [u,v]T，看成对归一化平面上的点进行量化测量的结果。 从而给出了世界坐标到像素坐标的变化数学关系。

上式两侧都是齐次坐标。因为齐次坐标乘上非零常数后表达同样的含义，所以可以简 单地把 Z 去掉：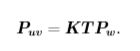                                                                                                        

---

但是，因为透镜等原因，相机成像会发生畸变。。径向畸变可看成 坐标点沿着长度方向发生了变化 δr, 也就是其距离原点的长度发生了变化。切向畸变可以 看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化 δθ。 

对于径向畸变的纠正，其中 [x,y]T 是未纠正的点的坐标，[xcorrected,ycorrected]T 是纠正后的点的坐标，注意它们 都是归一化平面上的点，而不是像素平面上的点。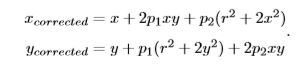                                                                                                                                                                          

对于切向畸变，可以使用另外的两个参数 p1,p2 来进行纠正: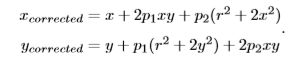                                                                                                                                                  

所以，对于相机坐标系中的一点 P(X,Y,Z)，我们能够通过五个畸变系数找到这个点在像素平面上的正确位置。

归一平面是对物理成像平面进行除以Z进行归一化的3成像平面坐标。

最后，我们小结一下单目相机的成像过程：

       

第3步和第4步间还得插入一个相机畸变纠正的变化过程。

---

双目相机模型

仅根据一个像素，我们是无法确定 这个空间点的具体位置的。这是因为，从相机光心到归一化平面连线上的所有点，都可以 投影至该像素上。只有当 P 的深度确定时（比如通过双目或 RGB-D 相机），我们才能确 切地知道它的空间位置。

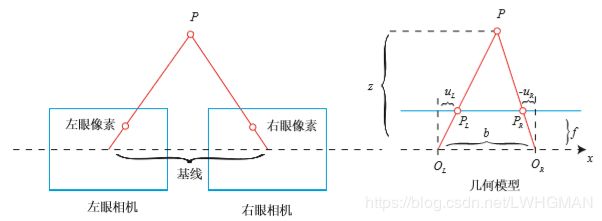
在左右双目的相机中，我们可以把两个相机都看 作针孔相机。它们是水平放置的，意味两个相机的光圈中心都位于 x 轴上。它们的距离称 为双目相机的基线（Baseline, 记作 b），是双目的重要参数。

  

。根据三角形 P−PL−PR 和 P−OL−OR 的相似关系，有：。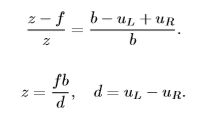

---

RGB-D 相机模型 

RGB-D 相机的做法更为“主动”一些，它 能够主动测量每个像素的深度。目前的 RGB-D 相机按原理可分为两大类：通过红外结构光、通过飞行时间法。无论是结构光还是 ToF，RGB-D 相机都需要向探测目标发射一束光线（通常是红外 光）。

在测量深度之后，RGB-D 相机通常按照生产时的各个相机摆放位置，自己完成深度 与彩色图像素之间的配对，输出一一对应的彩色图和深度图。我们可以在同一个图像位置， 读取到色彩信息和距离信息，计算像素的 3D 相机坐标，生成点云（Point Cloud）。

但是，由于这种发射-接受的测量方 式，使得它使用范围比较受限。用红外进行深度值测量的 RGB-D 相机，容易受到日光或 其他传感器发射的红外光干扰，因此不能在室外使用，同时使用多个时也会相互干扰。对 于透射材质的物体，因为接受不到反射光，所以无法测量这些点的位置。此外，RGB-D 相 机在成本、功耗方面，都有一些劣势。 

---

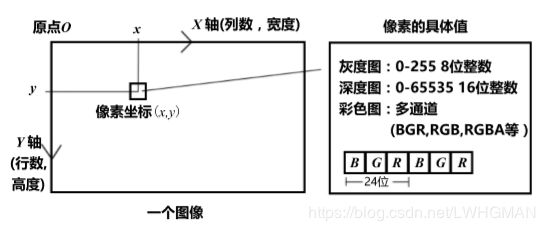
5.2 图像

                                         

我们平时说的图 像的宽度和列数，对应着 X 轴；而图像的行数或高度，则对应着它的 Y 轴。 unsigned char pixel = image[y][x];

---

5.4 实践：拼接点云

                                                                                                                                                                                                    

本节程序提供了五张 RGB-D 图像，并且知道了每个图像的内参和外参。根据 RGB-D 图像和相机内参，我们可以计算任何一个像素在相机坐标系下的位置。同时，根据相机位姿，又能计算这些像素在世界坐标系下的 位置。如果把所有像素的空间坐标都求出来，相当于构建一张类似于地图的东西。

在 color/下有 1.png 到 5.png 五张 RGB 图，而在 depth/下有五张对应的深度图。同时，pose.txt 文件给出了五张图像 的相机位姿（以 Twc 形式）。位姿记录的形式是平移向量加旋转四元数：[x,y,z,qx,qy,qz,qw]。

#include 
#include 
#include   // for formating strings
#include 
#include 
#include  
#include  
#include  
#include 
using namespace std;

int main( int argc, char** argv )
{
    vector colorImgs, depthImgs;    // 彩色图和深度图.
    vector poses;         // 相机位姿,Isometry3d实质上是4＊4的矩阵.
    
    ifstream fin("./pose.txt");
    if (!fin)
    {
        cerr<<"请在有pose.txt的目录下运行此程序"<>d;
        Eigen::Quaterniond q( data[6], data[3], data[4], data[5] );     //Quaterniond,四元数,(qw,qx,qy,qz)
        Eigen::Isometry3d T(q);
        T.pretranslate( Eigen::Vector3d( data[0], data[1], data[2] ));  //生成变换矩阵
        poses.push_back( T );
    }
    
    // 计算点云并拼接
    // 相机内参  U=fx*Xcorrected+cx       V=fy*Ycorrected+cy
    double cx = 325.5;
    double cy = 253.5;
    double fx = 518.0;
    double fy = 519.0;
    double depthScale = 1000.0;
    
    cout<<"正在将图像转换为点云..."< PointCloud;
    
    // 新建一个点云
    PointCloud::Ptr pointCloud( new PointCloud ); 
    for ( int i=0; i<5; i++ )
    {
        cout<<"转换图像中: "< ( v )[u]; // 深度值
                if ( d==0 ) continue;                                // 为0表示没有测量到
                Eigen::Vector3d point; 
        
        //U=fx*Xcorrected+cx   V=fy*Ycorrected+cy  fx= α*f   fy= β*f 
        //求相机坐标系坐标point,并转换成世界坐标系坐标pointWorld
                point[2] = double(d)/depthScale; 
                point[0] = (u-cx)*point[2]/fx;
                point[1] = (v-cy)*point[2]/fy; 
                Eigen::Vector3d pointWorld = T*point;
        //绘制点云  
                PointT p ;
                p.x = pointWorld[0];
                p.y = pointWorld[1];
                p.z = pointWorld[2];
                p.b = color.data[ v*color.step+u*color.channels() ];
                p.g = color.data[ v*color.step+u*color.channels()+1 ];
                p.r = color.data[ v*color.step+u*color.channels()+2 ];
                pointCloud->points.push_back( p );
            }
    }
    
    pointCloud->is_dense = false;
    cout<<"点云共有"<size()<<"个点."<