深度学习入门笔记(十二):权重初始化
专栏——深度学习入门笔记
声明
1)该文章整理自网上的大牛和机器学习专家无私奉献的资料,具体引用的资料请看参考文献。
2)本文仅供学术交流,非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益,还望海涵,并联系博主删除。
3)博主才疏学浅,文中如有不当之处,请各位指出,共同进步,谢谢。
4)此属于第一版本,若有错误,还需继续修正与增删。还望大家多多指点。大家都共享一点点,一起为祖国科研的推进添砖加瓦。
文章目录
- 专栏——深度学习入门笔记
- 声明
- 深度学习入门笔记(十二):深入理解梯度
- 1、梯度消失/梯度爆炸
- 2、神经网络的权重初始化
- 1_对w随机初始化
- 2_Xavier初始化
- 3_He初始化
- 3、TensorFlow实现权重初始化
- 1_常量初始化
- 2_正态分布初始化
- 3_均匀分布初始化
- 4_截断正态分布初始化
- 5_正交矩阵初始化
- 6_Xavier初始化、He_初始化
- 4、总结
- 推荐阅读
- 参考文章
深度学习入门笔记(十二):深入理解梯度
1、梯度消失/梯度爆炸
早些时间写过一个博客——深度学习100问之深入理解Vanishing/Exploding Gradient(梯度消失/爆炸),感兴趣的小伙伴可以看一下。
训练神经网络,尤其是深度神经网络所面临的一个问题就是 梯度消失或梯度爆炸,那么什么是 梯度消失或梯度爆炸?
其实就是训练神经网络时,导数或坡度 有时会变得非常大,或者非常小,甚至于以指数方式变小,这加大了训练的难度。下面通过一个例子来详细的讲解:
假设正在训练这样一个 极深 的神经网络,为了简化问题,假设神经网络每层只有两个隐藏单元,但是因为 极深,所以还有很多参数,如 W [ 1 ] W^{[1]} W[1], W [ 2 ] W^{[2]} W[2], W [ 3 ] W^{[3]} W[3] 等等,直到 W [ l ] W^{[l]} W[l]。为了简单起见,假设使用线性激活函数 g ( z ) = z g(z)=z g(z)=z,同时忽略偏置 b b b,即假设 b [ l ] b^{[l]} b[l]=0,这样的话,输出:
y = W [ l ] W [ L − 1 ] W [ L − 2 ] … W [ 3 ] W [ 2 ] W [ 1 ] x y=W^{[l]}W^{[L -1]}W^{[L - 2]}\ldots W^{[3]}W^{[2]}W^{[1]}x y=W[l]W[L−1]W[L−2]…W[3]W[2]W[1]x
如果你是数学帕金森患者或者想考验我的数学水平,那么就简单说一下推导过程:
根据前向传播中的公式 W [ 1 ] x = z [ 1 ] W^{[1]} x = z^{[1]} W[1]x=z[1],又因为 b = 0 b=0 b=0,所以 z [ 1 ] = W [ 1 ] x z^{[1]} =W^{[1]} x z[1]=W[1]x, a [ 1 ] = g ( z [ 1 ] ) a^{[1]} = g(z^{[1]}) a[1]=g(z[1]),而由于使用的事线性激活函数 g ( z ) = z g(z)=z g(z)=z,所以第一项 W [ 1 ] x = a [ 1 ] W^{[1]} x = a^{[1]} W[1]x=a[1],通过推理。。。得出 W [ 2 ] W [ 1 ] x = a [ 2 ] W^{[2]}W^{[1]}x =a^{[2]} W[2]W[1]x=a[2],因为 a [ 2 ] = g ( z [ 2 ] ) = g ( W [ 2 ] a [ 1 ] ) a^{[2]} = g(z^{[2]})=g(W^{[2]}a^{[1]}) a[2]=g(z[2])=g(W[2]a[1]),第一项 W [ 1 ] x = a [ 1 ] W^{[1]} x = a^{[1]} W[1]x=a[1],故可以用 W [ 1 ] x W^{[1]}x W[1]x 替换 a [ 1 ] a^{[1]} a[1],所以 a [ 2 ] = g ( W [ 2 ] W [ 1 ] x ) = W [ 2 ] W [ 1 ] x a^{[2]}=g(W^{[2]}W^{[1]}x)=W^{[2]}W^{[1]}x a[2]=g(W[2]W[1]x)=W[2]W[1]x。依次类推,可得 a [ l ] = W [ l ] W [ L − 1 ] W [ L − 2 ] … W [ 3 ] W [ 2 ] W [ 1 ] x a^{[l]}=W^{[l]}W^{[L -1]}W^{[L - 2]}\ldots W^{[3]}W^{[2]}W^{[1]}x a[l]=W[l]W[L−1]W[L−2]…W[3]W[2]W[1]x。
吴恩达老师手稿如下:
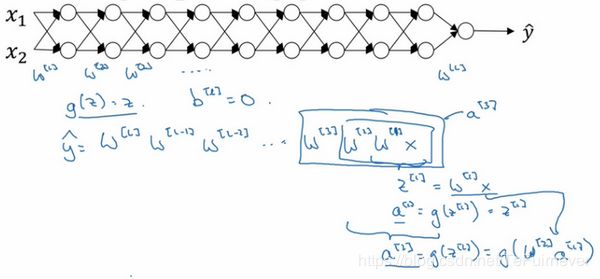
假设每个权重矩阵 W [ l ] = [ 1.5 0 0 1.5 ] W^{[l]} = \begin{bmatrix} 1.5 & 0 \\0 & 1.5 \\\end{bmatrix} W[l]=[1.5001.5],从技术上来讲,最后一项有不同维度,可能它就是余下的权重矩阵,比如这里就是(None,1),所以根据上面推导的公式,可以得到 y = W [ L ] [ 1.5 0 0 1.5 ] ( L − 1 ) x y= W^{[L]}\begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \\\end{bmatrix}^{(L -1)}x y=W[L][1.5001.5](L−1)x。又因为 [ 1.5 0 0 1.5 ] = 1.5 ∗ [ 1 0 0 1 ] \begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \\\end{bmatrix} = 1.5 * \begin{bmatrix} 1 & 0 \\ 0 & 1 \\\end{bmatrix} [1.5001.5]=1.5∗[1001],是1.5倍的单位矩阵(注意:网络的输出是 y ^ \hat y y^ 而不是 y y y),所以计算结果是 y ^ = 1.5 ( L − 1 ) x \hat{y}={1.5}^{(L-1)}x y^=1.5(L−1)x。
如果对于一个深度神经网络来说,它的 L L L 值明显较大,那么 y ^ \hat{y} y^ 的值也会非常大。在数学上分析的话,实际上它就是一个指数函数,因此是呈指数级增长的。该函数的增长比率是 1.5 1.5 1.5,其实就是 1. 5 L 1.5^L 1.5L,相当于下图中 a > 1 a>1 a>1 的情况,是爆炸式增长的趋势。因此对于一个深度神经网络,输出值将爆炸式增长。

相反的,如果权重是 0.5 0.5 0.5,即 W [ l ] = [ 0.5 0 0 0.5 ] W^{[l]} = \begin{bmatrix} 0.5& 0 \\ 0 & 0.5 \\ \end{bmatrix} W[l]=[0.5000.5],这项也就变成了 0.5 L {0.5}^{L} 0.5L,矩阵 y = W [ L ] [ 0.5 0 0 0.5 ] ( L − 1 ) x y= W^{[L]}\begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \\\end{bmatrix}^{(L - 1)}x y=W[L][0.5000.5](L−1)x,再次忽略 W [ L ] W^{[L]} W[L],因此每个矩阵都小于1,相当于上图中 0 < a < 1 0

小结一下,直观理解上,分两种情况:
- 权重 W W W 只比1略大一点,可能是 [ 0.9 0 0 0.9 ] \begin{bmatrix}0.9 & 0 \\ 0 & 0.9 \\ \end{bmatrix} [0.9000.9],深度神经网络的激活函数将爆炸式增长;
- 权重 W W W 只比1略小一点,可能是 [ 1.1 0 0 1.1 ] \begin{bmatrix}1.1 & 0 \\ 0 & 1.1 \\ \end{bmatrix} [1.1001.1],深度神经网络的激活函数将爆炸式减小。
在深度神经网络中,激活函数与 L L L 呈指数级增长或呈指数递减,在这样一个深度神经网络中,如果梯度函数也与 L L L 相关的指数增长或递减,它们的值将会变得极大或极小,从而导致训练难度上升,尤其是梯度指数小于 L L L 时,梯度下降算法的步长会非常非常小,梯度下降算法将花费很长时间来学习。在很长一段时间内,它曾是训练深度神经网络的阻力,虽然有一个不能彻底解决此问题的解决方案,但是还是有一些方法可以提供帮助。
2、神经网络的权重初始化
针对深度神经网络产生梯度消失和梯度爆炸的问题,我们想出了一个不完整的解决方案,虽然不能彻底解决问题,却很有用,即为神经网络更谨慎地选择随机初始化参数。除此之外,初始化还对模型的收敛速度和性能有着至关重要的影响,因为说白了,神经网络其实就是对权重参数 w 的不停迭代更新,以期达到较好的性能。
那么神经元初始化的方式有哪些?
1_对w随机初始化
目前最常使用的就是随机初始化权重,比如常数初始化、正态分布初始化、均匀分布初始化、截断正态分布初始化、正交矩阵初始化等等。然而这是有弊端的,一旦随机分布选择不当,就会导致网络优化陷入困境,所以很多时候是调参去解决这个问题,避免陷入局部最优,会出现损失函数不收敛等情况。
首先创建了一个10层的神经网络,非线性变换为 tanh,每一层的参数都是随机正态分布。
W = tf.Variable(np.random.randn(node_in, node_out))
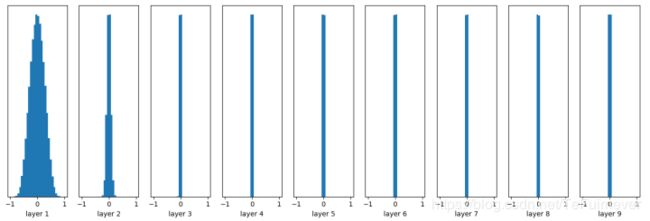
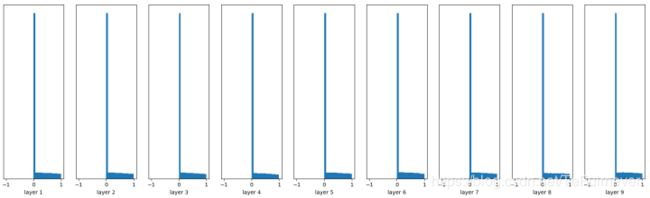
随着层数的增加,输出值迅速向0靠拢,在后几层中,几乎所有的输出值 x 都很接近0!根据反向传播算法的链式法则,梯度等于当前函数的梯度乘以后一层的梯度,这意味着输出值是计算梯度的一个乘法因子,输出值接近于0将直接导致梯度很小,使得参数难以被更新。如果把初始值调大一些:W = tf.Variable(np.random.randn(node_in, node_out))。

几乎所有的值集中在-1或1附近,神经元saturated了!注意到tanh在-1和1附近的梯度都接近0,这同样导致了梯度太小,参数难以被更新。
2_Xavier初始化
论文地址:Understanding the difficulty of training deep feedforward neural networks
Xavier 初始化可以解决上面的问题!其初始化方式也并不复杂,保持输入和输出的方差一致,这样就避免了所有输出值都趋向于0。
W = tf.Variable(np.random.randn(node_in, node_out)) / np.sqrt(node_in)
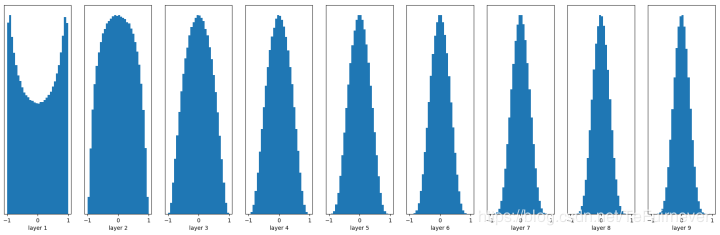
不过在应用 RELU 激活函数时:

后面的趋势却是越来越接近0。。。
3_He初始化
论文地址:Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
He 初始化的思想是:在 ReLU 网络中,假定每一层有一半的神经元被激活,另一半为0,所以,要保持 variance 不变,只需要在 Xavier 的基础上再除以2。
W = tf.Variable(np.random.randn(node_in,node_out)) / np.sqrt(node_in/2)
3、TensorFlow实现权重初始化
1_常量初始化
x = tf.get_variable('x', shape, initializer=tf.constant_initializer(1))
2_正态分布初始化
x = tf.get_variable('x', shape,
initializer=tf.random_normal_initializer(
mean=0.0,
stddev=1.0,
seed=None,
dtype=tf.float32))
y = tf.get_variable('y', shape,
initializer=tf.truncated_normal_initializer(
mean=0.0,
stddev=1.0,
seed=None,
dtype=tf.float32))
3_均匀分布初始化
x = tf.get_variable('x', shape,
initializer=tf.random_uniform_initializer(
minval=0,
maxval=10,
seed=None,
dtype=tf.float32))
# 或
x = tf.get_variable('x', shape,
initializer=tf.uniform_unit_scaling_initializer(
factor=1.0,
seed=None,
dtype=tf.float32))
4_截断正态分布初始化
x = tf.get_variable('x', shape,
initializer=tf.truncated_normal_initializer(
mean=0.0,
stddev=1.0,
seed=None,
dtype=tf.float32))
5_正交矩阵初始化
x = tf.get_variable('x', shape,
initializer=tf.orthogonal_initializer(
gain=1.0,
seed=None,
dtype=tf.float32))
6_Xavier初始化、He_初始化
在上面给出了具体的代码,还有:
tf.glorot_uniform_initializer()
# 或
tf.glorot_normal_initializer()
4、总结
RELU 激活函数初始化推荐使用 He 初始化,tanh 初始化推荐使用 Xavier 初始化。
不过我个人目前用的比较多的是截断正态分布初始化,其他也都有在用,但是提升不是太明显,需要尝试才能确定针对不同问题时是不是能有效的提升,也可能是因为专业不是前端精密行业,还是需要斟酌。
推荐阅读
- 深度学习入门笔记(一):深度学习引言
- 深度学习入门笔记(二):神经网络基础
- 深度学习入门笔记(三):求导和计算图
- 深度学习入门笔记(四):向量化
- 深度学习入门笔记(五):神经网络的编程基础
- 深度学习入门笔记(六):浅层神经网络
- 深度学习入门笔记(七):深层神经网络
- 深度学习入门笔记(八):深层网络的原理
- 深度学习入门笔记(九):深度学习数据处理
- 深度学习入门笔记(十):正则化
- 深度学习入门笔记(十一):深度学习数据读取
- 深度学习入门笔记(十二):权重初始化
参考文章
- 吴恩达——《神经网络和深度学习》视频课程
- https://zhuanlan.zhihu.com/p/25110150