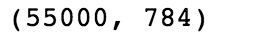TensorFlow实战3：实现Logistic回归小例子

解决分类问题里最普遍的baseline model就是逻辑回归，简单同时可解释性好，使得它大受欢迎，我们来用tensorflow完成这个模型的搭建。
在这篇文章中我们使用的是MNIST手写数字识别图像的数据集。
模型搭建的步骤和代码如下：

0.环境设定
导入一些必要的包

import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import time

1.数据读取

#使用tensorflow自带的工具来加载MNIST手写数字集合
mnist = input_data.read_data_sets('./data/mnist', one_hot=True) 

上图即表示数据读取加载完成，后面我们可以查看一下数据的基本信息。

#查看一下数据维度
mnist.train.images.shape

#查看target维度
mnist.train.labels.shape

2.准备好placeholder，开好容器来装数据

batch_size = 128     #指定每次传入进内存的数据大小，指定之后可以防止数据出现错误
X = tf.placeholder(tf.float32, [batch_size, 784], name='X_placeholder') 
Y = tf.placeholder(tf.int32, [batch_size, 10], name='Y_placeholder')

#其实可以用下面这种方式，在不知道数据集大小的时候，传入的数据大小不固定，后面再根据实际情况来指定
# X = tf.placeholder(tf.float32, [None, 784], name='X_placeholder') 
# Y = tf.placeholder(tf.int32, [None, 10], name='Y_placeholder')

3.准备好参数/权重
此处准备参数时一定要将参数的维度设定好，不然后面的计算会出错误。

w = tf.Variable(tf.random_normal(shape=[784, 10], stddev=0.01), name='weights')
b = tf.Variable(tf.zeros([1, 10]), name="bias")

4.拿到每个类别的score
此处通过矩阵运算，得到的只是每个类别的得分，但并没有归一化到概率。

logits = tf.matmul(X, w) + b   

5.计算多分类softmax的loss function

# 求交叉熵损失
entropy = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y, name='loss')
# 求平均
loss = tf.reduce_mean(entropy)    #此处使用的是求平均值的方式

6.准备好optimizer

这里的最优化用的是随机梯度下降，我们可以选择AdamOptimizer这样的优化器。Adam.Optimiter()是一个带动量的梯度下降，不会很快陷到局部最低点，它会找到一个接近全局最优解的低点，但不保证会找到全局最优解.

learning_rate = 0.01
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss)

7.在session里执行graph里定义的运算

#迭代总轮次
n_epochs = 30

with tf.Session() as sess:
    # 在Tensorboard里可以看到图的结构
    writer = tf.summary.FileWriter('./graphs/logistic_reg', sess.graph)

    start_time = time.time()
    sess.run(tf.global_variables_initializer()) 
    n_batches = int(mnist.train.num_examples/batch_size)
    for i in range(n_epochs): # 将所有的训练数据迭代这么多轮
        total_loss = 0

        for _ in range(n_batches):
            X_batch, Y_batch = mnist.train.next_batch(batch_size)
            _, loss_batch = sess.run([optimizer, loss], feed_dict={X: X_batch, Y:Y_batch}) 
            total_loss += loss_batch
        print('Average loss epoch {0}: {1}'.format(i, total_loss/n_batches))

    print('Total time: {0} seconds'.format(time.time() - start_time))

    print('Optimization Finished!')

由于此数据集有测试集，不同于上面两篇文章中自己生成的数据，因此需要用测试集来测试模型的准确率。

    # 测试模型，也需要放到session里面来运行。

    preds = tf.nn.softmax(logits)   #通过softmax()来计算每个样本类别的概率值
    correct_preds = tf.equal(tf.argmax(preds, 1), tf.argmax(Y, 1))   #此处得出的是一个一阶张量，由一串0，1数字组成，表示的是每个样本是否预测预测准确
    accuracy = tf.reduce_sum(tf.cast(correct_preds, tf.float32))  #对预测是否准确的列表求平均值 ，cast()函数是将整型数据转化为浮点型数据   

    n_batches = int(mnist.test.num_examples/batch_size) #输入数据的批次
    total_correct_preds = 0

    #对测试集每个batch求accuracy
    for i in range(n_batches):
        X_batch, Y_batch = mnist.test.next_batch(batch_size)    #此处是从测试集中按批次的输入数据
        accuracy_batch = sess.run([accuracy], feed_dict={X: X_batch, Y:Y_batch}) 
        total_correct_preds += accuracy_batch[0]
    #对每个batch求平均值
    print('Accuracy {0}'.format(total_correct_preds/mnist.test.num_examples))

    writer.close()

经过30轮的迭代之后，打印结果如下：

又图可知训练的分类模型在测试集上面的准确率为0.9165，这个准确率相对而言还比较低，可以通过调整参数来取得模型准确率的进一步提升。