颜值估计（2）

版权声明：本篇文章为博主原创文章，码字不易，未经博主允许，不得转载：https://mp.csdn.net/postedit/80164870

本文为2015年论文《A NEW HUMANLIKE FACIAL ATTRACTIVENESS PREDICTOR WITH CASCADED

FINE-TUNING DEEP LEARNING MODEL 》的解读（点我下载）。

该论文所用的方法主要对原始图像进行了预处理，使得最终精度得到了很大程度的提升。

以往的研究中，很多基于神经网络的方法都是针对原始RGB图像进行特征提取，通过分类、回归、或者分类+回归的方式对结果进行预测。而预测方式又可以分为针对特定标签进行分类/预测与针对标签分布进行学习的方法。

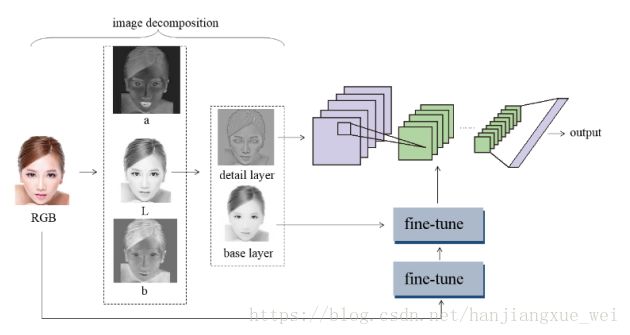
该论文中，作者受到心理学研究的启发，由于人类对人脸面部平滑度，颜色信息以及光照信息等比较敏感，因此可以通过颜色空间转换，将原始RGB图像转换到Lab颜色空间（点我查看）从而获得这些信息。在Lab空间中，L分量只控制明暗程度，a和b分量分别控制不同的颜色信息。这样就可以将原始图像转化为与人类视觉感知相一致的图像，从而能够更贴近人类视觉行为。然后对L分量进行保边滤波，从而获得图像的平滑层与细节层信息（低频与高频信息），这样便提取出了图像的平滑度信息。综合而言，算法通过对原始图像的一系列预处理，获得了人脸平滑度、颜色、光照信息等，这点与心理学研究的结果较为契合。最后在对获得的各种信息进行特征提取过程，利用神经网络对年龄进行回归，并利用皮尔逊相关（点我查看）进行准确性判定。方法较为新颖，而且得到的精度有了很大的提升。

传统的特征提取方式针对人脸年龄评估相比较神经网络而言，其效果十分有限，而且由于侧重点不同，往往传统的手工特征提取过程容易丢掉部分信息，导致评估结果并不是十分高。而神经网络，大家都知道，其在特征提取方式上面拥有很大的优势，这方面的比较，可以通过很多论文得到验证，在此不再进行赘述。

-------------------------------------------------------------------------------------------------------------------------

算法使用的数据集为SCUT-FBP，流程图如下：

算法具体有一下几个步骤：

一、颜色空间转换

这块知识在一般的图像处理书上讲解较少，大部分颜色空间转换都集中在RGB->XYZ， RGB->CMY/CMYK， RGB->HSI上面。而将RGB->Lab空间方面的介绍却比较少，上网查了很多博客，针对这方面处理也有部分讲解，一般来讲可以通过将RGB图像先转换到XYZ颜色空间，然后再将XYZ空间的结果转换到Lab空间。可以参考一下：（点我打开）。这里本人根据其c++代码编写了了一个python的实现代码，希望可以帮到有需要的朋友。

#coding=utf-8
from PIL import Image
import numpy as np
import os
import math

#原始图像路径
image_path = r'\图像地址\'
rows, cols, channels = 224, 224, 1

def gamma(im_channel):
    return ((im_channel+0.055)/1.055)**2.4 if im_channel > 0.04045 else im_channel / 12.92

def f(im_channel):
    return im_channel**1/3 if im_channel > 0.008856 else 7.787 * im_channel + 0.137931

def convert_image(image_path, rows,cols, channels,  mode):
    #读入图像
    imgs = os.listdir(image_path)
    num = len(imgs)
    #创建保存结果的矩阵
    L_ = np.zeros((num, rows, cols, channels), dtype=np.float32)   
    a_ = np.zeros((num, rows, cols, channels), dtype=np.float32)
    b_ = np.zeros((num, rows, cols, channels), dtype=np.float32)
    for i in range(num):
        img = Image.open(im)

        #resize到想要的大小

        img = img.resize((rows, cols))
        #获取像素
        pix = img.load()
        for x in range(rows):
            for y in range(cols):
                # 获得三个通道值
                r, g, b = pix[x, y]

                #伽马映射
                R = gamma(r/255.0)
                G = gamma(g/255.0)
                B = gamma(b/255.0)
                #转换到XYZ空间
                X = 0.412453 * R + 0.357580 * G + 0.180423 * B
                Y = 0.212671 * R + 0.715160 * G + 0.072169 * B
                Z = 0.019334 * R + 0.119193 * G + 0.950227 * B
                #对XYZ空间进行归一化
                X /= 0.95047
                Y /= 1.0
                Z /= 1.08883

                #对XYZ空间进行映射
                FX = f(X)
                FY = f(Y)
                FZ = f(Z)
                #转换到Lab空间               
                L_[i, x, y, channel] = 116 * FY - 16 if Y > 0.008856 else 903.3 * Y          
                a_[i, x, y, channel] = 500 * (FX - FY)
                b_[i, x, y, channel] = 200 * (FY - FZ)

当然，我们其实可以不用这么复杂。python、matlab和opencv都有相应的函数，直接调用函数就可以返回我们的结果。

在python中，可以使用skimage这个图像处理库来进行转换：

skimage.color.rgb2lab(rgb)

在matlab中，相应的函数为：

I = rgb2lab(image)

得到的颜色空间是在Lab颜色空间的规定范围内(L: [0, 100], a: [-128, 127], b: [-128, 127]

在opencv中，相应的函数为：

cvCvtColor(image, lab_image, CV_BGR2LAB) 

其中lab_image三通道L，a，b的值都是大于100的值，并不是在规定范围内(L: [0, 100], a: [-128, 127], b: [-128, 127]) 

具体两者转化之后的区别，本人认为前者应该是最为标准的，而后者是经过映射之后的结果，也就是将得到结果的负数部分映射到正数区间内，这样在显示的时候就可以直接显示了。

经过颜色空间转化之后，便得到了L、a、b三部分的信息，分别表示光照明暗、颜色信息a、颜色信息b。

这里上个图片看下效果：

  L     a  b

二、最小二乘加权滤波

这个滤波方式与双边滤波、引导滤波等都是图像保边滤波的经典。其原理都是通过在图像相对较为平坦的区域（低频信息）进行强滤波，而在图像的边角、目标边缘（高频信息）部分进行弱滤波，这样便可以在平滑图像的同时保持图像边缘部分受损失最小，从而保留图像的更多细节信息。

这部分内容可以参考（链接）。其matlab代码如下：

function OUT = wlsFilter(IN, lambda, alpha, L)
%WLSFILTER Edge-preserving smoothing based on the weighted least squares(WLS) 
%   optimization framework, as described in Farbman, Fattal, Lischinski, and
%   Szeliski, "Edge-Preserving Decompositions for Multi-Scale Tone and Detail
%   Manipulation", ACM Transactions on Graphics, 27(3), August 2008.
%
%   Given an input image IN, we seek a new image OUT, which, on the one hand,
%   is as close as possible to IN, and, at the same time, is as smooth as
%   possible everywhere, except across significant gradients in L.
%
% 最小二乘加权滤波器
%   Input arguments:
%   ----------------
%     IN              Input image (2-D, double, N-by-M matrix). 
%       
%     lambda          Balances between the data term and the smoothness
%                     term. Increasing lambda will produce smoother images.
%                     Default value is 1.0
%       
%     alpha           Gives a degree of control over the affinities by non-
%                     lineary scaling the gradients. Increasing alpha will
%                     result in sharper preserved edges. Default value: 1.2
%       
%     L               Source image for the affinity matrix. Same dimensions
%                     as the input image IN. Default: log(IN)
% 
%
%   Example 
%   -------
%     RGB = imread('peppers.png'); 
%     I = double(rgb2gray(RGB));
%     I = I./max(I(:));
%     res = wlsFilter(I, 0.5);
%     figure, imshow(I), figure, imshow(res)
%     res = wlsFilter(I, 2, 2);
%     figure, imshow(res)

if(~exist('L', 'var'))
    L = log(IN+eps);
end

if(~exist('alpha', 'var'))
    alpha = 1.2;
end

if(~exist('lambda', 'var'))
    lambda = 1;
end

smallNum = 0.0001;

[r,c] = size(IN);
k = r*c;

% Compute affinities between adjacent pixels based on gradients of L
dy = diff(L, 1, 1); %对L矩阵的第一维度上做差分，也就是下面的行减去上面的行，得到(N-1)xM维的矩阵
dy = -lambda./(abs(dy).^alpha + smallNum);
dy = padarray(dy, [1 0], 'post');%在最后一行的后面补上一行0
dy = dy(:);%按列生成向量，就是Ay对角线上的元素构成的矩阵

dx = diff(L, 1, 2); %对L矩阵的第二维度做差分，也就是右边的列减去左边的列，得到Nx(M-1)的矩阵
dx = -lambda./(abs(dx).^alpha + smallNum);
dx = padarray(dx, [0 1], 'post');%在最后一列的后面添加一列0
dx = dx(:);%按列生成向量，对应上面Ay的对角线元素


% Construct a five-point spatially inhomogeneous Laplacian matrix
B(:,1) = dx;
B(:,2) = dy;
d = [-r,-1];
A = spdiags(B,d,k,k);
%把dx放在-r对应的对角线上，把dy放在-1对应的对角线上

e = dx;
w = padarray(dx, r, 'pre'); w = w(1:end-r);
s = dy;
n = padarray(dy, 1, 'pre'); n = n(1:end-1);

D = 1-(e+w+s+n);
A = A + A' + spdiags(D, 0, k, k);%A只有五个对角线上有非0元素

% Solve
OUT = A\IN(:);%
OUT = reshape(OUT, r, c);

使用时，可以对该函数进行调用，代码如下：

f = imread(image);    %注意，这里的image为上一步得到Lab空间中的结果 L_
f = double(f);
I = f./max(f(:));
smooth = wlsFilter(I, 0.5);  %平滑，后面参数可以自行选取
detail = I - smooth；#细节

通过以上滤波过程，便得到了L空间中的平滑度信息与细节信息，综合以上信息，算法便获得了原始图像的平滑度信息smooth，细节信息detail， 颜色信息a， 颜色信息b，当然也还有原始RGB图像。

这里上个图片看下效果

          smooth                  detail

三、网络结构

前面所做的铺垫都是为了给神经网络进行特征提取，然后进行回归。

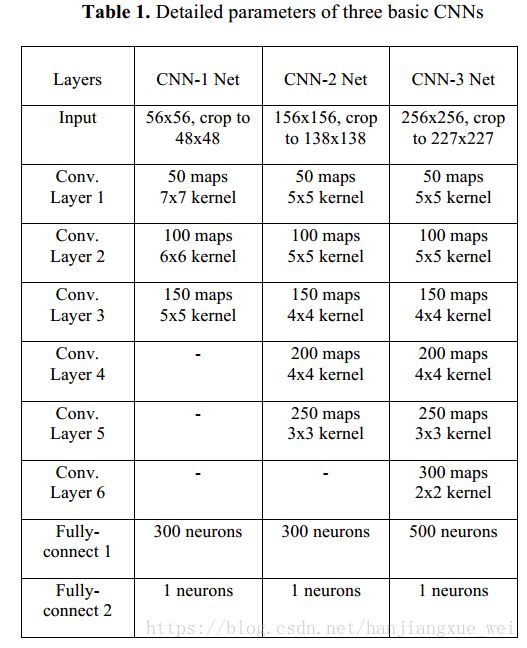
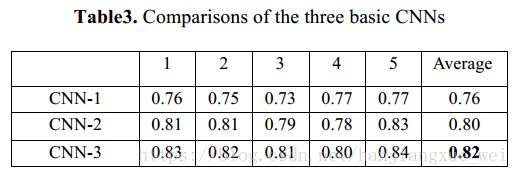
这里作者使用了三种类型的网络，并且进行了对比，结果如下：

其中，上图中的1-5表示作者进行了5-fold的交叉验证。最终结果为交叉验证结果的均值。当然，结果也表明，深层的网络有更强的特征提取能力，预测准确度也比浅层网络更高。

四、训练步骤

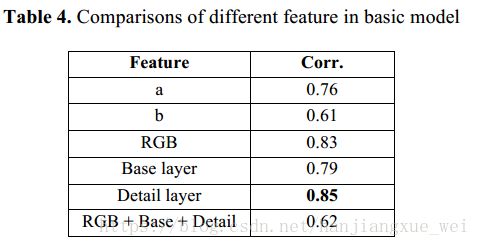
1、将得到的细节信息detail 首先喂给网络进行训练，训练达到一定的次数之后，再将平滑度信息smooth喂给网络，进行微调；最终将原始RGB图像再喂给网络，进行进一步微调。作者通过实验验证了这种方式的效果最好。对比如下：

注意， 在Table4 中，Base layer指的的图像的平滑度图像，也就是我们代码中的smooth。作者分别利用得到的不同信息进行了训练，之后发现用细节层训练结果的预测准确率最高，反而在用原始RGB图像进行预训练，用平滑度图像和细节层图像进行微调后，效果比较低，具体原因作者也并不是十分明白。总而言之，作者便决定使用了细节层进行网络的预训练。

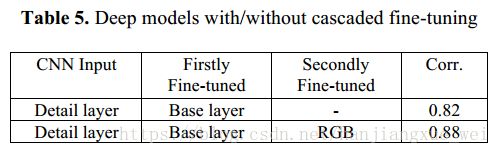
在Table5中，我们可以看到，经过细节层的预训练之后，利用smooth图像与RGB图像进行微调之后的结果，能够达到88%的相关度，效果提升非常明显。但具体为什么会这样，目前作者也不是特别清楚。

---------------------------------------------------------------------------------------------------------

文章也介绍完了，不过本人发现，作者在经过颜色空间转换之后，其实只用到了 L 亮度信息，并没有颜色信息加入（只是利用a、b信息进行了对比），而是在后面进行微调的时候，用到了RGB颜色信息。这有点让我不太理解。难道说，对于人脸图像来说，只利用其亮度信息就能够达到82%的效果，那人脸本身的颜色、光照、纹理等因素对人脸的影响就比较小？还是出于偶然，对于SCUT-FBP数据集，恰好明暗信息就能够表达出这样的结果？