整数规划
2.1秘籍内容
在上节课的学习过后,相信各位练武之人对于“数学规划”这一武功有个初步的了解,并且学习了该武功的第一式——线性规划,但对于某些生产进度问题、旅行推销员问题、工厂 选址问题、背包问题及分配问题等线性规划并不能高效的解决并且往往最优解难以满足条件,这时候我们便需要另一个招式——整数规划。那么何为整数规划呢?它和线性规划又有着怎样的区别和联系呢?下面我们来进一步了解一下。
 规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中, 变量限制为整数,则称为整数线性规划。如不加特殊说明,一般指整数线性规划。对于整数线性规划模型大致可分为两类:
规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中, 变量限制为整数,则称为整数线性规划。如不加特殊说明,一般指整数线性规划。对于整数线性规划模型大致可分为两类:
(i)变量全部限制为整数时,称纯(完全)整数规划。
(ii)变量部分限制为整数的,称混合整数规划。
整数规划这一招式,可谓是衍生于线性规划,但是又有其独特奥妙之处比如:
(i) 原线性规划有最优解,当自变量限制为整数后,其整数规划解出现下述情况:
①原线性规划最优解全是整数,则整数规划最优解与线性规划最优解一致。
②整数规划无可行解。
例 1 原线性规划为
min z= x 1 x_1 x1+ x 2 x_2 x2
2 x 1 x_1 x1+4 x 2 x_2 x2=5, x 1 ≥ 0 x1 \geq 0 x1≥0, x 2 ≥ 0 x2 \geq 0 x2≥0
其最优实数解为: x 1 x_1 x1=0, x 2 x_2 x2= 3 2 \frac{3}{2} 23,min z= 3 2 \frac{3}{2} 23.
若限制整数得: x 1 x_1 x1=0, x 2 x_2 x2=1,min z=2.
(ii) 整数规划最优解不能按照实数最优解简单取整而获得。也就是说关于整数规划最优解的求法应另有其他方式。
听完上面的讲述,大家是不是有一些头绪了,整数规划的基础实则为线性规划,合理运用上一招式中的修炼三大法,以及我们即将学习的几种修炼方法,相信整数规划问题定能迎刃而解。

2.2招式解析
2.2.1 (分枝定界法)
该方法首先是在上个世纪六十年代初由Land Doig 和 Dakin 等“武林高手”提出的。主要思路为,把全部可行解空间反复地分割为越来越小的子集,称为分枝;并且对每个子集内的解集计算一个目标下界(对于小值问题),这称为定界。在每次分枝后,凡是界限超出已知可行解集目标值的那些子集不再进一步分枝,这样,许多子集可不予考虑,这称剪枝。
听完这些是不是觉得分枝定界法还挺玄妙,但只要我们掌握分枝、定界、剪枝与比较三步修炼大法,下面通过解决一个实际问题,看看这个方法是否行之有效呢。
例 3 求解下述整数规划
Max z=40 x 1 x_1 x1+90 x 2 x_2 x2

解: (i)先不考虑整数限制,即解相应的线性规划B,得最优解
x 1 x_1 x1=4.8092, x 2 x_2 x2=1.8168,z=355.8779
可见问题B的最优解不符合整数条件。这时 z 是问题 A的优目标函数值 z* 的上界,记作 z ⃗ \vec z z。而 x 1 x_1 x1=0, x 2 x_2 x2=0,显然是问题 A的一个整数可行解,这时z=0,是z* 的一个下界,记作 z ‾ \underline{z} z, 0 ≤ 0 \leq 0≤ z* ≤ 356 \leq 356 ≤356 。
(ii)因为 x 1 x_1 x1与 x 2 x_2 x2当前均为非整数,故不满足整数要求,任选一个进行分枝。设选进行分枝,把可行集分成 2 个子集:
x 1 x_1 x1 ≤ \leq ≤[4.8092]=4, x 2 x_2 x2 ≥ \geq ≥[4.8092]+1=5
因为 4 与 5 之间无整数,故这两个子集的整数解必与原可行集合整数解一致。这 一步称为分枝。这两个子集的规划及求解如下:
问题 B 1 B_1 B1:Max z=40 x 1 x_1 x1+90 x 2 x_2 x2
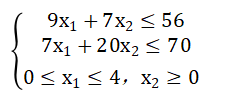
最优解为: x 1 x_1 x1=4.0, x 2 x_2 x2=2.1,z=349.
问题 B 2 B_2 B2:Max z=40 x 1 x_1 x1+90 x 2 x_2 x2
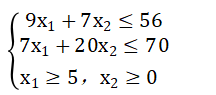
最优解为: x 1 x_1 x1=5.0, x 2 x_2 x2=1.57,z=341.4.
再定界:0 ≤ \leq ≤ z* ≤ \leq ≤ 349.
(iii)对问题 再进行分枝得问题B11和B12,它们的最优解为:
B11: x 1 x_1 x1=4.0, x 2 x_2 x2=2.0,z11=340.
B12: x 1 x_1 x1=1.43, x 2 x_2 x2=3.0,z12=327.14.
再定界:340 ≤ \leq ≤ z* ≤ \leq ≤ 341,并将B12剪枝。
(iv)对问题B2再进行分枝得问题B21和B22,它们的最优解为
B21: x 1 x_1 x1=5.44, x 2 x_2 x2=1.0,z21=308.
B22:无可行解。
将B21,B22剪枝。
于是可以断定原问题的最优解为:
x 1 x_1 x1=4.0, x 2 x_2 x2=2.0,z*=340.
从以上解题过程可得用分枝定界法求解纯整数规划和混合整数规划问题的步骤:
1.首先忽略整数约束求解,求得原问题的最优解X
2.如果决策变量x;本是整数要求,但是得到的结果X; =u (不是整数),则将原问题归结为2个区域的线性规划求解,这个两个区域为分别增加约束条件
x i x_i xi ≤ \leq ≤ceil(u) 和 x i x_i xi ≤ \leq ≤floor(u)
3.然后分别都这两个规划模型重复上面的步骤,直到满足整数要求为止。
4.再选出最优解。
大家现在对于分枝定界法求解整数规划问题应该有了一定的了解,除此之外我们还有几种很实用的招式供大家学习了解。我们一起看看吧。

2.2.2 0-1型整数规划
所谓0-1型整数规划就是变量的取值只能是0或者1,这样的话,其实我们可以将不同的整数规划转化成0-1规划。下面我们来看一个实际问题 这里我们就可以直接列出一个是0-1规划的方程,设的变量 x i x_i xi,“1”表示被选中,“0”表示没被选中。0-1型整数规划的特点就是相互排斥的约束条件可以转化成同类型的。比如:
这里我们就可以直接列出一个是0-1规划的方程,设的变量 x i x_i xi,“1”表示被选中,“0”表示没被选中。0-1型整数规划的特点就是相互排斥的约束条件可以转化成同类型的。比如:

2.2.3其他三种方法
(1)穷举法,是一种很有效的方法,而且在某些情况下只能穷举。
(2)过渡隐枚举法
1.先试探性求一个可行解X(随便带入求值)
2.然后根据是求极大值还是极小值,如果是求极大值,那么凡是目标值
3.改进新的过滤条件
4.然后验证目标值,最终求得。
(3)蒙特卡洛法(随机抽样法)
就是选择不穷举全部点,而是采用随机的方式来抽取样本估计整体,如果样本足够大,可信度是很大的。

2.3武器栏
只见蓝光一闪,MATLAB之剑横空出世,正所谓招配剑,方能招招命中。
解非线性整数规划-----------蒙特卡罗方法
![]()
![]()
![]()
![]()
![]()
![]()
Matlab实现整数规划求解(分枝定界法):
function r=checkint(x)
%判断x(i)是不是整数了。是的话r(i)返回1,不是的话,返回0
%输入参数:x X向量
%输出参数:r R向量
for i=1:length(x)
if(min(abs(x(i)-floor(x(i))),abs(x(i)-ceil(x(i))))<1e-3)
r(i)=1;
else
r(i)=0;
end
Function val=isrowinmat(arow,mat)
%用来判断mat中是否包含与arow一样的向量
%输入变量:arow 向量
% mat 矩阵
%输出变量:val 1表示有,0表示没有
val=0;
rows=size(mat,1);
for i=1:rows
temp=(mat(i,:)==arow);
if length(find(temp==0))==0
val=1;
return;
else
val=0;
end;
end
function [x,fval,exitflag,output,lambda]=linprogdis(ifint,f,A,b,Aeq,beq,lb,ub,x0,options)
% 用法
% [x,fval,exitflag,output,lambda]=lpint(ifint.f,A,b,Aeq,beq)
% [x,fval,exitflag,output,lambda]=lpint(ifint,f,A,b,Aeq,beq,lb)
% [x,fval,exitflag,output,lambda]=lpint(ifint,f,A,b,Aeq,beq,lb,ub)
% [x,fval,exitflag,output,lambda]=lpint(ifint,f,A,b,Aeq,beq,lb,ub,x0)
% [x,fval,exitflag,output,lambda]=lpint(ifint,f,A,b,Aeq,beq,lb,ub,x0,options)
if nargin<10, options=[]; end
if nargin<9, x0=[]; end
if nargin<8, ub=inf*ones(size(f)); end
if nargin<7, lb=zeros(size(f)); end
[x,fval,exitflag,output,lambda]=linprog(f,A,b,Aeq,beq,lb,ub,x0,options);
if exitflag<=0 %表示线性规划没有最优解
return
end
v1=find(ifint==1); %找到需要整数规划的变量的下标
temp=x(v1);%如果不是要求整数规划的就可以返回了。
if isempty(temp)
return
end
v2=find(checkint(temp)==0);
if isempty(v2) %都是整数,得到最众解
return
end
k=v1(v2(1));
temp1=zeros(1,length(f));
temp1(k)=1;
low=floor(x(k));
if isrowinmat([temp1,low],[A,b])==1
thisA=A;
thisb=b;
else
thisA=[A;temp1];
thisb=b;
thisb(end+1)=low;
end
[x1,fval1,exitflag1,output1,lambda1]=linprogdis(ifint,f,thisA,thisb,Aeq,beq,lb,ub,x0,options);
temp2=zeros(1,length(f));
temp2(k)=-1;
high=-ceil(x(k));
if isrowinmat([temp2,high],[A,b])==1
thisA=A;
thisb=b;
else
thisA=[A;temp2];
thisb=b;
thisb(end+1)=high;
end
[x2,fval2,exitflag2,output2,lambda2]=linprogdis(ifint,f,thisA,thisb,Aeq,beq,lb,ub,x0,options);
if (isempty(v2) && ((exitflag1>0 && exitflag2<=0 && fval<=fval)||(exitflag2>0 && exitflag1<=0 && fval<=fval2)||(exitflag1>0 && exitflag2>0 && fval<=fval1 && fval<=fval2)))
disp('error call');
return ; %表示都是整数
end
if exitflag1>0&&exitflag2<=0
x=x1;
fval=fval1;
exitflag=exitflag1;
output=output1;
lambda=lambda1;
elseif exitflag1<=0&&exitflag2>0
x=x2;
fval=fval2;
exitflag=exitflag2;
output=output2;
lambda=lambda2;
elseif exitflag1>0 && exitflag2>0
if fval1