keras lastm循环神经网络训练验证测试
在keras 上实践,通过keras例子来理解lastm循环神经网络
本文是对这篇博文的翻译和实践:
http://machinelearningmastery.com/understanding-stateful-lstm-recurrent-neural-networks-python-keras/
阅读本文章以后,你将要知道:
一)怎么在keras上实习一个普通的lstm循环神经网络。
二)在lstm中怎样小心的利用好时间状态特征
三)怎样在lstm上实现状态的预测。
本文在一个很简单的例子上说明lstm的使用和lstm的特点,通过对这个简化例子的理解,可以帮助我们对一般的序列预测问题和序列预测问题有更高的理解和使用。
先导入我们会用到的包。
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils- 1
- 2
- 3
- 4
- 5
然后我们把我们的数据集–一个字母表转化为keras可以处理的形式。
# define the raw dataset
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
# create mapping of characters to integers (0-25) and the reverse
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))- 1
- 2
- 3
- 4
- 5
ok,现在我们在来制造我的input和output
数据集。
我们先创造这样一个数据集,用一个字母,来预测下一个字母是什么。
# prepare the dataset of input to output pairs encoded as integers
seq_length = 1
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print seq_in, '->', seq_out- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
我们运行上面的代码,来观察现在我们的input和output数据集是这样一种情况
:
A -> B
B -> C
C -> D
D -> E
E -> F
F -> G
G -> H
H -> I
I -> J
J -> K
K -> L
L -> M
M -> N
N -> O
O -> P
P -> Q
Q -> R
R -> S
S -> T
T -> U
U -> V
V -> W
W -> X
X -> Y
Y -> Z- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
input是一个一个字母的序列,output是一个一个的序列。
ok,就在这样的数据集上来应用我们的lstm。看看会有什么结果?
这时候dataX是一个一个用字母组成的序列,
但是还要转换一下格式,才能用到keras上。
# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))- 1
- 2
然后我们需要把我们的整数值归一化到0~1的区间上。
# normalize
X = X / float(len(alphabet))- 1
- 2
最后,我们可以把这个问题当作是一个序列的分类问题,26个不同的字母代表了不同的类别,我们用keras的内置的 to_categorical()函数把datay进行 one——hot编码,作为输出层的结果。
一个字母——一个字母映射!
我们通过lstm在这个问题上的预测,会发现这对lstm循环网络来说是很难解决的问题。
keras上lstm用于上述问题的代码如下:
# create and fit the model
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, nb_epoch=500, batch_size=1, verbose=2)- 1
- 2
- 3
- 4
- 5
- 6
对与这个小问题,我用了掉炸天的Adam
算法,经历了500次的迭代,最后我们得到了: 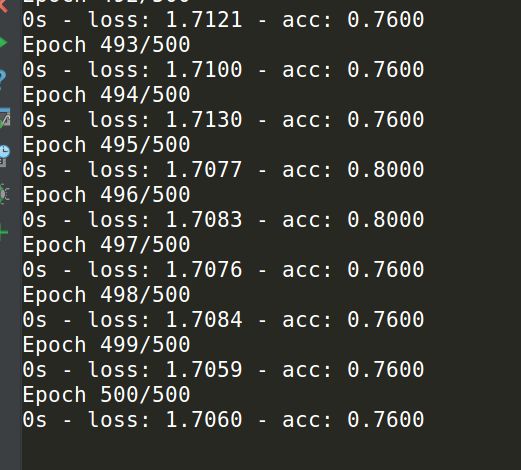
这样的结果,真是日了狗了。
我们可以看到这样的问题对lstm循环神经网络来说真的难以处理。
原因是可怜的lstm单元根本没有可以利用的上下文章信息。
这是对lstm的愚弄,把它当成了普通的多层感知机来对待。
Three-Char Feature Window to One-Char Mapping
这个标题不知道怎么翻译。。
我们把输入从一个字符升到三个字符。
# prepare the dataset of input to output pairs encoded as integers
seq_length = 3- 1
- 2
就像这样:
ABC -> D
BCD -> E
CDE -> F- 1
- 2
- 3
全部的代码如下:
# Naive LSTM to learn three-char window to one-char mapping
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils
# fix random seed for reproducibility
numpy.random.seed(7)
# define the raw dataset
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
# create mapping of characters to integers (0-25) and the reverse
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
# prepare the dataset of input to output pairs encoded as integers
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print seq_in, '->', seq_out
# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), 1, seq_length))
# normalize
X = X / float(len(alphabet))
# one hot encode the output variable
y = np_utils.to_categorical(dataY)
# create and fit the model
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, nb_epoch=500, batch_size=1, verbose=2)
# summarize performance of the model
scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))
# demonstrate some model predictions
for pattern in dataX:
x = numpy.reshape(pattern, (1, 1, len(pattern)))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0)
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print seq_in, "->", result- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
运行结果如下:
Model Accuracy: 86.96%
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> M
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> P
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> S
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> U
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> Y
['U', 'V', 'W'] -> Z
['V', 'W', 'X'] -> Z
['W', 'X', 'Y'] -> Z- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
通过,结果我们发现有了一点点的提升,但是这一点点的提升未必是真实的,梯度下降算法本来就是具有随机性的。
也就是说我们再一次的错误使用了lstm循环神经网络。
我们确实给了上下文,但是并不是合适的方式,
我们把ABC当成了一个特征,而不是在一个时间端上的三个独立的特征。 Indeed, the sequences of letters are time steps of one feature rather than one time step of separate features. (原文是这么说的,我翻译不好。。。)
keras实践循环的正确打开方式!
在keras中,利用lstm的关键是以时间序列的方法来提供上下文,而不是像其他网络结构一样,通过windowed features的方式。
这次我们还是采用这样的训练方式,
ABC -> D
BCD -> E
CDE -> F
DEF -> G- 1
- 2
- 3
- 4
我们这次唯一改变的地方是下面这里:
# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))- 1
- 2
timesteps这个参数,我们设置了3
,而不是前面的1。
也就是说我们把ABC 看成独立的三个特征 A B
C组成的时间序列,而不是把ABC看成一个总的特征。
这就是keras中lastm循环神经网络的正确打开的方式。
我的理解是,
这样在训练 ABC——D的时候,BCD,CDE,都可以发挥作用。而最开始那种使用方法,
只是利用了ABC——D这样一个训练样本。
完整代码如下:
# Naive LSTM to learn three-char time steps to one-char mapping
import numpy
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.utils import np_utils
# fix random seed for reproducibility
numpy.random.seed(7)
# define the raw dataset
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
# create mapping of characters to integers (0-25) and the reverse
char_to_int = dict((c, i) for i, c in enumerate(alphabet))
int_to_char = dict((i, c) for i, c in enumerate(alphabet))
# prepare the dataset of input to output pairs encoded as integers
seq_length = 3
dataX = []
dataY = []
for i in range(0, len(alphabet) - seq_length, 1):
seq_in = alphabet[i:i + seq_length]
seq_out = alphabet[i + seq_length]
dataX.append([char_to_int[char] for char in seq_in])
dataY.append(char_to_int[seq_out])
print seq_in, '->', seq_out
# reshape X to be [samples, time steps, features]
X = numpy.reshape(dataX, (len(dataX), seq_length, 1))
# normalize
X = X / float(len(alphabet))
# one hot encode the output variable
y = np_utils.to_categorical(dataY)
# create and fit the model
model = Sequential()
model.add(LSTM(32, input_shape=(X.shape[1], X.shape[2])))
model.add(Dense(y.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, nb_epoch=500, batch_size=1, verbose=2)
# summarize performance of the model
scores = model.evaluate(X, y, verbose=0)
print("Model Accuracy: %.2f%%" % (scores[1]*100))
# demonstrate some model predictions
for pattern in dataX:
x = numpy.reshape(pattern, (1, len(pattern), 1))
x = x / float(len(alphabet))
prediction = model.predict(x, verbose=0)
index = numpy.argmax(prediction)
result = int_to_char[index]
seq_in = [int_to_char[value] for value in pattern]
print seq_in, "->", result- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
最终的训练结果是
Model Accuracy: 100.00%
['A', 'B', 'C'] -> D
['B', 'C', 'D'] -> E
['C', 'D', 'E'] -> F
['D', 'E', 'F'] -> G
['E', 'F', 'G'] -> H
['F', 'G', 'H'] -> I
['G', 'H', 'I'] -> J
['H', 'I', 'J'] -> K
['I', 'J', 'K'] -> L
['J', 'K', 'L'] -> M
['K', 'L', 'M'] -> N
['L', 'M', 'N'] -> O
['M', 'N', 'O'] -> P
['N', 'O', 'P'] -> Q
['O', 'P', 'Q'] -> R
['P', 'Q', 'R'] -> S
['Q', 'R', 'S'] -> T
['R', 'S', 'T'] -> U
['S', 'T', 'U'] -> V
['T', 'U', 'V'] -> W
['U', 'V', 'W'] -> X
['V', 'W', 'X'] -> Y
['W', 'X', 'Y'] -> Z- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
66666!吊的不行!但是我们还没有展示出循环神经网络的强大之,因为上面这个问题我们用多层感知器,足够多的神经元,足够多的迭代次数也可以很好的解决。(三层神经网络拟合任意可以表示的函数)
那么接下来就是展示循环神经网络的独到之处!!
LSTM State Within A Batch
keras实现的lstm在每一个batch以后,都重置了lstm的状态。