利用运动学实现导弹仿真飞行

利用Unity实现导弹飞行的算法网上案例很多，本篇博客主要给读者介绍如何将所学算法运用到项目开发的实战教程。
我们将使用运动学原理实现仿真，这意味着我们将只在计算中使用速度，而不考虑物体上的质量和其他作用的物理力，这些力会影响物体的运动，比如阻力。为了能够模拟导弹击中目标，我们将考虑以下变量:
发射速度，发射角度，导弹距离目标的距离。
很多程序员学过算法，学过数据结构，但是在项目开发过程中就不会灵活运用了，所以有些人觉得以前学的知识没用，其实这是完全错误的，大学读书的过程也是一种培养能力的过程，大学所学的都是一些基础知识，他也是为我们以后能够自学打下基础。而且大学学习的算法在游戏开发中用的非常多，我们也借助本篇博客告诉读者如何将所学知识应用到项目开发中。
下面我们就围绕算法讲解实现过程：
我们将从运动的运动学方程开始，其实也就是我们说的抛物线方程，它描述了基于初始速度和加速度所获取到的位置:

P1是最后的位置，P0是初始位置，v0初始速度，a加速度，t是运动持续时间。我们在纸上推导一下数学公式，看能到什么结果？

a是发射角度，V0是初始速度，V0x，V0y是初始速度V0的两个分量，H是沿着y轴位置距离差，R是沿x轴的位置距离差，t就是抛物线运动的时间。
通过我们的推演可以知道以下几个条件：一是，在x轴的运动距离是R，初始速度是V0x，运行时间是t；二是，在y轴运动距离是H，初始速度是V0y，重力G以及运行轨迹的时间t；三是，沿着y轴的距离H, x轴R, G重力，发射角α和初速度V0x也就是V0的分量。利用我们的这些已经计算好的公式，最终推导出上图的公式如下所示：

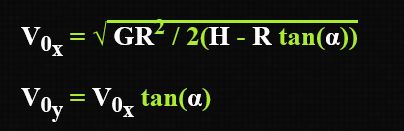
在解答方程之前，我们还要解决一个问题就是导弹朝向目标问题，在Unity中提供了LookAt函数，再思考目标物体和导弹的高度不同的情况，虽然我们希望在下面的gif中使用左边的效果，但是如果使用LookAt()函数，我们将获得右边的效果。

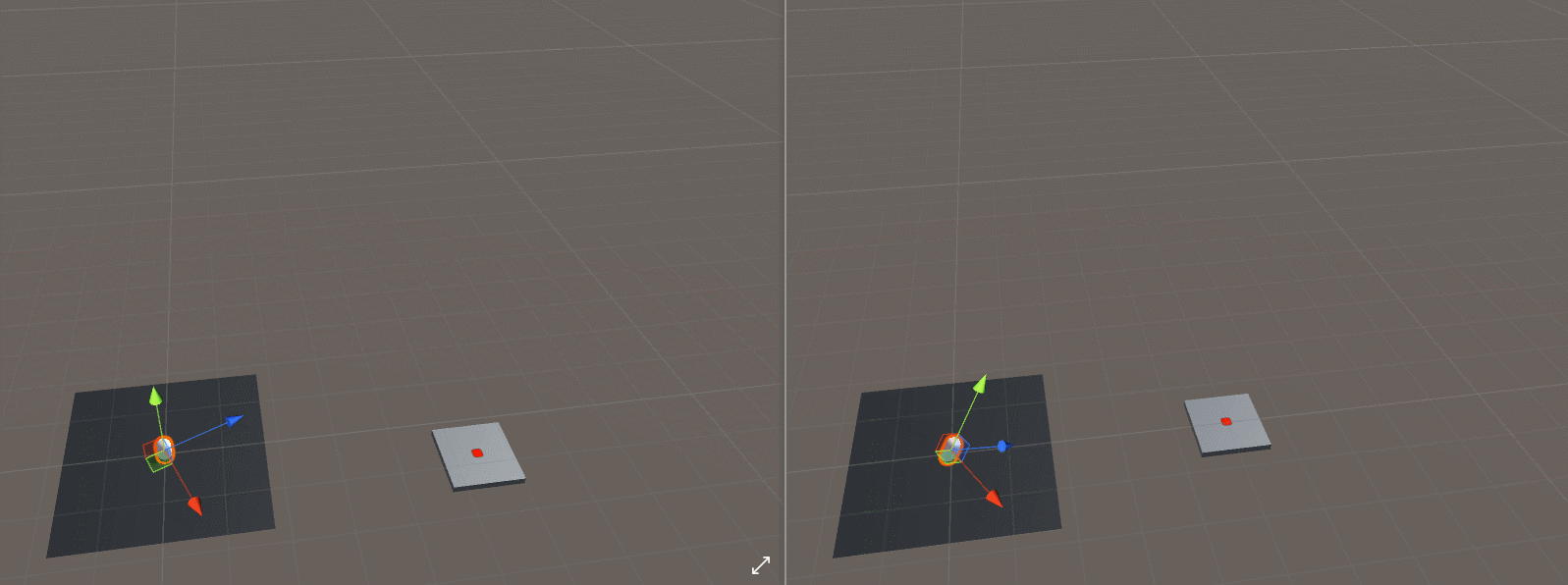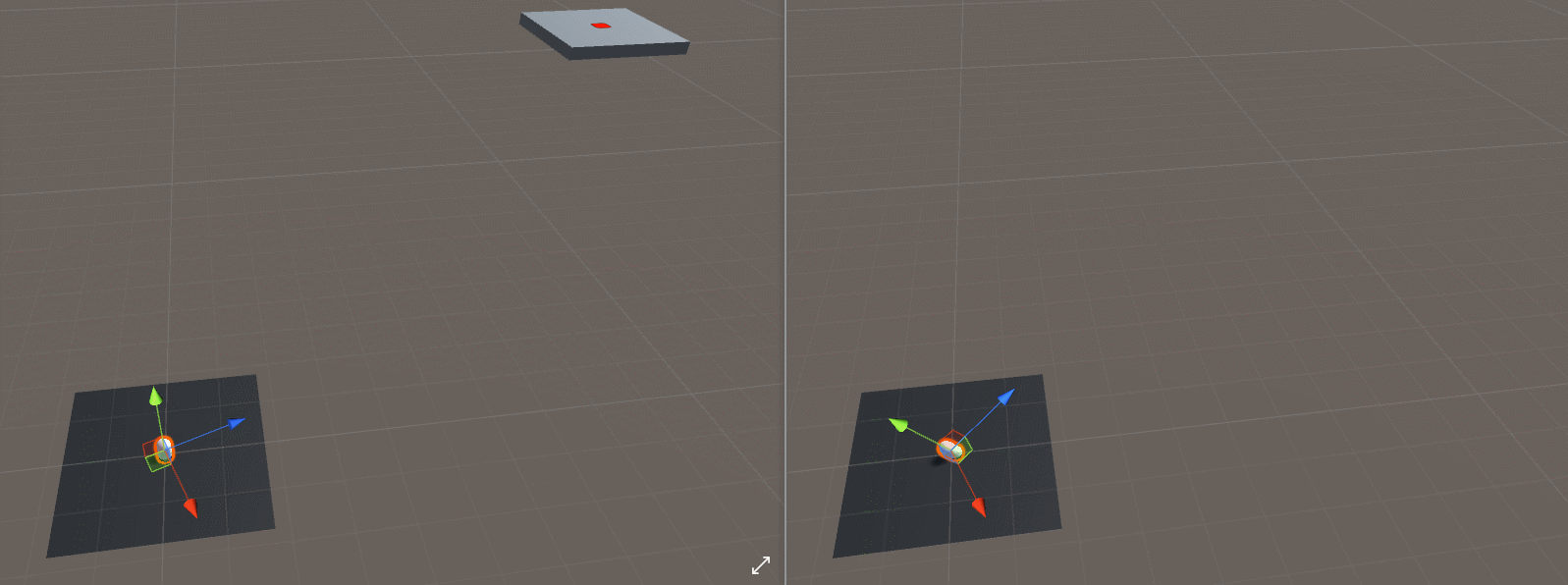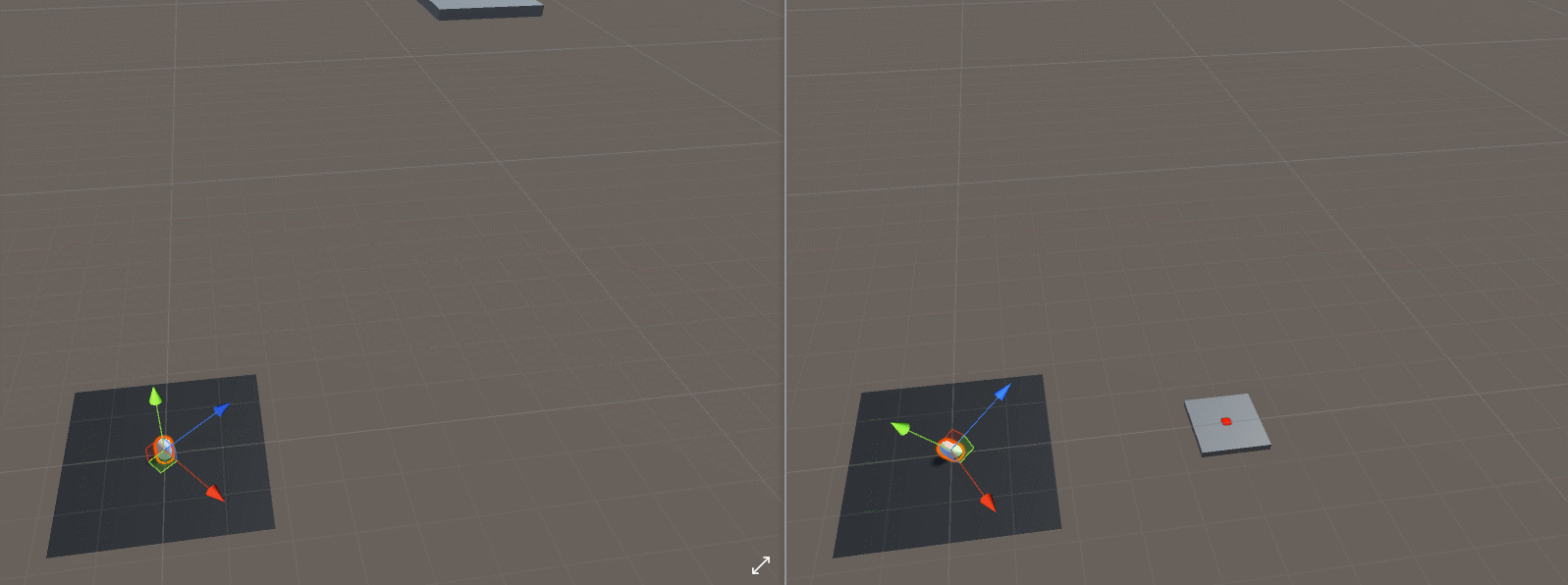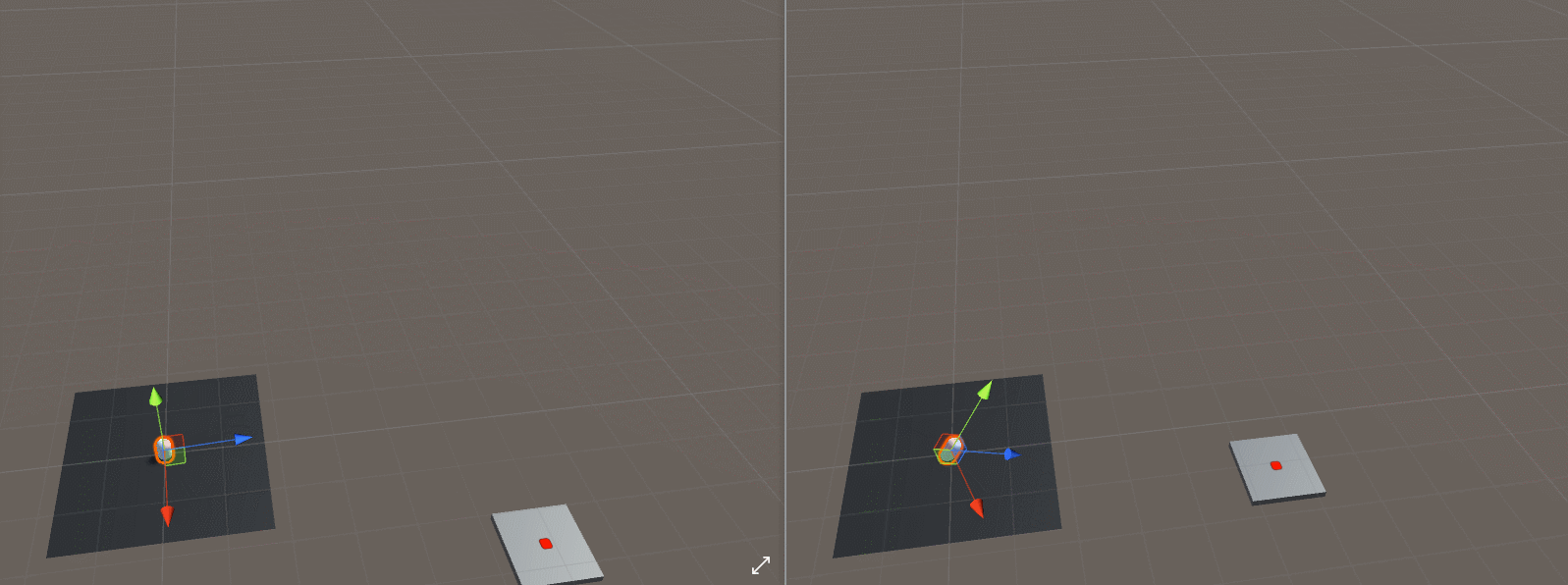
如果我们像这样放弃目标的Y分量和抛射体的位置，我们可以达到预期的“转向”效果，代码如下所示：

void Launch()
{
    // think of it as top-down view of vectors: 
    //   we don't care about the y-component(height) of the initial and target position.
    Vector3 projectileXZPos = new Vector3(transform.position.x, 0.0f, transform.position.z);
    Vector3 targetXZPos = new Vector3(TargetObjectTF.position.x, 0.0f, TargetObjectTF.position.z);
    
    // rotate the object to face the target
    transform.LookAt(targetXZPos);
    
    // ...
}

接下来我们开始解方程，解方程首先要确定上述公式中每个变量所能标识的含义，先看G，在Unity中，它表示的是重力的y值，G=Physics.gravity.y;
tan(α)=Mathf.Tan(LaunchAngle * Mathf.Deg2Rad);
R = Vector3.Distance(projectileXZPos, targetXZPos);
H=TargetObjectTF.position.y - transform.position.y;
在Unity中的表示如下所示：
公式计算出来后，我们要将公式用编程语言表达出来，这个也就是所谓的理论联系实际，对应代码如下所示：

void Launch()
{
    // ...

    // shorthands for the formula
    float R = Vector3.Distance(projectileXZPos, targetXZPos);
    float G = Physics.gravity.y;
    float tanAlpha = Mathf.Tan(LaunchAngle * Mathf.Deg2Rad);
    float H = (TargetObjectTF.position.y + GetPlatformOffset()) - transform.position.y;
    
    // calculate initial speed required to land the projectile on the target object 
    float Vz = Mathf.Sqrt(G * R * R / (2.0f * (H - R * tanAlpha)) );
    float Vy = tanAlpha * Vz;

    // create the velocity vector in local space and get it in global space
    Vector3 localVelocity = new Vector3(0f, Vy, Vz);

    // ...
}

以上我们的计算数值是在局部空间中计算得到的，我们的导弹发射是在世界空间中，所以还需要一个矩阵转换，Unity已经为我们想到了，使用函数：Transform.TransformDirection()
这样我们的导弹飞行函数就完善了，完整的导弹发射函数如下所示：

void Launch()
{
    // think of it as top-down view of vectors: 
    //   we don't care about the y-component(height) of the initial and target position.
    Vector3 projectileXZPos = new Vector3(transform.position.x, 0.0f, transform.position.z);
    Vector3 targetXZPos = new Vector3(TargetObjectTF.position.x, 0.0f, TargetObjectTF.position.z);
    
    // rotate the object to face the target
    transform.LookAt(targetXZPos);

    // shorthands for the formula
    float R = Vector3.Distance(projectileXZPos, targetXZPos);
    float G = Physics.gravity.y;
    float tanAlpha = Mathf.Tan(LaunchAngle * Mathf.Deg2Rad);
    float H = TargetObjectTF.position.y - transform.position.y;

    // calculate the local space components of the velocity 
    // required to land the projectile on the target object 
    float Vz = Mathf.Sqrt(G * R * R / (2.0f * (H - R * tanAlpha)) );
    float Vy = tanAlpha * Vz;

    // create the velocity vector in local space and get it in global space
    Vector3 localVelocity = new Vector3(0f, Vy, Vz);
    Vector3 globalVelocity = transform.TransformDirection(localVelocity);

    // launch the object by setting its initial velocity and flipping its state
    rigid.velocity = globalVelocity;
    bTargetReady = false;
}

上述代码，对应的实现效果如下所示：

这里还需要解决的问题就是导弹的飞行方向，我们的导弹不仅要命中目标还要方向时时朝向目标，就比如下图所示的：

关于朝向问题，使用Unity提供的函数lookat()改变导弹的方向，使其局部向前矢量对准目标方向，我们可以利用碰撞器组件来检测导弹是否触地，并根据速度矢量更新其旋转，从而解决这个问题。更新导弹旋转使用的函数是：Quaternion.LookRotation（），对应的代码实现如下所示：

public class Trajectory : MonoBehaviour
{
    //...

    // state
    private bool bTargetReady;
    private bool bTouchingGround;

    //...

    // Update is called once per frame
    void Update ()
    {
        // ...

        if (!bTouchingGround && !bTargetReady)
        {
            // update the rotation of the projectile during trajectory motion
            transform.rotation = Quaternion.LookRotation(rigid.velocity);
        }
    }

    void OnCollisionEnter()
    {
        bTouchingGround = true;
    }

    void OnCollisionExit()
    {
        bTouchingGround = false;
    }
}

对应的Unity实现如下所示：

显然上图并不是我们想要的结果，我们希望我们的正向向量指向圆柱体顶端的默认方向，如下面的全局空间向量所示:

四元数的一个优点是可以通过使用乘法运算符Quaternion.operator*()来组合它们。我们可以将从quaternion . lookrotation()函数中获得的旋转与初始旋转initialRotation 结合起来，从而为导弹对象实现正确的轨迹方向。我们把从右到左的旋转组合起来，如下所示:

transform.rotation = Quaternion.LookRotation(rigid.velocity) * initialRotation;

还要注意，组合旋转不是交换操作，所以乘法的顺序很重要(a B != B a)。我们实现“组合旋转”的方法和它的数学细节可以参考网址：
https://math.stackexchange.com/questions/331539/combining-rotation-quaternions/331548#331548
如下所示：

这意味着四元数.LookRotation(rigid.velocity) * initialRotation将首先对对象应用initialRotation来实现“我们想要的默认方向”，然后应用LookRotation(rigid.velocity)来沿弹道轨迹旋转导弹，导弹会指向速度方向，如下图所示。

demo下载地址：链接：https://pan.baidu.com/s/1-3R9HN045xVJlAejTjl7gQ
提取码：ct11

参考网址：
https://gamedev.stackexchange.com/questions/114759/how-do-i-set-angular-velocity-torque-so-that-its-pointing-to-velocity-direction
https://en.wikipedia.org/wiki/Projectile_motion
https://en.wikipedia.org/wiki/Trajectory
https://en.wikipedia.org/wiki/Kinematics
https://en.wikipedia.org/wiki/Trigonometry
https://en.wikipedia.org/wiki/Quaternion
https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
https://docs.unity3d.com/ScriptReference/Quaternion.html
https://docs.unity3d.com/Manual/QuaternionAndEulerRotationsInUnity.html