read data
library(quantmod) # 加载包
getSymbols('^HSI', from='1989-12-01',to='2013-11-30') # 从Yahoo网站下载恒生指数日价格数据
dim(HSI) # 数据规模
names(HSI) # 数据变量名称
chartSeries(HSI,theme='white') # 画出价格与交易的时序图
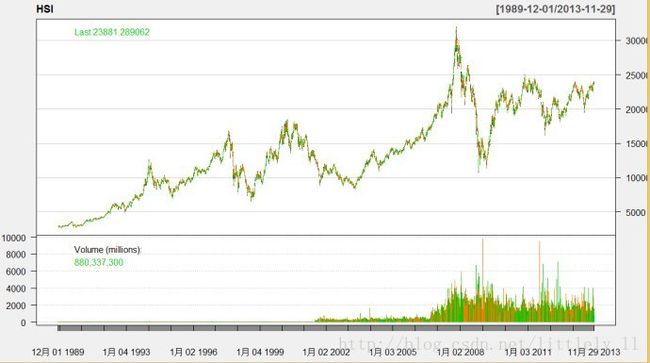
HSI <-read.table('HSI.txt') # 或者从硬盘中读取恒生指数日价格数据
HSI <-as.xts(HSI) # 将数据格式转化为xts格式
compute return series
ptd.HSI <-HSI$HSI.Adjusted # 提取日收盘价信息
rtd.HSI <-diff(log(ptd.HSI))*100 # 计算日对数收益
rtd.HSI <-rtd.HSI[-1,] # 删除一期缺失值
plot(rtd.HSI) # 画出日收益序列的时序图
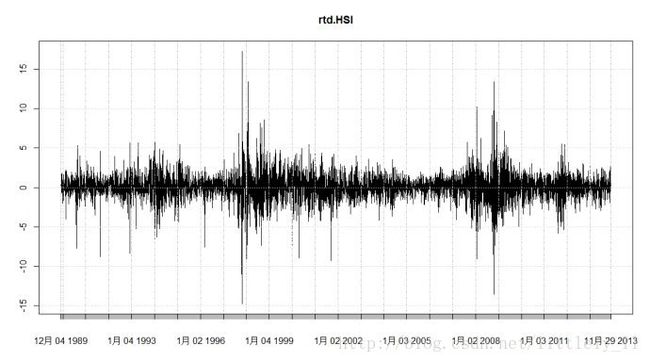

ptm.HSI <-to.monthly(HSI)$HSI.Adjusted # 提取月收盘价信息
rtm.HSI <-diff(log(ptm.HSI))*100 # 计算月对数收益
rtm.HSI <-rtm.HSI[-1,] # 删除一期缺失值
plot(rtm.HSI) # 画出月收益序列的时序图
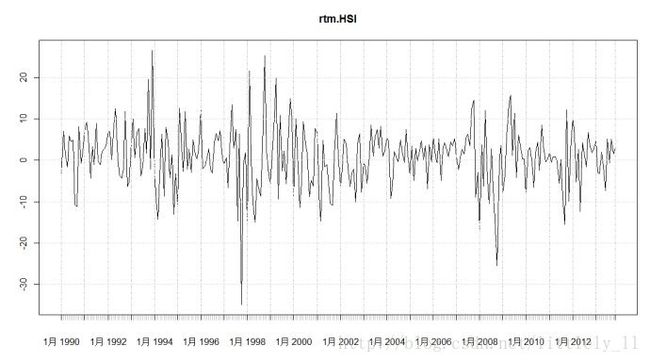
detach(package:quantmod)
ARCH效应检验
# rtm.HSI <- as.numeric(rtm.HSI)
ind.outsample <- sub(' ','',substr(index(rtm.HSI), 4, 8)) %in%'2013' #设置样本外下标:2013年为样本外
ind.insample <-!ind.outsample # 设置样本内下标:其余为样本内
rtm.insample <- rtm.HSI[ind.insample]
rtm.outsample <- rtm.HSI[ind.outsample]
Box.test(rtm.insample, lag=12,type='Ljung-Box') # 月收益序列不存在自相关
Box.test(rtm.insample^2, lag=12,type='Ljung-Box') # 平方月收益序列存在自相关
FinTS::ArchTest(x=rtm.insample,lags=12) # 存在显著的ARCH效应
模型定阶
epst <- rtm.insample -mean(rtm.insample) # 均值调整对数收益
par(mfrow=c(1,2))
acf(as.numeric(epst)^2, lag.max=20, main='平方序列')
pacf(as.numeric(epst)^2, lag.max=20,main='平方序列')
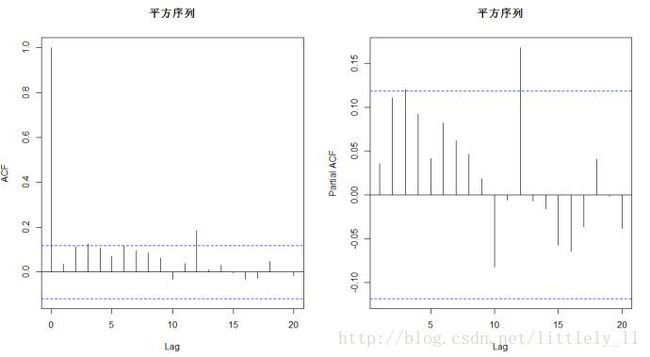
建立GARCH类模型
library(fGarch)
GARCH.model_1 <- garchFit(~garch(1,1), data=rtm.insample,trace=FALSE) # GARCH(1,1)-N模型
GARCH.model_2 <- garchFit(~garch(2,1), data=rtm.insample,trace=FALSE) # GARCH(1,2)-N模型
GARCH.model_3 <- garchFit(~garch(1,1), data=rtm.insample,cond.dist='std', trace=FALSE) #GARCH(1,1)-t模型
GARCH.model_4 <- garchFit(~garch(1,1), data=rtm.insample,cond.dist='sstd', trace=FALSE) #GARCH(1,1)-st模型
GARCH.model_5 <- garchFit(~garch(1,1), data=rtm.insample,cond.dist='ged', trace=FALSE) #GARCH(1,1)-GED模型
GARCH.model_6 <- garchFit(~garch(1,1), data=rtm.insample,cond.dist='sged', trace=FALSE) #GARCH(1,1)-SGED模型
summary(GARCH.model_1)
summary(GARCH.model_3)
plot(GARCH.model_1)
提取GARCH类模型信息
vol_1 <-fBasics::volatility(GARCH.model_1) # 提取GARCH(1,1)-N模型得到的波动率估计
sres_1 <- residuals(GARCH.model_1,standardize=TRUE) # 提取GARCH(1,1)-N模型得到的标准化残差
vol_1.ts <- ts(vol_1, frequency=12, start=c(1990, 1))
sres_1.ts <- ts(sres_1, frequency=12, start=c(1990, 1))
par(mfcol=c(2,1))
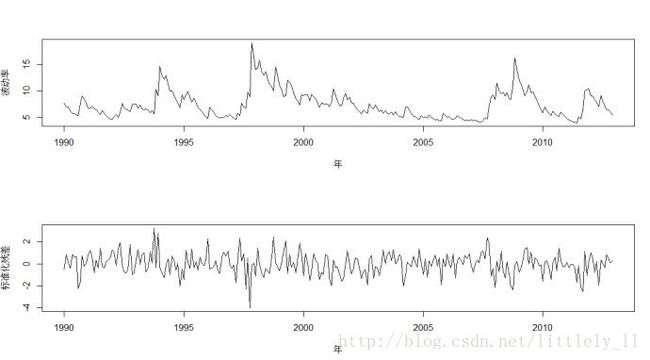
plot(vol_1.ts, xlab='年', ylab='波动率')
plot(sres_1.ts, xlab='年', ylab='标准化残差')
模型检验
par(mfrow=c(2,2))
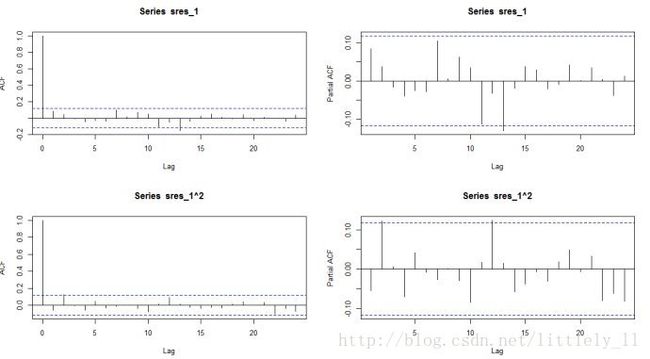
acf(sres_1, lag=24)
pacf(sres_1, lag=24)
acf(sres_1^2, lag=24)
pacf(sres_1^2, lag=24)

par(mfrow=c(1,1))
qqnorm(sres_1)
qqline(sres_1)
模型预测
pred.model_1 <- predict(GARCH.model_1, n.ahead = 11, trace =FALSE, mse = 'cond', plot=FALSE)
pred.model_2 <- predict(GARCH.model_2, n.ahead = 11, trace =FALSE, mse = 'cond', plot=FALSE)
pred.model_3 <- predict(GARCH.model_3, n.ahead = 11, trace =FALSE, mse = 'cond', plot=FALSE)
pred.model_4 <- predict(GARCH.model_4, n.ahead = 11, trace =FALSE, mse = 'cond', plot=FALSE)
pred.model_5 <- predict(GARCH.model_5, n.ahead = 11, trace =FALSE, mse = 'cond', plot=FALSE)
pred.model_6 <- predict(GARCH.model_6, n.ahead = 11, trace =FALSE, mse = 'cond', plot=FALSE)
predVol_1 <-pred.model_1$standardDeviation
predVol_2 <- pred.model_2$standardDeviation
predVol_3 <- pred.model_3$standardDeviation
predVol_4 <- pred.model_4$standardDeviation
predVol_5 <- pred.model_5$standardDeviation
predVol_6 <- pred.model_6$standardDeviation
et <- abs(rtm.outsample - mean(rtm.outsample))
rtd.HSI.2013 <- rtd.HSI['2013']
rv <- sqrt(aggregate(rtd.HSI.2013^2,by=substr(index(rtd.HSI.2013), 1, 7), sum))
predVol <-round(rbind(predVol_1,predVol_2,predVol_3,predVol_4,predVol_5,predVol_6,
as.numeric(et), as.numeric(rv)), digits=3)
colnames(predVol) <- 1:11
rownames(predVol) <-c('GARCH(1,1)-N模型','GARCH(1,2)-N模型','GARCH(1,1)-t模型','GARCH(1,1)-st模型','GARCH(1,1)-GED模型','GARCH(1,1)-SGED模型','残差绝对值', '已实现波动')
print(predVol)
1 2 3 4 5 6 7 8 9 10 11
GARCH(1,1)-N模型 5.037 5.286 5.513 5.722 5.915 6.094 6.260 6.415 6.560 6.696 6.824
GARCH(1,2)-N模型 4.760 4.747 5.136 5.404 5.661 5.891 6.102 6.296 6.473 6.638 6.789
GARCH(1,1)-t模型 5.347 5.532 5.703 5.864 6.014 6.154 6.286 6.410 6.527 6.638 6.742
GARCH(1,1)-st模型 5.386 5.560 5.722 5.873 6.014 6.146 6.270 6.386 6.495 6.598 6.695
GARCH(1,1)-GED模型 5.168 5.374 5.565 5.741 5.906 6.059 6.203 6.338 6.464 6.583 6.695
GARCH(1,1)-SGED模型 5.229 5.423 5.601 5.767 5.920 6.063 6.197 6.322 6.439 6.548 6.651
残差绝对值 4.147 3.513 3.659 1.464 2.007 7.838 4.584 1.177 4.584 1.026 2.388
已实现波动 3.543 4.114 3.929 4.778 4.374 6.013 5.397 4.634 4.070 3.745 4.395
模型选择
cor(t(predVol))





