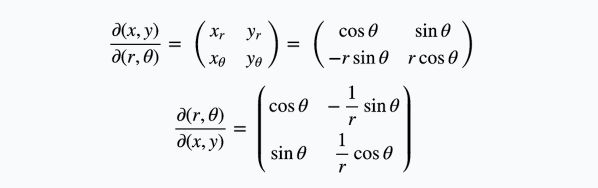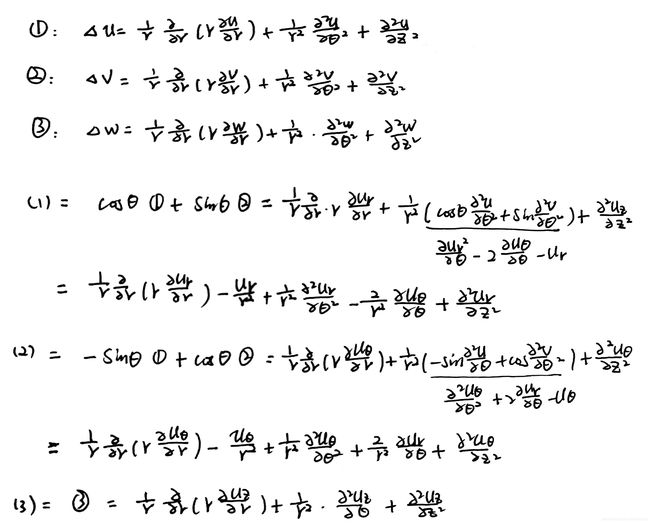柱坐标系下的流体力学控制方程组的微分形式的推导

柱坐标系下的流体力学控制方程组的微分形式的推导

直角坐标系下描述

我们以NS方程（Navier-Stokes Equation）为例，来推导控制方程的柱坐标表示。我这里考虑不可压的，密度和粘性系数都为常数的情况。

此时，直角坐标系下的NS方程的表达形式为，
$$\begin{array}{c}\rho \frac{DV}{Dt}=-\nabla p+\rho g+\mu {\nabla }^{2}V\\ \nabla \cdot V=0\end{array}$$

按分量的形式可以写为：

$$\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=-\frac{\partial P}{\partial x}+\rho g_x+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)$$
$$\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)=-\frac{\partial P}{\partial y}+\rho g_y+\mu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)$$
$$\rho \left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial P}{\partial z}+\rho g_z+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)$$

直角坐标系到柱坐标系

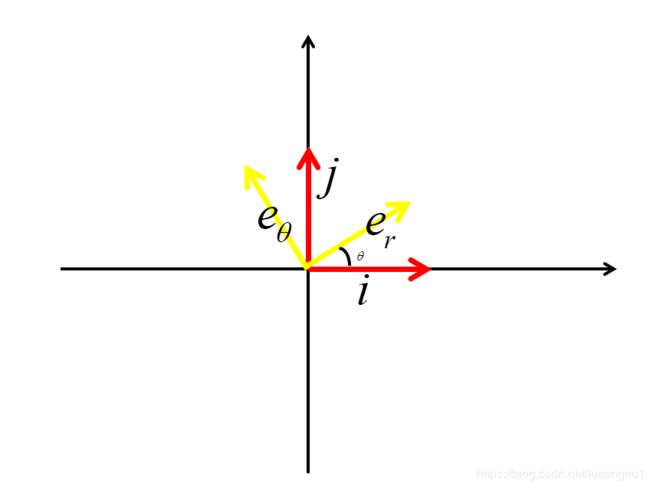
如图所示，我们建立直角坐标系和柱坐标系。

由柱坐标系的定义，我们知道，直角坐标系和柱坐标系满足这样一个关系：

$$\left[\begin{array}{l}r\\ \theta \\ z\end{array}\right]=\left[\begin{array}{c}\sqrt{x^2+y^2}\\ \arctan (y/x)\\ z\end{array}\right],0\le \theta <2\pi$$

$$\left[\begin{array}{l}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}r\cos \theta \\ r\sin \theta \\ z\end{array}\right]$$

假设在直角坐标系中，三个坐标轴方向的单位向量分别表示为$\mathbf{i}、\mathbf{j}、\mathbf{k}$，在柱坐标系中，三个轴向的单位向量表示为${\mathbf{e}}_{\mathbf{r}},{\mathbf{e}}_{\theta },{\mathbf{e}}_{\mathbf{z}}$，那么，如图所示，我们将$\mathbf{i}、\mathbf{j}、\mathbf{k}$分解到柱坐标系中，将${\mathbf{e}}_{\mathbf{r}},{\mathbf{e}}_{\theta },{\mathbf{e}}_{\mathbf{z}}$分解到直角坐标系中，可以得到二者之间的一个关系。

$$\left[\begin{array}{c}{\mathbf{e}}_{\mathbf{r}}\\ {\mathbf{e}}_{\theta }\\ {\mathbf{e}}_{\mathbf{z}}\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}\mathbf{i}\\ \mathbf{j}\\ \mathbf{k}\end{array}\right]$$

$$\left[\begin{array}{l}\mathbf{i}\\ \mathbf{j}\\ \mathbf{k}\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & -\mathrm{s}\mathrm{i}\mathrm{n}\theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\mathbf{e}}_{\mathbf{r}}\\ {\mathbf{e}}_{\theta }\\ {\mathbf{e}}_{\mathbf{z}}\end{array}\right]$$

坐标系变换的雅克比矩阵体现了两个坐标系中变量的偏导关系，表示如下：

柱坐标系下常用算子表示

为了推导不可压NS方程在柱坐标下的表示形式，我们先推导一些常用算子的柱坐标表示（重要但后面不一定全会用到），即：
$$\begin{array}{rl}\nabla f& =\frac{\partial f}{\partial r}{\mathbf{e}}_{\mathbf{r}}+\frac{1}{r}\frac{\partial f}{\partial \theta }{\mathbf{e}}_{\theta }+\frac{\partial f}{\partial z}{\mathbf{e}}_{\mathbf{z}}\\ \nabla \cdot \mathbf{f}& =\frac{1}{r}\frac{\partial }{\partial r}\left(r{f}_r\right)+\frac{1}{r}\frac{\partial f_{\theta }}{\partial \theta }+\frac{\partial f_z}{\partial z}\\ \nabla \times \mathbf{f}& =\left(\frac{1}{r}\frac{\partial f_z}{\partial \theta }-\frac{\partial f_{\theta }}{\partial z}\right){\mathbf{e}}_{\mathbf{r}}+\left(\frac{\partial f_r}{\partial z}-\frac{\partial f_z}{\partial r}\right){\mathbf{e}}_{\theta }+\frac{1}{r}\left(\frac{\partial }{\partial r}\left(r{f}_{\theta }\right)-\frac{\partial f_r}{\partial \theta }\right){\mathbf{e}}_{\mathbf{z}}\\ {\nabla }^{2}f& =\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^{2}f}{\partial {\theta }^2}+\frac{{\partial }^{2}f}{\partial z^2}\end{array}$$

**重要PS：**注意到，这里散度和旋度的定义用到的是的$f$在柱坐标系下的分量来表示，而一阶和二阶梯度中的$f$是一个函数，这个函数既可以在直角坐标系下，也可以在柱坐标系下。

因为Tex公式敲起来挺费事的，我这里只证明一下第一个，其他类似。使用坐标系单位向量之间的关系和链式法则。
$$\begin{gathered} \nabla f=f_x+f_y+f_z=[(f_r\mathrm{c}\mathrm{o}\mathrm{s}\theta -{\mathrm{f}}_{\theta }\frac{1}{\mathrm{r}}\mathrm{s}\mathrm{i}\mathrm{n}\theta )\mathrm{c}\mathrm{o}\mathrm{s}\theta +(f_r\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\mathrm{f}}_{\theta }\frac{1}{\mathrm{r}}\mathrm{c}\mathrm{o}\mathrm{s}\theta )\mathrm{s}\mathrm{i}\mathrm{n}\theta ]{\mathbf{e}}_{\mathbf{r}} \\ +[(f_r\frac{1}{r}\mathrm{c}\mathrm{o}\mathrm{s}\theta -{\mathrm{f}}_{\theta }\frac{1}{\mathrm{r}}\mathrm{s}\mathrm{i}\mathrm{n}\theta )-\mathrm{s}\mathrm{i}\mathrm{n}\theta +(f_r\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\mathrm{f}}_{\theta }\frac{1}{\mathrm{r}}\mathrm{c}\mathrm{o}\mathrm{s}\theta )\mathrm{c}\mathrm{o}\mathrm{s}\theta ]{\mathbf{e}}_{\theta }+f_z{\mathbf{e}}_{\mathbf{z}} \\ =f_r{\mathbf{e}}_{\mathbf{r}}+\frac{1}{r}{f}_{\theta }{\mathbf{e}}_{\theta }+f_z{\mathbf{e}}_{\mathbf{z}} \end{gathered}$$

不可压NS方程柱坐标形式推导

有了上述的工具，我们下一步要做的将Navier-Stokes方程直角坐标表达中的各种算子替换成上述的极坐标表示，整理合并即可。
对于NS方程，对左端求物质导数，NS方程表达为：
$$\rho \frac{\partial V}{\partial t}+\rho V\cdot \nabla V=-\nabla p+\rho g+\mu {\nabla }^{2}V$$

外力项不涉及求导，不发生变换，只要替换相应的变量即可。所以我们只要计算时间导数项，对流项，压强项和粘性项，以及连续性方程。

主要思路

我们想做的事情是，在NS方程的分量表达式

$$\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=-\frac{\partial P}{\partial x}+\rho g_x+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)$$
$$\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)=-\frac{\partial P}{\partial y}+\rho g_y+\mu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)$$
$$\rho \left(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial P}{\partial z}+\rho g_z+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)$$

当中，将$u,v,w$换成$u_r,u_{\theta },u_z$，并且我柱坐标系下的三个式子是关于${\mathbf{e}}_{\mathbf{r}},{\mathbf{e}}_{\theta },{\mathbf{e}}_{\mathbf{z}}$三个方向的分量，即考虑将三个式子做线性组合，左边对左边，右边多右边：
$$\left[\begin{array}{c}柱式1\\ 柱式2\\ 柱式3\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}直式1\\ 直式2\\ 直式3\end{array}\right]$$

考虑直角坐标系向量到柱坐标系的替换：
$$V=\left[\begin{array}{l}u\\ v\\ w\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & -\mathrm{s}\mathrm{i}\mathrm{n}\theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{u}_r\\ u_{\theta }\\ u_z\end{array}\right]$$

将其代入，并利用梯度和拉普拉斯算子在柱坐标下的表示公式（不全用到）：

$$\begin{array}{rl}\nabla f& =\frac{\partial f}{\partial r}{\mathbf{e}}_{\mathbf{r}}+\frac{1}{r}\frac{\partial f}{\partial \theta }{\mathbf{e}}_{\theta }+\frac{\partial f}{\partial z}{\mathbf{e}}_{\mathbf{z}}\\ \nabla \cdot \mathbf{f}& =\frac{1}{r}\frac{\partial }{\partial r}\left(r{f}_r\right)+\frac{1}{r}\frac{\partial f_{\theta }}{\partial \theta }+\frac{\partial f_z}{\partial z}\\ \nabla \times \mathbf{f}& =\left(\frac{1}{r}\frac{\partial f_z}{\partial \theta }-\frac{\partial f_{\theta }}{\partial z}\right){\mathbf{e}}_{\mathbf{r}}+\left(\frac{\partial f_r}{\partial z}-\frac{\partial f_z}{\partial r}\right){\mathbf{e}}_{\theta }+\frac{1}{r}\left(\frac{\partial }{\partial r}\left(r{f}_{\theta }\right)-\frac{\partial f_r}{\partial \theta }\right){\mathbf{e}}_{\mathbf{z}}\\ {\nabla }^{2}f& =\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^{2}f}{\partial {\theta }^2}+\frac{{\partial }^{2}f}{\partial z^2}\end{array}$$

另外链式法则需要用到两个坐标系变换的求导关系：

综上进行合并整理，即可。

连续性方程（质量守恒）

由柱坐标下的散度公式，可知不可压连续性条件为：
$$\frac{1}{r}\frac{\partial \left(r{u}_r\right)}{\partial r}+\frac{1}{r}\frac{\partial \left(u_{\theta }\right)}{\partial \theta }+\frac{\partial u_z}{\partial z}=0$$

时间导数项

因为柱坐标变换是对空间的变换，不涉及时间变量，所以时间导数项在直角坐标系下不发生变化，做一个式分量的线性组合即可。
$$\left[\begin{array}{c}\frac{\partial u_r}{\partial t}\\ \frac{\partial u_{\theta }}{\partial t}\\ \frac{\partial u_z}{\partial t}\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}\frac{\partial u}{\partial t}\\ \frac{\partial v}{\partial t}\\ \frac{\partial w}{\partial t}\end{array}\right]$$

对流项

因为$V$是一个向量，我们可以分别考虑它的每一个分量：

$$\rho V\cdot \nabla f=\rho (\frac{\partial f}{\partial r}u+\frac{1}{r}\frac{\partial f}{\partial \theta }v+\frac{\partial f}{\partial z}w)$$

将$f$分别替换为$u,v,w$，并将其替换为$u_r,u_{\theta },u_z$，合并化简，即可得到对流项。

$$\begin{array}{l}\rho \left(u_r\frac{\partial u_r}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_r}{\partial \theta }-\frac{u_{\theta }^2}{r}+u_z\frac{\partial u_r}{\partial z}\right)\end{array}$$
$$\begin{array}{l}\rho \left(u_r\frac{\partial u_{\theta }}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_{\theta }}{\partial \theta }+\frac{u_r{u}_{\theta }}{r}+u_z\frac{\partial u_{\theta }}{\partial z}\right)\end{array}$$
$$\begin{array}{l}\rho \left(u_r\frac{\partial u_z}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_z}{\partial \theta }+u_z\frac{\partial u_z}{\partial z}\right)\end{array}$$

打tex比较麻烦，将手算稿纸黏贴如下，($\rho$在外面，先不考虑，下同)：

压强项

我们想要的其实就是直角坐标系中的各个分量在柱坐标系下的表达，由前提到的梯度公式，直接可得：

$$-\nabla p=-\frac{\partial p}{\partial r}{\mathbf{e}}_{\mathbf{r}}-\frac{1}{r}\frac{\partial p}{\partial \theta }{\mathbf{e}}_{\theta }-\frac{\partial p}{\partial z}{\mathbf{e}}_{\mathbf{z}}$$

粘性项

$${\nabla }^{2}f=\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial f}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^{2}f}{\partial {\theta }^2}+\frac{{\partial }^{2}f}{\partial z^2}$$

将$f$分别替换为$u,v,w$，做式分量的线性组合，并使用$u_r,u_{\theta },u_z$线性表出替换后并整理，即可。
Tex打起来比较麻烦，手稿如下：

合并

因为等式两边貌似没有一个统一表示的方法，所以最后只能写成分量的形式，最后方程的形式可以写为：
$$\begin{array}{l}\rho \left(\frac{\partial u_r}{\partial t}+u_r\frac{\partial u_r}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_r}{\partial \theta }-\frac{u_{\theta }^2}{r}+u_z\frac{\partial u_r}{\partial z}\right)\\ =-\frac{\partial P}{\partial r}+\rho g_r+\mu \left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_r}{\partial r}\right)-\frac{u_r}{r^2}+\frac{1}{r^2}\frac{{\partial }^2{u}_r}{\partial {\theta }^2}-\frac{2}{r^2}\frac{\partial u_{\theta }}{\partial \theta }+\frac{{\partial }^2{u}_r}{\partial z^2}\right]\end{array}$$

$$\begin{array}{l}\rho \left(\frac{\partial u_{\theta }}{\partial t}+u_r\frac{\partial u_{\theta }}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_{\theta }}{\partial \theta }+\frac{u_r{u}_{\theta }}{r}+u_z\frac{\partial u_{\theta }}{\partial z}\right)\\ =-\frac{1}{r}\frac{\partial P}{\partial \theta }+\rho g_{\theta }+\mu \left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{\theta }}{\partial r}\right)-\frac{u_{\theta }}{r^2}+\frac{1}{r^2}\frac{{\partial }^2{u}_{\theta }}{\partial {\theta }^2}+\frac{2}{r^2}\frac{\partial u_r}{\partial \theta }+\frac{{\partial }^2{u}_{\theta }}{\partial z^2}\right]\end{array}$$

$$\begin{array}{l}\rho \left(\frac{\partial u_z}{\partial t}+u_r\frac{\partial u_z}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial u_z}{\partial \theta }+u_z\frac{\partial u_z}{\partial z}\right)\\ =-\frac{\partial P}{\partial z}+\rho g_z+\mu \left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_z}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^2{u}_z}{\partial {\theta }^2}+\frac{{\partial }^2{u}_z}{\partial z^2}\right]\end{array}$$

不可压连续性条件为：
$$\frac{1}{r}\frac{\partial \left(r{u}_r\right)}{\partial r}+\frac{1}{r}\frac{\partial \left(u_{\theta }\right)}{\partial \theta }+\frac{\partial u_z}{\partial z}=0$$