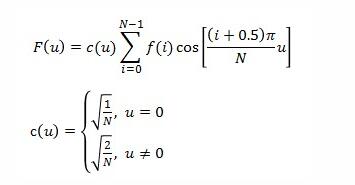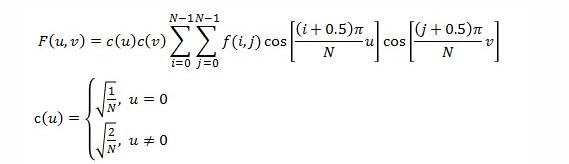DCT变换在图像压缩中的实现

小白拙见，希望理解不对的地方大家多多指教！

对于各种信号，都可以说它是由多个振幅与频率不同的正弦或者余弦函数组成的。并且一个信号通常由一个直流信号DC（幅值保持不变的信号）和多个交流信号AC（幅值以某种频率周期性变化的信号）组成。而通过离散余弦变换（DCT)，就可以将一个源信号分解为DC分量和AC分量，求出它各个分量的系数。
对于DCT来说，其定义为：
一维变换：

二维变换：

首先对于DCT公式里，它有一组基函数，并且这组基函数是正交的，也就是两两互相垂直，就像是三维空间中的x,y，z.比如一维里的cos(2i+1)uπ/16，这就是基函数，并且，随着u取不同的值，我们会得到不同的基函数，例如当u=0时，基函数是cos0=1,这也就说明，这个基函数没有波形变化，他对应的值都是1.但是当我们对u取1时，基函数就是cos(2i+1)π/16，此时，基函数的周期T=2π/（2π/16），周期为16，频率f=1/16.相同的，当u=2，3，4，5，6，7时，频率分别为2/16，3/16，4/16，5/16，6/16，7/16.这说明，这些基函数对应不同的频域，并且从u=0,到u=7,频率是在变大的。而一个源信号f(i）,经过DCT变换，就是将这个源信号包含的这些不同频域的分量给求出来。并且前面说到，一个信号通常由一个DC和多个AC组成，到这里，我们可以看出，在u=0时，求出来的F（0)就是DC分量，其余的u=1,2,3,4,5,6,7时，求出的F（u）是AC分量。
而为什么DCT能把一个信号分解出来不同频域的分量值呢？这就相当于在三维向量中，基向量x（1，0，0）; y(0,1,0) ; z(0,0,1)一样,在三维空间中，任意一个向量A都可以分解为A=ax+by+cz.这里面的x,y，z就是上面的基向量。而我们的DCT中的基向量组跟x,y,z一样，也是正交的，并且可以看出，由于每个基函数的频率不同，所以他们代表着的是不同的频域。通过变换，它也同样可以求出任意一个信号在各个频域上（类似三维空间，也可以说各个基向量方向上）对应的a,b,c......的值，而这些值，就是我们得到的DCT系数了，其中包括一个DC分量和多个AC分量，并且DC分量是代表频率最小的信号，AC1,AC2....AC7对应的是不断增大的频域上的信号。
而如果我们有个图像，我们知道，对于图像来说，其中的边缘，细节上的信号往往是变化比较快，比较剧烈的，所以，图像中的高频信号代表的是图像中的细节和边缘信息。而图像中的大部分内容信息，往往是变换缓慢，频率低的信号，所以，信号中的低频信号代表更多的图像信息。这样，我们就可以通过DCT,求出对应的不同频域分量，最后只保留低频低频，去掉高频数据对应的细节信息，就可以达到压缩的目的了。
例如一个8*8的图像块，其DCT变换后的数据，左上角为低频数据，右下角为高频数据，并且数据能量主要集中在低频区域，即低频区域的值比较大，高频区域的值较小。也就是因为高频区域值小，能量低，所以我们可以在接下来的压缩中，将他们置0，在图片质量看起来影响不大的情况下完成压缩。在这里，我们需要理解一下，为什么低频数据的值就比较大，而高频数据的值比较小呢？首先，对于获得的基函数，低频数值高于高频数值。在设定u=0时，其此时的基函数的取值都等于1，都为正数，如果源信号与此基函数频率相同或相近，那么他们相乘得到的系数将都是相对较大的值，在设定u=1时，其此时的基函数的取值大概为09，0.8，0.5，0.2，-0.2，-0.5，-0.8，-0.9有正数有负数，且绝对值都小于1，那么，对于一个与此信号频率相同的源信号，相乘后的结果较u=0时要小。所以在低频域内得到较大的数值。并且对于一个8*8的图像块非负数据，其最左上角的那个DC值，等于8乘上源信号的平均值；再者，在一般的图像中，低频数据量高于高频数据量，一幅图片中大多数数据，不论是亮度或者是色度，变化都不会很剧烈，所以，低频区域值较大，所占能量更高。

以下是MatlabDCT变换实现：
1、将整个图像整体进行DCT变换：
function [y] = Dct(x)
%图像的DCT变换效果对比
%对整个图片进行DCT变换，观察DCT系数能量分布情况

x=imread(‘Image1.bmp’);
x=rgb2gray(x);%转换成灰度图像
figure(1);imshow(x);title(‘原图’);
y=dct2(x); %计算DCT
figure(2);imshow(log(abs(y)),[]);title(‘DCT系数’);
colormap(gray(4));colorbar;
y(abs(y)<4)=0; %小于4的数值变为0
RD=idct2(y)/255; %反DCT
figure(3);imshow(RD);title(‘恢复图像’);
end

由图可看，DCT系数能量集中在左上方的低频区域。并且对于一些高频数据，我们设置其为0后，图片的还原效果并未受到大的影响。

1、将图像整分成8*8的块进行DCT变换：
function [ y] = DCT_1( x )
%对图像进行分块的DCT变换
% 先将图片进行8*8分块，对每一块进行DCT变换。保留不同数量和部位的DCT系数，对比高频，低频系数对图像质量的影响；
% 将多个块分别反DCT,恢复原图，进行对比
x=imread(‘Image1.bmp’);
x=rgb2gray(x);
x=im2double(x);
t=dctmtx(8);
y = blkproc(x, [8 8], ‘P1 * x * P2’, t, t’);
figure(1);imshow(log(abs(y)),[]);title(‘DCT系数’);
mask1=[1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%保留了3个
mask2=[1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%保留了10
mask3=[1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 0
1 1 1 1 1 0 0 0
1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0];%保留了36
mask4=[ 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1];%保留了全部
mask5=[ 0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1];%保留了右下64-3
mask6=[ 0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 1
0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1];%保留了右下64-10
mask7=[ 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 1
0 0 0 0 0 1 1 1
0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 1
0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1];%保留了右下64-36
y1=blkproc(y,[8 8],’P1.*x’,mask1);
y2=blkproc(y,[8 8],’P1.*x’,mask2);
y3=blkproc(y,[8 8],’P1.*x’,mask3);
y4=blkproc(y,[8 8],’P1.*x’,mask4);
y5=blkproc(y,[8 8],’P1.*x’,mask5);
y6=blkproc(y,[8 8],’P1.*x’,mask6);
y7=blkproc(y,[8 8],’P1.*x’,mask7);

y11=blkproc(y1,[8 8],’P1*x*P2’,t’,t);
y22=blkproc(y2,[8 8],’P1*x*P2’,t’,t);
y33=blkproc(y3,[8 8],’P1*x*P2’,t’,t);
y44=blkproc(y4,[8 8],’P1*x*P2’,t’,t);
y55=blkproc(y5,[8 8],’P1*x*P2’,t’,t);
y66=blkproc(y6,[8 8],’P1*x*P2’,t’,t);
y77=blkproc(y7,[8 8],’P1*x*P2’,t’,t);

figure(2);subplot(2,4,1),imshow(x),title(‘原图’);
figure(2);subplot(2,4,2),imshow(y11),title(‘还原保留左上3’);
figure(2);subplot(2,4,3),imshow(y22),title(‘还原保留左上10’);
figure(2);subplot(2,4,4),imshow(y33),title(‘还原保留左上36’);
figure(2);subplot(2,4,5),imshow(y44),title(‘还原全部’);
figure(2);subplot(2,4,6),imshow(y55),title(‘还原保留右下63-3’);
figure(2);subplot(2,4,7),imshow(y66),title(‘还原保留右下63-10’);
figure(2);subplot(2,4,8),imshow(y77),title(‘还原保留右下63-36’);
end

由DCT系数可以看出，每个数据块的能量集中在左上角处

对比：

通过上面的图片可知，只保留左上角三个数据，就可以得到一个相对完整的图片，而如果保留除左上角三个数据外的其他所有数据，也只得到了一些图像的边缘细节信息。