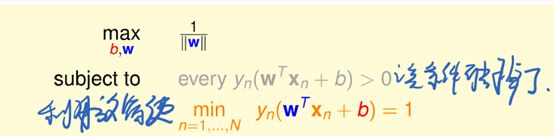《机器学习技法》是国立台湾大学林轩田讲授的一门课程,课程的上集是《机器学习基石》。相关资源可以在youtube找到,也可在评论区索要云盘链接。本文主要是我学完一遍基石&技法后的笔记梳理,如果存疑请以原课程讲授内容为准,欢迎讨论~[注]本文仅适用于帮助复习,不适用于代替视频课程。
技法分为3个部分,分别为
● 核模型:嵌入大量特征(6小节)
● 融合模型:融合预测性特征(5小节)
● 抽取模型:提取隐性特征(4小节)
本文主要梳理第一部分。
一 核模型:嵌入大量特征(6)
1线性SVM(support vector machine支持向量机)
1.1 Fat Hyperplane
1.1.1求距离
去掉绝对值符号:
1.1.2代入Hyperplane公式,
采用某种特殊的比例,将min yn(…)放缩成1,
进一步放宽条件
1.1.3例子
1.2 SVM
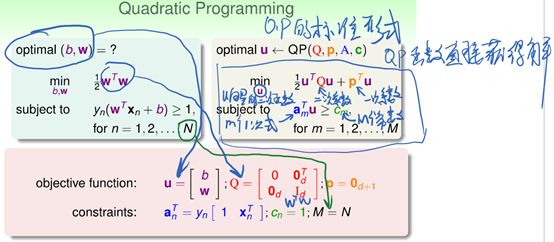
1.2.1二次规划求解
1.2.2线性硬边界SVM算法
1.2.3与regularization的关系
可以看作是一种针对w的regularization
1.2.4优点
1.2.4.1复杂度更小
其中ρ是胖度,d是perceptron的维度(平面上是2D perceptron)
[注]同H的VC dimension指H能shatter几种情况,A的VC dimension指A能shatter几种情况
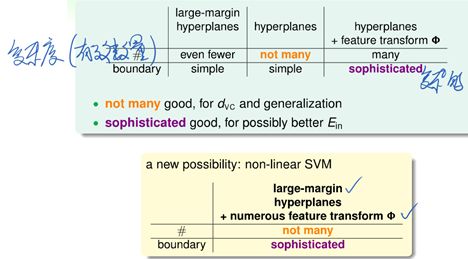
1.2.4.2更好泛化
1.2.4.3可进一步应用于非线性问题
2对偶SVM
2.1 SVM的问题
2.1.1隐藏条件
2.1.2调换max和min
2.1.3对b求偏微分,去掉b
2.1.4对w求偏微分,去掉w
2.1.5求解α
2.1.5.1满足KKT条件才有最优化解
其中原始内部最优时的公式出自2.1.1
2.1.5.2化为标准形式
2.1.5.3使用QP求解器求解α
存在问题:
2.1.5.4反过来求解b和w
2.1.5.5缩小w和b的计算范围
在没有算出w和b之前,我又怎么知道谁是SV呢?αn>0说明(zn,yn)是SV
2.2 VS PLA
2.3 VS原来的SVM
殊途同归。
2.4真的与d无关了吗?
对偶SVM并不能做到与d真正无关,但下一讲的核SVM能够做到。
3核SVM
3.1核函数
Φ2-2表示2次(多项式转换)
3.2运用于SVM,简化q、b、g的计算
3.3 Kernel SVM算法
3.4其它核
3.4.1二次多项式核的一般形式
不同形式的二次多项式核对应同样的空间,但边界会有差异:
3.4.2其它次数多项式核的一般形式
3.4.3高斯核
3.4.3.1高斯核对应无限维的空间
3.4.3.2高斯SVM
3.4.3.3高斯SVM的表现
3.4.4核的选择
3.4.5其它有效的核
核矩阵必须对称、半正定(困难,各阶主子式均≥0)
4软边界SVM
4.1硬边界的缺点
4.2软边界
4.2.1合并条件
4.2.2去掉布尔运算
4.2.3用拉格朗日乘数法去掉条件,转为对偶SVM
4.2.4对ξ求偏微分,去掉ξ和β项
4.2.5对b、w偏微分,去掉w和y项
4.2.6 kernel软边界SVM算法求解α
4.2.7 complementary slackness求解b
[注]αn对数据点n的物理意义
[补充]α=0时,β=C-α=0,ξ≥0条件失效,故SV(α=C)落在边界内。
4.2.8总结
4.3软边界的效果
γ是高斯核的参数,越大边界越尖。C是软SVM的参数,越大越不能容忍杂讯。
4.3.1根据交叉验证做选择
4.3.2根据SV的数量做选择
只有SV作为验证点的时候,会导致err,从而影响Eloocv,故可以依据SV的数量做选择:
5核回归模型
5.1将SVM看作regularized模型
5.1.1 Soft-Margin Primal去条件
5.1.2 VS L2 regularization
不把SVM当作regularization来解是因为它不是QP,不好解,kernel trick用不上。
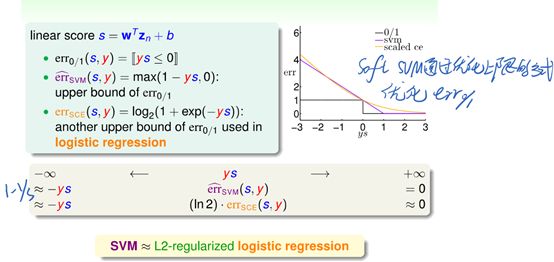
故,无论hard-margin还是soft-margin
SVM的目标函数都很像regularization
把SVM看作普通的regularization,可以启发我们推广到其它模型。
5.2 SVM用于L2范数逻辑回归
5.2.1误差函数的相似性
5.2.2用SVM配合LogReg
用SVM直接获得最终解或者仅用SVM获得一个初始解都不是一个好方法
用SVM获得一个分数(从n维转到了1维),再用这个一维分数来做逻辑回归,最大似然
5.2.2.1 probabilistic(概率的) SVM算法(“两步”算法)
通过这个算法获得了soft binary classifier,但由于B,它的边界会发生变化。
5.2.3用核直接求解LogReg
L2-LogReg能不能用核优化?
证明了L2-regularized linear model可以用kernel trick
5.2.3.1核逻辑回归算法(KLR)(“一步”算法)
5.3用核直接求解岭回归(L2范数线性回归)
通过核岭回归能够直接得到β的解析解,从而得到w*=ΣβZ
5.3.1 VS线性岭回归
一个高效(大数据时),一个灵活(可以做非线性的)
6 SVR(支持向量回归)
6.1 LSSVM的问题(用核岭回归做分类的SVM)
LSSVM的SV太多了
6.2 tube回归
线性回归用平方估错,tube回归用tube估错
6.3 SVR(L2范数-tube回归的标准SVM(反过来的regularization)形式)
L2范数-tube回归
化成标准SVM形式
即为SVR
6.3.1化为对偶形式(用拉格朗日算子去掉条件)
满足KKT条件,有最优化解。
对偶形式:
形式与SVM dual类似,接下来可以用QP求解器求解。
6.3.2 SVR的解是稀疏矩阵
它的SV仅在tube上或tube外
7总结