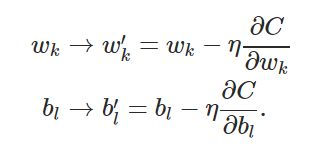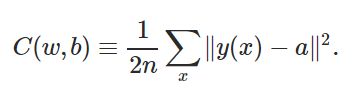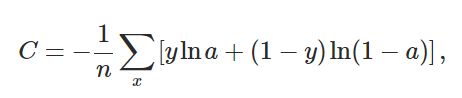sigmoid作为激活函数时使用交叉熵损失函数cross-entropy原由

在大多数使用sigmoid作为激活函数时，神经网络中通过使用交叉熵损失函数cross-entropy可使网络参数能够快速的从错误中学习问题，使梯度下降中权值w以及偏秩b的下降速率得以提升，即可较为快速的得出网络结果。

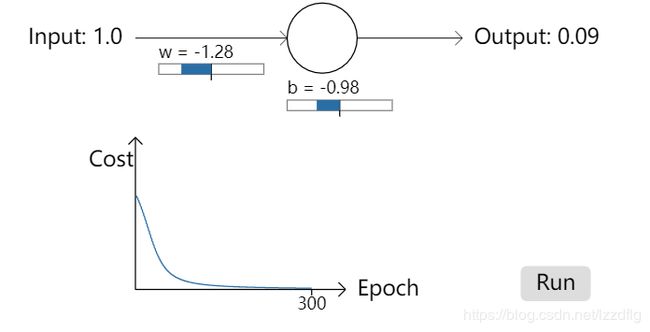
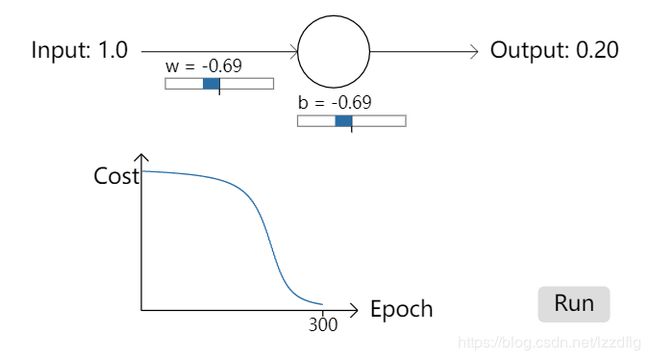
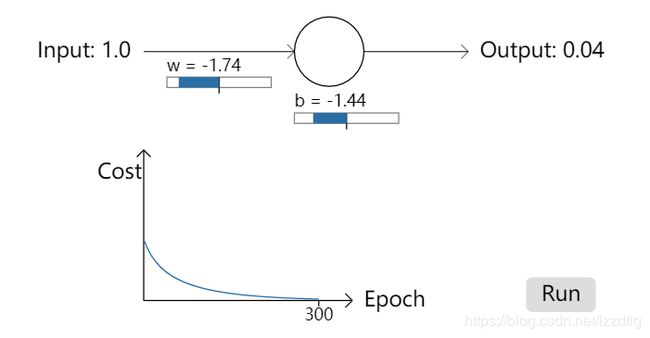
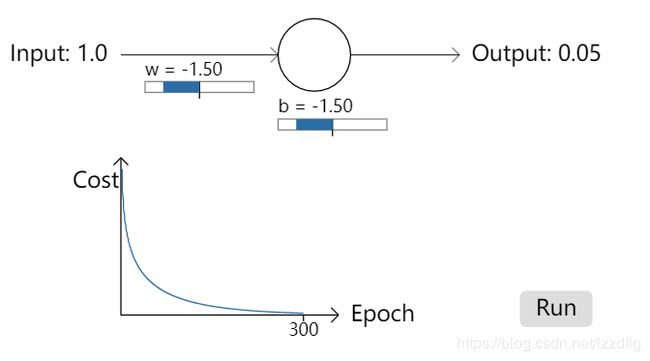
在下方图示中，我们给出神经网络中对于使用sigmoid作为激活函数，在使用二次代价函数(quadratic cost)时产生的一种下降速率缓慢的数据图像。

对于上图两神经网络中，使用quadratic cost损失函数，并分别使用输入数据1.0，1.0，输出数据要求为0.09，0.20，通过查看其w，b值的计算速度，可以得出对于图二情况下，对于前150个左右的学习时期，权重和偏秩根本没有太大变化。为什么会发生如此变化？

其根本原因在于对于权值w和偏秩b，其下降速率由其偏导数 ∂C/∂w 和 ∂C/∂b 决定。

当其偏导数大时，w与b的下降速率快，最终形成神经网络结果时间短。

对于权值w的偏导数，可根据反向传播过程中的4个基本公式

                                                  (1)

                                  (2)

                                                                         (3)

                                                                (4)

其中，

对于公式(1)其内涵为，为损失函数C对于a的偏导（a为神经网络中输入值通过计算到某一神经元时该神经元的值z，经过激活函数优化后的结果）为激活函数的对于z的偏导数。

即对于反向传播中公式（1）对于某L层中第j个神经元。

公式(3)推导过程如下：

                 (5)

因此下降速率大小收到偏导数的影响(公式3，4)。

 

接下来回答为什么对于使用二次代价函数quadratic cost会产生梯度下降缓慢？

对于第l-1层到l层，第l-1层第k个神经元到第l层中第j个神经元。其梯度值：

                 (6)

即对于当使用quadratic cost函数时，其结果会收到sigmoid的影响。从而导致当z接近于1或0时，其sigmoid梯度值接近于0从而导致公式(3)下降速率为0；

为解决其学习速度缓慢问题，通过使用交叉熵损失函数cross-entropy替换原有的quadratic cost损失函数来解决此问题。

交叉熵损失函数

相较于cross-entropy函数，交叉熵损失函数为：

使用交叉熵损失函数可确保下降速率缓慢公式推导

根据图上公式6，通过使用cross-entropy替代quadratic cost导致其改变

以下为改变后推导：

根据将其带入，化简后可得：

由此其梯度值不受sigmoid函数影响，减少了出现梯度下降缓慢的情况。

下图为更改损失函数后的几个测试图像。

 

参考

http://neuralnetworksanddeeplearning.com/chap3.html

CSDN:https://www.cnblogs.com/wlzy/p/7751297.html

 

不是数学系,没那么严谨，可能有地方是错的，但个人理解大概意思是这样。