神经网络中的优化算法
什么是优化算法?
给定一个具有参数θ的目标函数,我们想要找到一个θ使得目标函数取得最大值或最小值。优化算法就是帮助我们找到这个θ的算法。
在神经网络中,目标函数f就是预测值与标签的误差,我们希望找到一个θ使得f最小。
优化算法的种类
一阶优化算法
它通过计算目标函数f关于参数θ的梯度(一阶偏导数)来最小化代价函数。常用的SGD、Adam、RMSProp等基于梯度的优化算法都属于一阶优化算法。
梯度gradient与导数derivative的区别在于,前者用于多变量的目标函数,后者用于单变量的目标函数。
梯度可以用雅克比矩阵表示,矩阵中的每个元素代表函数对每个参数的一阶偏导数。
二阶优化算法
它通过计算目标函数f对参数θ的二阶偏导数来最小化代价函数。常用的有牛顿迭代法。
二阶偏导数可以用Hessian矩阵表示,每个元素都代表函数对每个参数的二阶偏导数。
对比
一阶优化算法只需要计算一阶偏导数,计算更容易
二阶优化算法虽然计算复杂,但是不容易陷入鞍点。
梯度下降法及其变种
在神经网络中,最常用的还是基于下面这种形式的梯度下降法(一阶优化算法):
θ=θ−η⋅∇J(θ)
η 为 learning rate
∇J(θ) 为 代价函数J(θ)对参数θ的梯度
Batch gradient descent
一次参数的更新,需要所有样本都作为输入。样本量太大时容易一下子占满内存,而且不支持online update。
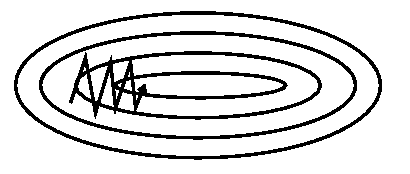
Stochastic gradient descent(SGD)
来一个样本,就执行一次参数更新,计算量大大减少,支持online update。缺点在于参数更新频率太高,参数波动较大,具有高方差(具体解释见文末)。如下图:
learning rate设置过大时容易使参数调节过度。因此使用时一定要保证learning rate不要太大。
Mini Batch Gradient Descent
前两种方法的折中,一次将一个mini batch(通常为50~256个样本)作为输入来执行一次参数更新。优点在于降低了参数更新的高方差;由于使用了mini batch,可以利用向量化编程来提高计算效率。
这是目前神经网络中最为常用的优化方法。
梯度下降法的升级版本
上面的几种方法都有一个共同的缺点:
1.对learning rate的设置较为敏感,太小则训练的太慢,太大则容易使目标函数发散掉。
2.针对不同的参数,learning rate都是一样的。这对于稀疏数据来说尤为不方便,因为我们更想对那些经常出现的数据采用较小的step size,而对于叫较为罕见的数据采用更大的step size。
3.梯度下降法的本质是寻找不动点(目标函数对参数的导数为0的点),而这种不动点通常包括三类:极大值、极小值、鞍点。高维非凸函数空间中存在大量的鞍点,使得梯度下降法极易陷入鞍点(saddle points)且长时间都出不来,如下左图:
注意:
陷入鞍点不代表真的不动了,有的梯度下降法比如SGD或NAG等可以在训练时间足够长后跳出鞍点。如下右图:

Momentum
这个方法是用来解决SGD的参数高幅震荡问题。加速参数在主要方向上的变化,减弱参数在非主要方向上的变化。
参数更新方式:
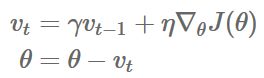
和共轭梯度法的作用类似,通过使用历史搜索方法对当前梯度方向的修正来抵消在非主要方向上的来回震荡。
SGD without momentum

SGD with momentum
motentum方法的缺点主要在于,下坡的过程中动量越来越大,在最低点的速度太大了,可能又冲上坡导致错过极小点。
Nesterov accelerated gradient(NAG)
是对motentum算法进行的改进。给算法增加了预见能力,事先估计出下一个参数处的梯度,用于对当前计算的梯度进行校正。
参数更新:
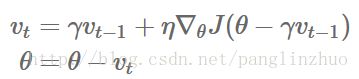
首先沿上一次方向(γvt−1)跨出一大步(brown vector),然后站在那儿计算一下梯度(∇θJ(θ−γvt−1))(red vector),于是,修正过的梯度方向就是γvt−1+η∇θJ(θ−γvt−1)(green vector)
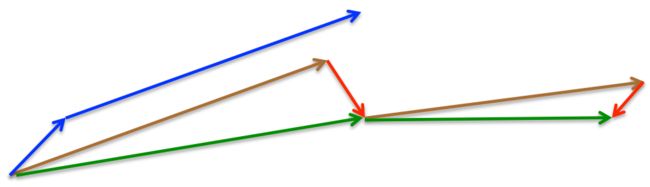
而momentum方法呢?
首先在当前位置计算一下梯度(η∇θJ(θ)),(small blue vector),然后与上次的搜索方向(γvt−1)加起来,迈出了一大步(γvt−1+η∇θJ(θ))(big blue vector)。
Adagrad
首次实现了adaptive learning rate adjustment。也就是不同参数具有不同的学习率。梯度大的参数补偿小一些,梯度小的参数步长大一些。
参数更新方式:
目标函数对每个参数的梯度:
不同于SGD:
Adagrad通过分母项来达到不同参数具有不同学习率的目的:
其中,
可以写成如下的向量化形式:
实验中默认将η设为0.01。
AdaDelta
Adagrad的主要缺点在于,随着时间增长,分母会越来越大,学习率越来越小,学习速度越来越慢。为了解决这个问题,AdaDelta将分母改进为固定时间长度内的梯度平方和。实际操作中,为了使分母可以收敛(不至于无限增大),采用一个dicount factor求出平均的梯度平方和。
参数更新方式为:
由于分母是梯度平方和的均值的平方根(root mean squared——RMS),因此可以写作:
RMSProp
RMSProp是由Hinton发明的,跟AdaDelta基本一样。
通常将η设为0.001
Adam
上面的几种方法都只利用梯度的平方和信息,Adam不仅利用梯度平方和,也利用梯度的和。
第一个公式通过衰减系数β1计算了梯度的平均值。
第二个公式利用衰减系数β2 计算梯度平方的均值。
通常将mt和vt都初始化为零向量。作者发现,由于β1 and β2都是接近于1的衰减系数,mt和vt刚开始总是会接近于0。为了解决这个问题,利用下面的方式对mt和vt进行改进:
思考一下这样为什么有效?
由于衰减系数接近1,分母1−βt1是一个接近0的小数,新的m^t就会在mt的基础上放大好多倍,也就不再容易趋于0了。
这样,参数的更新方式即为:
θt+1=θt−ηv^t−−√+ϵm^t
到底选择哪个方法?
Adam首选,RMSProp次之。
由于NAG的预见能力,它可以比SGD早一步回头是岸
SGD, Momentum, and NAG容易陷入鞍点,RMSprop, Adadelta, and Adam不容易陷入按点。
鞍点
在鞍点处,函数有两个变化方向,一个方向向上,另一个向下:
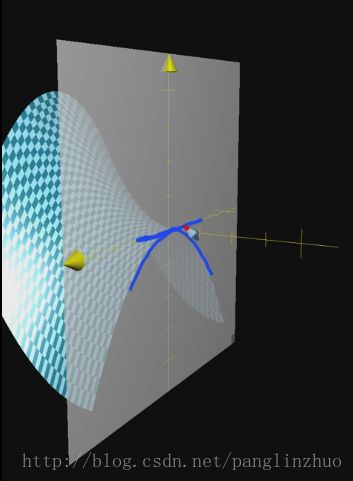
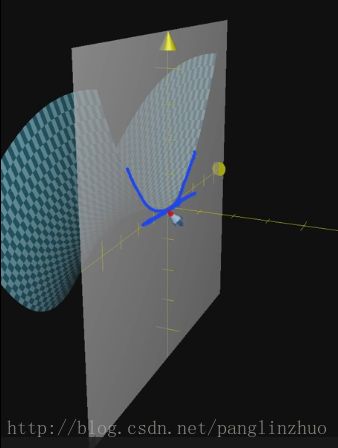
鞍点的判别
检验二元实函数F(x,y)上某一驻点(在该点处函数梯度等于零)是不是鞍点的一个简单的方法,是计算函数在这个点的Hessian矩阵:
如果该矩阵的特征值有正有负,这个矩阵就是不定的,对应的点就是鞍点;
如果矩阵为正定的,这个点就是局部极小值。
bias and variance
machine learning中,整个模型的准确度Error由三部分组成:
Error = bias + variance + noise

bias描述的是训练样本在模型上拟合的好不好:
拟合的好就是low bias,模型就较为复杂,参数较多,容易过拟合,使得测试样本在模型上的预测具有high variance;
拟合的不好就是high bias,模型较为简单,参数较少,容易欠拟合,但是这样的模型由于对数据变化不那么敏感(不管是训练数据或者测试数据都一视同仁),因此在测试样本上的输出具有low variance。
我们既想让模型的训练误差小——low bias——把参数搞的多多的,模型的表达能力就强啦
又想让模型的测试误差小——low variance——参数需要少少的,才能具有更强的(generalization)泛化能力呀
看,bias与variance像不像一对冤家?
参考网址:
1.http://ruder.io/optimizing-gradient-descent/
2.https://medium.com/towards-data-science/types-of-optimization-algorithms-used-in-neural-networks-and-ways-to-optimize-gradient-95ae5d39529f
3.https://www.zhihu.com/question/24258023
4.https://www.zhihu.com/question/52782960/answer/133724696
5.https://zh.wikipedia.org/wiki/%E9%9E%8D%E9%BB%9E
6.https://www.zhihu.com/question/27068705