【算法学习】主席树入门
- 主席树入门
- 原理
- 插入操作
- 未插入数值
- 插入数值4
- 插入数值1
- 查询操作
- 插入操作
主席树入门
主席树,也叫做可持久化线段树,准确来说,应该叫做可持久化权值线段树,因为其中的每一颗树都是一颗权值线段树。
所谓权值线段树,就是指线段树的叶子节点保存的是当前值的个数。这样说起来比较抽象,下面用具体例子来简单阐述。
如有数列:2 1 2 5 1 1 1 3,不难统计出,数列中数字1出现了4次,数字2出现了2次,数字3、数字5都出现了1次,对于这个数列,我们可以说 a[1]=4,a[2]=2,a[3]=1,a[4]=0,a[5]=1 a [ 1 ] = 4 , a [ 2 ] = 2 , a [ 3 ] = 1 , a [ 4 ] = 0 , a [ 5 ] = 1 。如果放在权值线段树种, a[i] a [ i ] 中的下标 i i 不再是对应的数值,而是对应叶子节点的编号了。但是道理是一样的。
为了实现可持久化,就要保存树的历史版本。最自然的想法当然是每进行一次修改,就新建一颗线段树,这样的空间复杂度显然是不能够接受的。通过观察不难发现,每次进行单点修改,发生变化的只有从叶子节点到根节点这一条链上的节点,换句话说,只有 log2n l o g 2 n 个节点发生了变化,而其他的节点都可以重用,没有必要新建。所以有了如下的思路:
每次修改(或插入),新建一个根节点,并且向下递归的新建需要新建的节点。
对于上面这句话,稍作解释:
- 新建根节点是必要的。首先是为了区分不同的版本,修改前是一个版本,修改后是另一个版本。如果做了修改,那么根节点的值一定发生了变化,也必须新建一个根节点。
- 对于新建有不同的理解。自然想到的是去动态的开点,即new一个新的节点,这在ACM中并不是一个很方便的选择,使用不当会造成内存溢出等等问题。所以会选择根据题目的数据范围提前申请好对应变量。所以新建的含义也就变成了为对应的节点分配编号。这在代码中会有更好的体现。
- 关于递归建树,具体实现的方案和普通的线段树很类似,即向左右两个区间递归。区别就在于,由于要用到上一个版本的线段树,如何利用的问题。刚才说过,我们去新建节点,其实就是为节点分配编号,那么问题也即是如何为新的节点分配编号。这里不展开,具体在代码部分进行详细的解释。
以上就是大概主席树的大致描述。下面详细的讲解主席树。
原理
对于主席树的原理,我觉得还是有必要详细的介绍一下。
按照刚才的说法,主席树的关键是对上一版本节点的复用,是如何复用的,下面以主席树经典问题,区间第K大问题来详细的表述。
区间第K大问题,即给定一个数列 a a ,每次询问给定询问的区间 [l,r] [ l , r ] 和想要得到的区间第 K K 大,求返回结果。
如有数列 a=[4,1,3,2] a = [ 4 , 1 , 3 , 2 ] ,有一询问 l=2,r=4,K=2 l = 2 , r = 4 , K = 2 ,观察不难得出答案为 2 2 。
插入操作
在建树时,需要依次将数列中的每个元素插入到树中,每依次插入相当于依次修改,所以每一次插入就要新建一个版本。结合下面的图片,说明一下符号的含义:
Root[i] 表示第i个版本的线段树的根节点编号.
节点左边(或右边) 的数字表示节点的编号.
节点中的数字表示权值(可以理解为区间和).
节点下方的区间表示该节点所维护的区间范围。
未插入数值
插入数值4
我们知道,根节点维护的区间是 [1,4] [ 1 , 4 ] ,根节点右儿子维护的区间是 [3,4] [ 3 , 4 ] ,所以应该向儿子右方向继续递归,知道到叶子节点。并且我们知道上一版本是空树,只有一个根节点,所以没有节点什么可以利用的(请忽略图片中右方的连线!)。
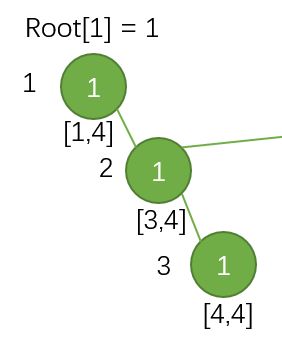
插入数值1
下面插入数值1,根据上面的经验,应该向左子树递归。但是问题是,他的右子树呢?明显插入数值1对其右子树没有发生影响,所以我们将右子树指向上一版本的右子树。指向之后,我们再进入左子树继续递归操作,直到叶子节点。
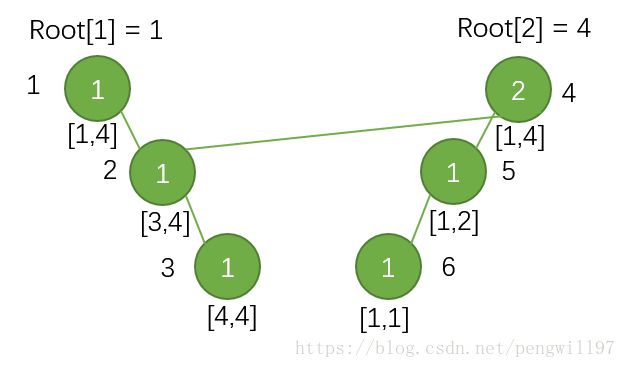
下面的插入操作原理是一样的,不再赘述。
值得提醒的一个地方是,这里所说的指向,并不是用指针,而是将其右子树的域赋值为节点的编号,如在插入数值1后,你可以理解为 tree[root[2]].r=3 t r e e [ r o o t [ 2 ] ] . r = 3 .
查询操作
有了上面的基础,不难看出 tree[root[i]].val t r e e [ r o o t [ i ] ] . v a l 实际上保存的是在第 i i 个版本总共插入了多少个数值。考虑到这是一颗权值线段树。实际上也就是对于题目中所描述的区间,总共插入了多少个数值。现在我们要查询给定数列的 [2,4] [ 2 , 4 ] 的区间第 2 2 大,那么就要用第4个版本和第1个版本做差,求出在这两个版本之间有多少数值。这里的做差,是递归做差,并不是直接将这两棵树的所有节点值域相减,然后在得到的结果树上查找。这样操作很明显耗时间。
首先保证这个区间内要有 K K 个数,否则查询是无意义的。将然后这两个版本树的左子树节点值域做差,得到sum, 如果差值大于等于K,那说明左子树满足查询条件(即左子树有K个数,那么第K大一定在左子树上),就递归去左子树查询第K大;否则就在右子树上,那么我们就去右子树查询第 K−Sum K − S u m 大,为什么是这个数值呢?原因是不要忘记左子树有 Sum S u m 个数,所以要查询 K−Sum K − S u m ,如此递归下去,就可以得到结果。
