深度学习的数学基础(一)线性代数
深度学习的数学基础(一)线性代数
- 1.1 向量
- 向量空间
- 向量的模
- 向量的范数
- 常见向量
- 1.2 矩阵
- 线性映射
- 矩阵操作
- 矩阵类型
1.1 向量
在线性代数中, 标量(Scalar) 是一个实数,而 向量 (Vector) 是指 n个实数组成的有序数组,称为 n维向量。如果没有特别说明,一个 n维向量一般表示列向量,即大小为 n × 1 的矩阵。行在前,列在后,n × 1 则表示n行1列的矩阵,也就是n维向量。
a = [ a 1 a 2 ⋮ a n ] \bf a = \left[ \begin{matrix} a_1 \\ a_2 \\ \vdots \\ a_n \\ \end{matrix} \right] a=⎣⎢⎢⎢⎡a1a2⋮an⎦⎥⎥⎥⎤
其中, a i a_i ai 称为向量 a 的第 i个分量,或第 i维。
为简化书写、方便排版起见,有时会以加上转置符号 T 的行向量(大小为
1 × n 的矩阵)表示列向量。
a = [ x 1 , x 2 , ⋯ , x n ] T \bf a = \left[ \begin{matrix} x_1 , & x_2, & \cdots ,& x_n \\ \end{matrix} \right]^T a=[x1,x2,⋯,xn]T
向量符号一般用黑体小写字母 a , b , c \bf a, b, c a,b,c,或小写希腊字母 α, β, γ 等来表示。
向量空间
向量空间(vector space),也称线性空间(linear space),是指由向量组成的集合,并满足以下两个条件:
- 向量加法 +:向量空间 V 中的两个向量 a \bf a a 和 b \bf b b,它们的和 a + b \bf {a+b} a+b也属于空间 V;
- 标量乘法 ·:向量空间 V 中的任一向量 a \bf a a和任一标量 c,它们的乘积 c · a \bf a a也属于空间 V。
欧氏空间: 一个常用的线性空间是欧氏空间(欧几里德空间)(Euclidean space)。一个欧氏空间表示通常为 R n \mathbb{R^n} Rn,其中n为空间维度(dimension)。欧氏空间中向量的加法和标量乘法定义为:
[ a 1 , a 2 , ⋯ , a n ] + [ b 1 , b 2 , ⋯ , b n ] = [ a 1 + b 1 , a 2 + b 2 , ⋯ , a n + b n ] \left[ \begin{matrix} a_1 , & a_2, & \cdots ,& a_n \\ \end{matrix} \right]+ \left[ \begin{matrix} b_1 , & b_2, & \cdots ,& b_n \\ \end{matrix} \right]= \left[ \begin{matrix} a_1 +b_1, & a_2+b_2, & \cdots ,& a_n +b_n \\ \end{matrix} \right] [a1,a2,⋯,an]+[b1,b2,⋯,bn]=[a1+b1,a2+b2,⋯,an+bn]
c [ a 1 , a 2 , ⋯ , a n ] = [ c a 1 , c a 2 , ⋯ , c a n ] c\left[ \begin{matrix} a_1 , & a_2, & \cdots ,& a_n \\ \end{matrix} \right]= \left[ \begin{matrix} ca_1 , & ca_2, & \cdots ,& ca_n \\ \end{matrix} \right] c[a1,a2,⋯,an]=[ca1,ca2,⋯,can]
其中 a, b∈ R \mathbb{R} R,c为一个标量。
线性子空间 向量空间V 的线性子空间U 是V 的一个子集,并且满足向量空间的条件(向量加法和标量乘法)。
线性无关 线性空间 V 中的一组向量 { v 1 , v 2 , ⋅ ⋅ ⋅ , v n } \{ v_1, v_2, · · · , v_n\} {v1,v2,⋅⋅⋅,vn},如果对任意的一组标量 λ 1 , λ 2 , ⋅ ⋅ ⋅ , λ n λ_1, λ_2, · · · , λ_n λ1,λ2,⋅⋅⋅,λn,满足 λ 1 v 1 , λ 2 v 2 , ⋅ ⋅ ⋅ , λ n v n = 0 λ_1v_1, λ_2v_2, · · · , λ_nv_n=0 λ1v1,λ2v2,⋅⋅⋅,λnvn=0 ,则必然 λ 1 = λ 2 = ⋅ ⋅ ⋅ = λ n = 0 λ_1 = λ_2 = · · · =λ_n = 0 λ1=λ2=⋅⋅⋅=λn=0,那么 { v 1 , v 2 , ⋅ ⋅ ⋅ , v n } \{ v_1, v_2, · · · , v_n\} {v1,v2,⋅⋅⋅,vn}是线性无关的,也称为线性独立的。
线性相关,就是在一组数据中有一个或者多个量可以被其余量表示。线性无关,就是在一组数据中没有一个量可以被其余量表示。从维数空间上讲,例如,一个三维空间,那么必须用三个线性无关的向量来表示,如果在加上另外一个向量,那么这个向量必然可以由上述三个向量唯一的线性表出。在三维空间里,互相垂直的三个坐标轴就是一组最简单的现行无关的向量(其实就是我们下面要说的基向量)。并且是三维空间上的极大无关组。其实,只要是不在同一平面的三个互不平行的向量都可以组成三维空间上的极大无关组。那也就是线性无关的。至于如何理解线性相关和现行无关,其实很简单,举个线性空间上的例子,只要考察这一组向量是否能构成对应维数的线性空间上的极大无关组,也就是说这个维数空间上是否是所有的量都可以通过这组向量表示出。再比如,对一个三维空间,如果有三个向量,并且都在同一平面内,那么这三个向量无法表示出整个三维空间里的所有向量,因为这三个向量是线性相关的。
基向量 向量空间 V 的基(bases) B = { e 1 , e 2 , ⋅ ⋅ ⋅ , e n } B = \{e_1, e_2, · · · , e_n\} B={e1,e2,⋅⋅⋅,en}是 V 的有限子集,其元素之间线性无关。向量空间 V 所有的向量都可以按唯一的方式表达为 B 中向量的线性组合。对任意 v ∈ V,存在一组标量 ( λ 1 , λ 2 , ⋅ ⋅ ⋅ , λ n ) (λ_1, λ_2, · · · , λ_n) (λ1,λ2,⋅⋅⋅,λn)使得
v = λ 1 e 1 + λ 2 e 2 + ⋅ ⋅ ⋅ + λ n e n v = λ_1e_1 + λ_2e_2 + · · · + λ_ne_n v=λ1e1+λ2e2+⋅⋅⋅+λnen
其中基 B 中的向量称为基向量(base vector)。如果基向量是有序的,则标量
( λ 1 , λ 2 , ⋅ ⋅ ⋅ , λ n ) (λ_1, λ_2, · · · , λ_n) (λ1,λ2,⋅⋅⋅,λn)称为向量 v关于基 B 的坐标(coordinates)。
n维空间 V 的一组标准基(standard basis)为
e 1 = [ 1 , 0 , 0 , . . . , 0 ] {\bf e_1}=[1,0,0,...,0] e1=[1,0,0,...,0]
e 2 = [ 0 , 1 , 0 , . . . , 0 ] {\bf e_2}=[0,1,0,...,0] e2=[0,1,0,...,0]
e 3 = [ 0 , 0 , 1 , . . . , 0 ] {\bf e_3}=[0,0,1,...,0] e3=[0,0,1,...,0]
…
e n = [ 0 , 0 , 1 , . . . , 1 ] {\bf e_n}=[0,0,1,...,1] en=[0,0,1,...,1]
V 中的任一向量 v = [ v 1 , v 2 , ⋅ ⋅ ⋅ , v n ] v = [v_1, v_2, · · · , v_n] v=[v1,v2,⋅⋅⋅,vn]可以唯一的表示为
[ v 1 , v 2 , ⋅ ⋅ ⋅ , v n ] = v 1 e 1 + v 2 e 2 + ⋅ ⋅ ⋅ + v n e n [v_1, v_2, · · · , v_n] = v_1e_1 + v_2e_2 + · · · + v_ne_n [v1,v2,⋅⋅⋅,vn]=v1e1+v2e2+⋅⋅⋅+vnen
v 1 , v 2 , ⋅ ⋅ ⋅ , v n v_1, v_2, · · · , v_n v1,v2,⋅⋅⋅,vn 也称为向量 v的笛卡尔坐标(Cartesian coordinates)。
向量空间中的每个向量可以看作是一个线性空间中的笛卡儿坐标。
内积 一个 n维线性空间中的两个向量 a \bf a a 和 b \bf b b ,其内积为
< a , b > = ∑ i = 1 n a i b i <a,b>=\sum_{i=1}^{n}a_ib_i <a,b>=i=1∑naibi
在数学中,数量积(dot product; scalar product,也称为点积)是接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
概括地说,向量的内积(点乘/数量积)。对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,如下所示,对于向量a和向量b:
a = [ a 1 , a 2 , ⋯ , a n ] \bf a=\left[ \begin{matrix} a_1 , & a_2, & \cdots ,& a_n \\ \end{matrix} \right] a=[a1,a2,⋯,an]
b = [ b 1 , b 2 , ⋯ , b n ] \bf b=\left[ \begin{matrix} b_1 , & b_2, & \cdots ,& b_n \\ \end{matrix} \right] b=[b1,b2,⋯,bn]
a和b的点积公式为:
a ⋅ b = a 1 b 1 + a 2 b 2 + . . . + a n b n {\bf a} \cdot {\bf b}=a_1b_1+a_2b_2+...+a_nb_n a⋅b=a1b1+a2b2+...+anbn
两个向量a与b的内积为 a·b = |a||b|cos∠(a, b),特别地,0·a =a·0 = 0;若a,b是非零向量,则a与b正交的充要条件是a·b = 0。
内积(点乘)的几何意义包括:
1.表征或计算两个向量之间的夹角
2.b向量在a向量方向上的投影
正交 如果向量空间中两个向量的内积为 0,则它们正交(orthogonal)。如果向
量空间中一个向量 v 与子空间 U 中的每个向量都正交,那么向量 v 和子空间 U
正交。
向量的模
向量 a 的模就是向量的大小,也就是向量的长度
||a||为: ∣ ∣ a ∣ ∣ = ∑ i = 1 n a i 2 ||\bf a||=\sqrt{\sum_{i=1}^{n}a_i^2} ∣∣a∣∣=i=1∑nai2
向量的范数
在线性代数中, 范数(norm)是一个表示“长度”概念的函数,为向量空间内的所有向量赋予非零的正长度或大小。对于一个n维的向量x,其常见的范数有:
L1范数: ∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||\bf x||_1=\sqrt{\sum_{i=1}^{n}|x_i|} ∣∣x∣∣1=i=1∑n∣xi∣
L2范数: ∣ ∣ x ∣ ∣ 2 = ∑ i = 1 n x i 2 = x T x ||\bf x||_2=\sqrt{\sum_{i=1}^{n}x_i^2}=\sqrt{\bf x^Tx} ∣∣x∣∣2=i=1∑nxi2=xTx
简单理解,范数是表示向量的大小,但是不同的空间,不同的应用场景可以选择不同的衡量方式,
但是向量的模是固定的,就是指欧氏距离。
常见向量
全1向量指所有值为1的向量。用 1 ‾ n \underline1_n 1n表示,n表示向量的维数。 1 ‾ k = [ 1 , ⋅ ⋅ ⋅ , 1 ] K × 1 T \underline1_k = [1, · · · , 1]^T _{K×1} 1k=[1,⋅⋅⋅,1]K×1T
是 K 维的全 1向量。
one-hot 向量表示一个 n维向量,其中只有一维为 1,其余元素都为0。在
数字电路中, one-hot是一种状态编码,指对任意给定的状态,状态寄存器中只有 1位为 1,其余位都为 0。
1.2 矩阵
线性映射
线性映射(linear map)是指从线性空间 V 到线性空间 W 的一个映射函数
f : V → W,并满足:对于 V 中任何两个向量 u和 v以及任何标量 c,有
f ( u + v ) = f ( u ) + f ( v ) f({\bf u} + {\bf v}) = f({\bf u}) + f({\bf v}) f(u+v)=f(u)+f(v)
f ( c v ) = c f ( v ) f(c{\bf v}) = cf({\bf v}) f(cv)=cf(v)
两个有限维欧氏空间的映射函数 f : R n \mathbb{R^n} Rn→ R m \mathbb{R^m} Rm 可以表示为
y = A x ≜ [ a 11 x 1 a 12 x 2 ⋯ a 1 n x n a 21 x 1 a 22 x 2 ⋯ a 2 n x n ⋮ ⋮ ⋱ ⋮ a m 1 x 1 a m 2 x 2 ⋯ a m n x n ] {\bf y}={\bf Ax}\triangleq \left[ \begin{matrix} a_{11}x_1 & a_{12}x_2 & \cdots & a_{1n}x_n \\ a_{21}x_1 & a_{22}x_2 & \cdots & a_{2n}x_n \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}x_1 & a_{m2}x_2 & \cdots & a_{mn}x_n \\ \end{matrix}\right] y=Ax≜⎣⎢⎢⎢⎡a11x1a21x1⋮am1x1a12x2a22x2⋮am2x2⋯⋯⋱⋯a1nxna2nxn⋮amnxn⎦⎥⎥⎥⎤
其中 A定义为 m× n的矩阵(matrix),是一个由 m行 n列元素排列成的矩形阵
列。一个矩阵 A从左上角数起的第 i行第 j 列上的元素称为第 i, j 项,通常记为
[ A ] i j [{\bf A}]_{ij} [A]ij 或 a i j a_{ij} aij。矩阵 A定义了一个从 R n \mathbb{R^n} Rn→ R m \mathbb{R^m} Rm的线性映射;向量 x {\bf x} x ∈ R n \mathbb{R^n} Rn 和 y {\bf y} y ∈ R m \mathbb{R^m} Rm分别为两个空间中的列向量,即 x {\bf x} x大小为 n × 1 的矩阵。 y {\bf y} y大小为 m × 1 的矩阵。
x = [ x 1 x 2 ⋮ x n ] {\bf x}=\left[\begin{matrix} x_1 \\ x_2 \\ \vdots\\ x_n \end{matrix}\right] x=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤
y = [ y 1 y 2 ⋮ y m ] {\bf y}=\left[\begin{matrix} y_1 \\ y_2 \\ \vdots\\ y_m \end{matrix}\right] y=⎣⎢⎢⎢⎡y1y2⋮ym⎦⎥⎥⎥⎤
矩阵操作
加 如果A和B 都为 m × n m × n m×n的矩阵,则A和B 的加也是 m × n m × n m×n的矩阵,其每个元素是 A和 B相应元素相加。
[ A + B ] i j = a i j + b i j [A + B]_{ij} = a_{ij} + b_{ij} [A+B]ij=aij+bij
乘积 假设有两个 A和 B 分别表示两个线性映射 g : R m \mathbb{R^m} Rm → R k \mathbb{R^k} Rk 和 f : R n \mathbb{R^n} Rn → R m \mathbb{R^m} Rm,
则其复合线性映射
( g ◦ f ) ( x ) = g ( f ( x ) ) = g ( B x ) = A ( B x ) = ( A B ) x (g ◦ f)(x) = g(f(x)) = g(Bx) = A(Bx) = (AB)x (g◦f)(x)=g(f(x))=g(Bx)=A(Bx)=(AB)x
其中 A B AB AB 表示矩阵 A A A和 B B B 的乘积,定义为
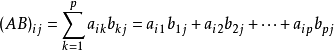
如下所示:

两个矩阵的乘积仅当第一个矩阵的列数和第二个矩阵的行数相等时才能定义。
如 A A A是 k × m k × m k×m矩阵和 B B B 是 m × n m × n m×n矩阵,则乘积 A B AB AB 是一个 k × n k × n k×n的矩阵。
矩阵的乘法满足结合律和分配律:
• 结合律: ( A B ) C = A ( B C ) (AB)C = A(BC) (AB)C=A(BC),
• 分配律: ( A + B ) C = A C + B C (A + B)C = AC + BC (A+B)C=AC+BC, C ( A + B ) = C A + C B C(A + B) = CA + CB C(A+B)=CA+CB.
转置 m × n m × n m×n矩阵A的转置(transposition)是一个 n × m n × m n×m的矩阵,记为 A T A^T AT, A T A^T AT的第 i行第 j列的元素是原矩阵A的第 j行第 i列的元素,
[ A T ] i j = [ A ] j i [A^T]_{ij} = [A]_{ji} [AT]ij=[A]ji.
向量化 矩阵的向量化是将矩阵表示为一个列向量。这里, vec 是向量化算子。
设 A = [ a i j ] m × n A = [a_{ij}]_{m×n} A=[aij]m×n,则
v e c ( A ) = [ a 11 , a 21 , ⋅ ⋅ ⋅ , a m 1 , a 12 , a 22 , ⋅ ⋅ ⋅ , a m 2 , ⋅ ⋅ ⋅ , a 1 n , a 2 n , ⋅ ⋅ ⋅ , a m n ] T vec(A) = [a_{11}, a_{21}, · · · , a_{m1}, a_{12}, a_{22}, · · · , a_{m2}, · · · , a_{1n}, a_{2n}, · · · , a_{mn}]^T vec(A)=[a11,a21,⋅⋅⋅,am1,a12,a22,⋅⋅⋅,am2,⋅⋅⋅,a1n,a2n,⋅⋅⋅,amn]T.
迹 方块矩阵A的对角线元素之和称为它的迹(trace),记为 t r ( A ) tr(A) tr(A)。尽管矩阵的乘法不满足交换律,但它们的迹相同,即 tr(AB) = tr(BA)。
行列式 方块矩阵A的行列式是一个将其映射到标量的函数,记作det(A)或|A|。
行列式可以看做是有向面积或体积的概念在欧氏空间中的推广。在 n维欧氏空
间中,行列式描述的是一个线性变换对“体积”所造成的影响。
秩 一个矩阵 A 的列秩是 A 的线性无关的列向量数量,行秩是 A 的线性无关的行向量数量。一个矩阵的列秩和行秩总是相等的,简称为秩(rank)。
一个m×n的矩阵的秩最大为min(m, n)。两个句子的乘积AB的秩rank(AB) ≤
min( rank(A), rank(B))。
范数 矩阵的范数有很多种形式,其中常用的 ℓp 范数定义为
矩阵类型
对称矩阵 对称矩阵(symmetric)指其转置等于自己的矩阵,即满足 A = A T A = A^T A=AT。
对角矩阵 对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为 0的矩
阵。对角线上的元素可以为 0或其他值。一个 n × n的对角矩阵A满足:
[ A ] i j = 0 i f i ̸ = j ∀ i , j ∈ { 1 , ⋅ ⋅ ⋅ , n } [A]_{ij} = 0 \quad if \ i \not= j \quad ∀i, j ∈ \{1, · · · , n\} [A]ij=0if i̸=j∀i,j∈{1,⋅⋅⋅,n}
对角矩阵 A也可以记为 diag(a), a 为一个n维向量,并满足
[ A ] i i = a i [A]_{ii} = a_i [A]ii=ai
n × n的对角矩阵 A = d i a g ( a ) {\bf A} = diag({\bf a}) A=diag(a)和 n维向量 b \bf b b的乘积为一个 n维向量
A b = d i a g ( a ) b = a ⊙ b {\bf Ab} = diag{\bf (a)b} = {\bf a ⊙ b} Ab=diag(a)b=a⊙b
其中⊙表示点乘,即 ( a ⊙ b ) i = a i b i {\bf (a ⊙ b)}_i = a_ib_i (a⊙b)i=aibi。
单位矩阵(identity matrix)是一种特殊的的对角矩阵,其主对角线
元素为 1,其余元素为 0。 n阶单位矩阵 I n I_n In,是一个 n × n的方块矩阵。可以记
为 I n = d i a g ( 1 , 1 , . . . , 1 ) I_n= diag(1, 1, ..., 1) In=diag(1,1,...,1)。
一个 m × n的矩阵 A和单位矩阵的乘积等于其本身。
A I n = I m A = A AI_n = I_mA = A AIn=ImA=A.
逆矩阵 对于一个 n × n的方块矩阵 A {\bf A} A,如果存在另一个方块矩阵 B {\bf B} B使得
A B = B A = I n {\bf AB = BA = I}_n AB=BA=In
为单位阵,则称 A 是可逆的。矩阵 B 称为矩阵 A 的逆矩阵(inverse matrix),
记为 A − 1 A^{−1} A−1。
一个方阵的行列式等于 0当且仅当该方阵不可逆。
正交矩阵 (orthogonal matrix ) A {\bf A} A为一个方块矩阵,其逆矩阵等于其转置矩阵。
A T = A − 1 {\bf AT = A}^{−1} AT=A−1
等价于 A T A = A A T = I n {\bf A}^T{\bf A} = {\bf AA}^T = {\bf I}_n ATA=AAT=In。