小白学习图像处理——图像的形态学处理（MATLAB）

主要参考《数字图像处理 原理与实践（matlab版）》一书

1、腐蚀

腐蚀在数学形态学运算中的作用是消除物体的边界点。在数字图像处理中，对于确定的结构元素，通过腐蚀运算可以消除小于结构元素的点。同时，若一个目标区域中含有细小的连接部分，那么通过笃实处理可以对区域进行分割。

matlab实现中，需要用到imerode（）和strel（）。

SE=strel(shape,parameters) //参数shape指定了结构元素的形状，parameter指定了输入shape相关的参数

I_result=imerode(I,SE)

shape的取值

 

arbitrary或空	自定义结构元素
disk	圆形
square	正方形
rectangle	长方形
line	线型
pair	包含2个点的结构元素
diamond	菱形
octagon	八角形

matlab代码：

clear;
I=imread('D:\Desktop\TEST.jpg');
SE=strel('disk',10);
im=imerode(I,SE);
figure,imshow(im),title('after erode');

2、膨胀

膨胀中以最大值来判断模板区域内原始图像到底是置于1还是置于0。到对于二值图像，用特定结构的模板去遍历图像上上每一个位置，如果模板特定结构所在位置有一个点为1，则图像上对应特定结构的位置都是1 。对于灰度图像，则是将取1的位置赋值以特定结构重合部位的灰度值的最大值。对于彩色图像则是对三种颜色分量分别进行膨胀处理。

其和腐蚀的最小值相反，在实现中同样适用到strel（）函数，而真正执行的则是imdilate函数。

matlab代码

clear;
I=imread('D:\Documents\Desktop\TEST.jpg');
SE=strel('disk',10);
im=imdilate(I,SE);
figure,imshow(im),title('after erode');

 

图像的背景色对处理的结果影响。个人觉得在白底的时候白色是作为1的填充颜色，毕竟白色是FFFFFF，而黑色是000000，膨胀的时候是取最大值，腐蚀的时候是取最小值，所以会有白底和黑底差异较大的结果。

3、腐蚀和膨胀的关系

设目标图像为A，结构元素为S，用A-S表示对A进行腐蚀运算，用A+S表示对A进行膨胀预算。经推导可得：

（1）对偶性

（2）单调性

（3）递减（增）性

（4）交换律

（5）结合律

（6）平移不变性

（7）各种集合运算

4、腐蚀和膨胀的应用

（1）边界的提取

边界的提取是通过对目标图像进行腐蚀或膨胀处理，比较结果图像和原图像的差别来实现的。

内边界的提取利用图像的腐蚀处理得到原图像的一个收缩，再将收缩结果和目标图像进行异或运算。

外边界的提取对目标图像进行膨胀处理，然后利用膨胀结果与原目标图像进行异或运算。

提取图片内外边界的MATLAB代码

clear;
I=imread('D:\Documents\Desktop\boundary.jpg');
SE=strel('disk',10);
imd=imdilate(I,SE);
ime=imerode(I,SE);
id=imd-I;%计算外边界
ie=I-ime;%计算内边界
subplot(131),imshow(I),title('original image');
subplot(132),imshow(id),title('Outer boundary');
subplot(133),imshow(ie),title('Inner boundary');
figure(2)
subplot(131),imshow(I),title('original image');
subplot(132),imshow(imd),title('膨胀');
subplot(133),imshow(ime),title(' 腐蚀');

 

运行结果

 

5、开运算和闭运算

开运算：A○S=（A-S）+S （即对目标图像先腐蚀再膨胀）

闭运算：A●S=(A+S)-S（即对目标图像先膨胀再腐蚀）

图像的开运算常常用来对木笔哦啊图像进行消噪处理，同时，图像的开运算可以选择性地保留目标图像中符合结构原色几何性质的部分，而过滤掉相对结构元素而言残损的部分。

图像的闭运算常常用来对目标图像分开的区域进行连接及对图像中细小缝隙进行填补，通过适当地选择结构元素，图像的闭运算可以令图像的填补结果具有一点的几何特征，适当地对图像进行闭运算有时可以使图像变得更加清晰连贯，同时可以避免原图像中线条加粗。

matlab代码

clear;
I=imread('D:\Documents\Desktop\kakurablack.jpg');


SE=strel('disk',5);%定义结构元素的形状，圆形-半径5


Iop=imopen(I,SE);%开运算函数，可以直接进行开运算
Icl=imclose(I,SE);%闭运算函数，可以直接进行闭运算
imd=imdilate(I,SE);%只进行膨胀
ime=imerode(I,SE);%只进行腐蚀
imebi=imdilate(imerode(I,SE),SE);%闭运算，先膨胀再腐蚀
imekai=imerode(imdilate(I,SE),SE);%开运算，先腐蚀再膨胀


subplot(241),imshow(I),title('原图');
subplot(242),imshow(ime),title('只腐蚀');
subplot(246),imshow(imd),title('只膨胀');
subplot(245),imshow(I),title('原图');
subplot(243),imshow(Iop),title('开运算函数');
subplot(247),imshow(Icl),title('闭运算函数');
subplot(244),imshow(imekai),title('开运算--先腐蚀再膨胀');
subplot(248),imshow(imebi),title('闭运算--先膨胀再腐蚀');

 

 

白底运行结果

黑底运算结果

6、开运算和闭运算的性质

（1）对偶性

（2）扩展性（收缩性）

（3）单调性

（4）平移不变性

（5）等幂性：在利用开/闭运算进行处理是，处理结果不会因为重复操作而改变。

7、击中/不击中运算

bwhitmiss函数进行的击中击不中运算只能对二值化后的图像进行操作

clear;
I=imread('D:\Documents\Desktop\kakura.bmp');
I2=rgb2gray(I);
thresh = graythresh(I2);     %自动确定二值化阈值；
I3 =  imbinarize(I2,thresh);       %对图像自动二值化即可。
shape1=[0 0 1 0 
       0 0 0 1 ];%自己定义的结构元素1
shape2=[ 0 1 1 0 0
        0 1 1 0 0];%自己定义的结构元素2
imhit=bwhitmiss(I3,shape1,shape2);
    
    SE1=strel('rectangle',[1,3]);%自动生成结构元素长方形
    SE2=strel('disk',5);%自动生成结构元素圆形
    imhit2=bwhitmiss(I3,SE1,SE2);

subplot(221),imshow(I),title('原图');
subplot(222),imshow(imhit),title('击中击不中运算');
subplot(223),imshow(I2),title('灰度图');
subplot(224),imshow(I3),title('二值化');

 

运行结果如下

 

8、图像的细化处理

图像的细化处理是指在保留原图像几何形状的前提下，尽量减少图像所包含的信息量。图像细化的结果被形象的称为图像的骨架。

图像的细化操作实际上是一个逐渐腐蚀的过程，每次从图像的边缘腐蚀掉一个像素，直到不能继续腐蚀位置。

算法的关键是如何在每次腐蚀的过程中判断像素点是否可以清楚。根据不同的需要，可以有不同的准则，基本的两条准则是：①图像的细化不能缩短图像骨架的长度

②细化不能讲图像分解成不同部分

这两条准则在判断是可以总结为一下两点：

①计算当前像素领域内8个方向的可见像素数目，如果少于2个像素，则删除此像素会缩短图像骨架的长度；若多余6个像素，则删除此像素会改变图像骨架的几何形状

②计算大年像素周围领域内的区域数目，如果多余1个，那么删除中信像素会将目标图像分解成不同部分。

与前面的实例不同的是matlab没有直接提供一个专门的函数来实现图像的细化，而是通过一个通用的形态学处理函数bwmorph()来完成，该函数用以实现对二值图像进行一般数学形态学运算的操作。

clear;
I=imread('D:\Documents\Desktop\kakura.bmp');
I2=rgb2gray(I);
thresh = graythresh(I2);     %自动确定二值化阈值；
I3 =  imbinarize(I2,thresh);       %对图像自动二值化即可
img=bwmorph(I3,'thin',inf);
subplot(121),imshow(I),title('原图');
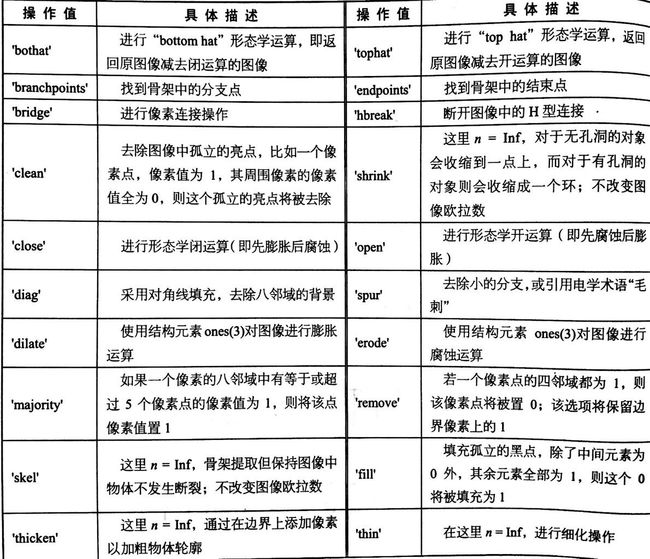
subplot(122),imshow(img),title('细化');

函数bwmorph(image,p,n)的三个参数，第一个image输入的图像，第二个p代表不同的操作方式，第三个n执行操作的次数

①其中image一定是二值图像

②n可以是Inf，即可运行无穷次，直到图像不再发生变化；n也可以缺省，这是主要有p的类型决定；当然可以自己指定具体的操作次数

③p的具体操作见下表