八大排序总结(4)——快速排序(Quick Sort)(c语言实现)
>>>八大排序总结(1)——冒泡排序(Bubble Sort)(c语言实现)<<<
>>>八大排序总结(2)——选择排序(Selection Sort)(c语言实现)<<<
>>>八大排序总结(3)——插入排序(Insertion Sort)(c语言实现)<<<
>>>八大排序总结(5)——归并排序(Merge Sort)(c语言实现)<<<
>>>八大排序总结(6)——希尔排序(Shell Sort)(c语言实现)<<<
>>> 八大排序总结(7)——堆排序(Bubble Sort)(c语言实现)<<<
>>>八大排序总结(8)——线性时间复杂度的排序(桶排序,基数排序,计数排序)【用空间换时间】(c语言实现)<<<
>>>八大排序 时间复杂度,空间复杂度,稳定性的比较<<<
目录
快速排序(Quick Sort)基本思想
原理
时间,空间复杂度与算法稳定性
代码+分析
快速排序(Quick Sort)基本思想
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
原理
分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边(即i=1),指向数字6。让哨兵j指向序列的最右边(即j=10),指向数字8。
首先哨兵j开始出动,因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要(请自己想一想为什么)。哨兵j一步一步地向左挪动(即j--),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。
现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下。
6 1 2 5 9 3 4 7 10 8
到此,第一次交换结束。接下来开始哨兵j继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下。
6 1 2 5 4 3 9 7 10 8
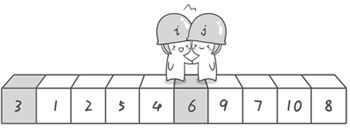
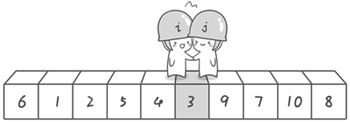
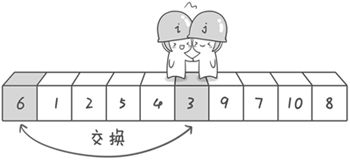
第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下。
3 1 2 5 4 6 9 7 10 8
到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,其实哨兵j的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
OK,解释完毕。现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列。因为6左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列现吧。
左边的序列是“3 1 2 5 4”。请将这个序列以3为基准数进行调整,使得3左边的数都小于等于3,3右边的数都大于等于3。
如果你模拟的没有错,调整完毕之后的序列的顺序应该是。
2 1 3 5 4
OK,现在3已经归位。接下来需要处理3左边的序列“2 1”和右边的序列“5 4”。对序列“2 1”以2为基准数进行调整,处理完毕之后的序列为“1 2”,到此2已经归位。序列“1”只有一个数,也不需要进行任何处理。至此我们对序列“2 1”已全部处理完毕,得到序列是“1 2”。序列“5 4”的处理也仿照此方法,最后得到的序列如下。
1 2 3 4 5 6 9 7 10 8
对于序列“9 7 10 8”也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列,如下。
1 2 3 4 5 6 7 8 9 10
时间,空间复杂度与算法稳定性 
1.时间复杂度:
最坏情况下时间复杂度:O(N^2);
平均时间复杂度:O(NlogN)
2.空间复杂度:O(logN)
3.稳定性:不稳定
代码+分析
void quick_sort(int *a,int left,int right)
{
int i,j,temp;
if (left < right)
{
i = left;
j = right;
temp = a[i];
while (i < j)
{
while (itemp)//向左寻找比temp小的数
j--;
if (i 欢迎大家评论指正,谢谢◕‿◕