matlab遗传算法工具箱的使用

前言：
1.官方文档里面有很多的实例和参数的说明
2.图形化操作之后可以自动生成代码
3.注意在程序里面要关掉打开的文件 fclose

内容提要

启用：

遗传算法：
在ga.m的文档中其实有很多例子
1.
 A = [1 1; -1 2; 2 1];  b = [2; 2; 3];  lb = zeros(2,1);
%    % Use mutation function which can handle constraints
    options = optimoptions('ga','MutationFcn',@mutationadaptfeasible);
    [x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb,[],[],options);

2.
  fun = @(x) (x(1) - 0.2)^2 + (x(2) - 1.7)^2 + (x(3) -5.1)^2; 
 x = ga(fun,3,[],[],[],[],[],[],[],[2 3])

3.匿名函数
 x = ga(@(x) 3*sin(x(1))+exp(x(2)),2)

 4.官方文档
 function [x,fval,exitFlag,output,population,scores] = ga(fun,nvars,Aineq,bineq,Aeq,beq,lb,ub,nonlcon,intcon,options)
 function [解，适应度值，退出标志，输出，种群大小，得分]=ga(函数，解的维数，不等式的系数A，不等式的系数b，等式的系数A，等式的系数b)
 
%GA    Constrained optimization using genetic algorithm.
%   GA attempts to solve problems of the following forms:
%       min F(X)  subject to:  A*X  <= B, Aeq*X  = Beq (linear constraints)
%        X                     C(X) <= 0, Ceq(X) = 0 (nonlinear constraints)
%                              LB <= X <= UB 
%                              X(i) integer, where i is in the index
%                              vector INTCON (integer constraints)
%
%   Note: If INTCON is not empty, then no equality constraints are allowed.
%   That is:-
%   * Aeq and Beq must be empty
%   * Ceq returned from NONLCON must be empty
%
%   X = GA(FITNESSFCN,NVARS) finds a local unconstrained minimum X to the
%   FITNESSFCN using GA. NVARS is the dimension (number of design
%   variables) of the FITNESSFCN. FITNESSFCN accepts a vector X of size
%   1-by-NVARS, and returns a scalar evaluated at X.
%
%   X = GA(FITNESSFCN,NVARS,A,b) finds a local minimum X to the function
%   FITNESSFCN, subject to the linear inequalities A*X <= B. Linear
%   constraints are not satisfied when the PopulationType option is set to
%   'bitString' or 'custom'. See the documentation for details.
%
%   X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq) finds a local minimum X to the
%   function FITNESSFCN, subject to the linear equalities Aeq*X = beq as
%   well as A*X <= B. (Set A=[] and B=[] if no inequalities exist.) Linear
%   constraints are not satisfied when the PopulationType option is set to
%   'bitString' or 'custom'. See the documentation for details.
%
%   X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub) defines a set of lower and
%   upper bounds on the design variables, X, so that a solution is found in
%   the range lb <= X <= ub. Use empty matrices for lb and ub if no bounds
%   exist. Set lb(i) = -Inf if X(i) is unbounded below;  set ub(i) = Inf if
%   X(i) is unbounded above. Linear constraints are not satisfied when the
%   PopulationType option is set to 'bitString' or 'custom'. See the 
%   documentation for details.
%
%   X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub,NONLCON) subjects the
%   minimization to the constraints defined in NONLCON. The function
%   NONLCON accepts X and returns the vectors C and Ceq, representing the
%   nonlinear inequalities and equalities respectively. GA minimizes
%   FITNESSFCN such that C(X)<=0 and Ceq(X)=0. (Set lb=[] and/or ub=[] if
%   no bounds exist.) Nonlinear constraints are not satisfied when the
%   PopulationType option is set to 'bitString' or 'custom'. See the 
%   documentation for details.
%
%   X = GA(FITNESSFCN,NVARS,A,b,Aeq,beq,lb,ub,NONLCON,options) minimizes
%   with the default optimization parameters replaced by values in OPTIONS.
%   OPTIONS can be created with the OPTIMOPTIONS function. See OPTIMOPTIONS
%   for details. For a list of options accepted by GA refer to the
%   documentation.
%
%   X = GA(FITNESSFCN,NVARS,A,b,[],[],lb,ub,NONLCON,INTCON) requires that
%   the variables listed in INTCON take integer values. Note that GA does
%   not solve problems with integer and equality constraints. Pass empty
%   matrices for the Aeq and beq inputs if INTCON is not empty.
%
%   X = GA(FITNESSFCN,NVARS,A,b,[],[],lb,ub,NONLCON,INTCON,options)
%   minimizes with integer constraints and the default optimization
%   parameters replaced by values in OPTIONS. OPTIONS can be created with
%   the OPTIMOPTIONS function. See OPTIMOPTIONS for details.
%
%   X = GA(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a structure
%   that has the following fields:
%       fitnessfcn: 
%            nvars: 
%            Aineq: 
%            bineq: 
%              Aeq: 
%              beq: 
%               lb: 
%               ub: 
%          nonlcon: 
%           intcon: 
%          options: 
%         rngstate: 
%
%   [X,FVAL] = GA(FITNESSFCN, ...) returns FVAL, the value of the fitness
%   function FITNESSFCN at the solution X.
%
%   [X,FVAL,EXITFLAG] = GA(FITNESSFCN, ...) returns EXITFLAG which
%   describes the exit condition of GA. Possible values of EXITFLAG and the
%   corresponding exit conditions are
%
%     1 Average change in value of the fitness function over
%        options.MaxStallGenerations generations less than 
%        options.FunctionTolerance and constraint violation less than 
%        options.ConstraintTolerance.
%     3 The value of the fitness function did not change in
%        options.MaxStallGenerations generations and constraint violation 
%        less than options.ConstraintTolerance.
%     4 Magnitude of step smaller than machine precision and constraint
%        violation less than options.ConstraintTolerance. This exit 
%        condition applies only to nonlinear constraints.
%     5 Fitness limit reached and constraint violation less than
%        options.ConstraintTolerance. 
%     0 Maximum number of generations exceeded.
%    -1 Optimization terminated by the output or plot function.
%    -2 No feasible point found.
%    -4 Stall time limit exceeded.
%    -5 Time limit exceeded.
%
%   [X,FVAL,EXITFLAG,OUTPUT] = GA(FITNESSFCN, ...) returns a
%   structure OUTPUT with the following information:
%             rngstate: 
%          generations: 
%            funccount: 
%        maxconstraint: , if any
%              message: 
%
%   [X,FVAL,EXITFLAG,OUTPUT,POPULATION] = GA(FITNESSFCN, ...) returns the
%   final POPULATION at termination.
%
%   [X,FVAL,EXITFLAG,OUTPUT,POPULATION,SCORES] = GA(FITNESSFCN, ...) returns
%   the SCORES of the final POPULATION.
%
%
%   Example:
%     Unconstrained minimization of 'rastriginsfcn' fitness function of
%     numberOfVariables = 2
%      x = ga(@rastriginsfcn,2)
%
%     Display plotting functions while GA minimizes
%      options = optimoptions('ga','PlotFcn',...
%        {@gaplotbestf,@gaplotbestindiv,@gaplotexpectation,@gaplotstopping});
%      [x,fval,exitflag,output] = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options)
%
%   An example with inequality constraints and lower bounds
%    A = [1 1; -1 2; 2 1];  b = [2; 2; 3];  lb = zeros(2,1);
%    % Use mutation function which can handle constraints
%    options = optimoptions('ga','MutationFcn',@mutationadaptfeasible);
%    [x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb,[],[],options);
%
%     FITNESSFCN can also be an anonymous function:
%        x = ga(@(x) 3*sin(x(1))+exp(x(2)),2)
%
%   If FITNESSFCN or NONLCON are parameterized, you can use anonymous
%   functions to capture the problem-dependent parameters. Suppose you want
%   to minimize the fitness given in the function myfit, subject to the
%   nonlinear constraint myconstr, where these two functions are
%   parameterized by their second argument a1 and a2, respectively. Here
%   myfit and myconstr are MATLAB file functions such as
%
%        function f = myfit(x,a1)
%        f = exp(x(1))*(4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + a1);
%
%   and
%
%        function [c,ceq] = myconstr(x,a2)
%        c = [1.5 + x(1)*x(2) - x(1) - x(2);
%              -x(1)*x(2) - a2];
%        % No nonlinear equality constraints:
%         ceq = [];
%
%   To optimize for specific values of a1 and a2, first assign the values
%   to these two parameters. Then create two one-argument anonymous
%   functions that capture the values of a1 and a2, and call myfit and
%   myconstr with two arguments. Finally, pass these anonymous functions to
%   GA:
%
%     a1 = 1; a2 = 10; % define parameters first
%     % Mutation function for constrained minimization
%     options = optimoptions('ga','MutationFcn',@mutationadaptfeasible);
%     x = ga(@(x)myfit(x,a1),2,[],[],[],[],[],[],@(x)myconstr(x,a2),options)
%
%   Example: Solving a mixed-integer optimization problem
%   An example of optimizing a function where a subset of the variables are
%   required to be integers:
%   
%   % Define the objective and call GA. Here variables x(2) and x(3) will
%   % be integer. 
%   fun = @(x) (x(1) - 0.2)^2 + (x(2) - 1.7)^2 + (x(3) -5.1)^2; 
%   x = ga(fun,3,[],[],[],[],[],[],[],[2 3])
%          
%   See also OPTIMOPTIONS, FITNESSFUNCTION, GAOUTPUTFCNTEMPLATE, PATTERNSEARCH, @.

%   Copyright 2003-2015 The MathWorks, Inc.

% If the first arg is not a gaoptimset, then it's a fitness function followed by a genome
% length. Here we make a gaoptimset from the args.

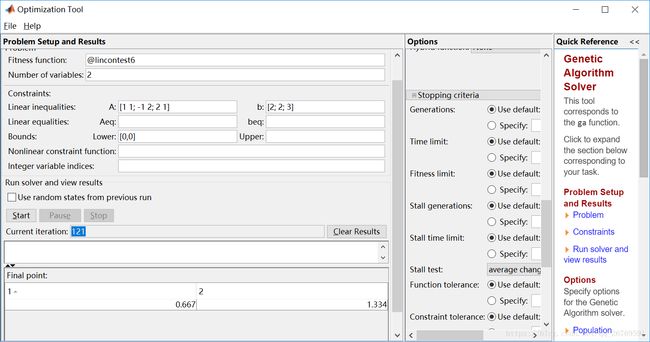
遗传算法的调用方式和参数的说明

可以这样查看默认参数的值

A = [1 1; -1 2; 2 1]; 
b = [2; 2; 3];  lb = zeros(2,1);  
[x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb)
注意顺序决定传值

遗传算法简单的几个测试用例

遗传算法测试用例
1.分段函数测试
%分段函数测试 ok
function y=ga_f_test(x)
y=0;
if x>1
    y=y+x;
else
    y=y+2*y;
end
end


2.关于解的测试，我觉得解应该只能是一维的

2.
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];  
lb = zeros(2,1);  
[x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb)  
%lb表示x的下界，up表示上界 
 Optimization terminated:   
 average change in the fitness value less than   
 options.TolFun.    
 x =     0.7794   1.2205    
 fval =-8.03916    exitflag =

谈谈我使用遗传算法过程中的一些坑
1.遗传算法只能生成一维的向量做为解 所以参数栏只会让你输入一个个数
2.那些参数的意义 可以见上面的
3.遗传算法适合各各样的问题，不论你的函数里面是分段的还是提前退出的，可以使用return 但是要注意的是退出的时候最好是个一个较大的随机值，而不是一个固定的值，否则最后会认为解基本上没有变化，然后就终止掉了

        if x(i)==x(j)  %一旦发现重复的值 给他一个很大的值然后马上退出
          distance=randi(1000)*100000 ;    

4.对于这种离散的点，其实可以先给点编号，然后随机生成1-6之间的数，再根据序号进行读值，这样可提高效率，保证有解
5.如何控制不生成重复的解目前还只能通过自己的程序进行控制

%控制一下不能有重复的值 
for i=1:Number_of_trash   
    for j=i+1:Number_of_trash 
        if x(i)==x(j)  %一旦发现重复的值 给他一个很大的值然后马上退出
          distance=randi(1000)*100000 ;    
         return ;
        end    
    end
   
end

最后贴上自己的完整的代码

dis2

 

function distance=dis2(x)
%准备数据
%x=[1 2 3 4 5 6];
input = importfile('input.txt');
Num_of_obstacle=input{3:3,{'VarName1'}};
trash=zeros(1,3);
Number_of_trash=input{3+Num_of_obstacle+1:3+Num_of_obstacle+1,{'VarName1'}};
for i=1:Number_of_trash
    trash_temp=input{3+Num_of_obstacle+1+i:3+Num_of_obstacle+1+i,{'VarName1','VarName2','VarName3'}};
    trash(:,:,i)= trash_temp;
    w(i)=trash_temp(1,3);
end
%把垃圾读进来
robot=input{2:2,{'VarName1','VarName2','VarName3','VarName4'}};
garbage=input{3+Num_of_obstacle+Number_of_trash+2:3+Num_of_obstacle+Number_of_trash+2,{'VarName1','VarName2'}};
w_temp=0;
weight=5;
distance=0;


%控制一下不能有重复的值 
for i=1:Number_of_trash   
    for j=i+1:Number_of_trash 
        if x(i)==x(j)  %一旦发现重复的值 给他一个很大的值然后马上退出
          distance=randi(1000)*100000 ;    
         return ;
        end    
    end
   
end


 
for i=1:Number_of_trash   
   %每到达一个点 首先计算距离和权重
   w_temp=w_temp+ trash(1,3,x(i));
   %若没有超重
    if w_temp1
                  distance=distance+abs(trash(1,1,x(i))-trash(1,2,x(i-1)))+abs(trash(1,1,x(i))-trash(1,1,x(i-1)));
                end  %i1
            end  %i==Number_of_trash
        end  %i==1
    else  %若是超重
       %先把之前的放下，只计算当前一个的重量
       w_temp=0;
       w_temp=w_temp+ trash(1,3,x(i));
       %这里默认第一个永远都不是超重的 所以就不会陷入死循环
       %距离=到达的距离+扔垃圾的距离
       if i>1
       distance=abs(trash(1,1,x(i-1))-garbage(1,1))+abs(trash(1,2,x(i))-garbage(1,2))+abs(trash(1,1,x(i))-garbage(1,1))+abs(trash(1,2,x(i))-garbage(1,2))+distance;        
       else   %第一个垃圾就大于 weight 直接退出  一般情况下这是不可能存在的
        distance=inf;
        return
       end 
       end
 
end

ga_dis2

function [x,fval,exitflag,output,population,score] = ga_dis2()
%% This is an auto generated MATLAB file from Optimization Tool.
nvars=6;
lb=[1 1 1 1 1 1];
ub=[6 6 6 6 6 6];
intcon=[1 2 3 4 5 6];
FunctionTolerance_Data=1e-6;
ConstraintTolerance_Data=1e-3;
%% Start with the default options
options = optimoptions('ga');
%% Modify options setting
options = optimoptions(options,'FunctionTolerance', FunctionTolerance_Data);
options = optimoptions(options,'ConstraintTolerance', ConstraintTolerance_Data);
options = optimoptions(options,'Display', 'off');
[x,fval,exitflag,output,population,score] = ...
ga(@dis2,nvars,[],[],[],[],lb,ub,[],intcon,options);