强化学习论文(5): Learning Latent Dynamics for Planning from Pixels

Google Brain，Deepmind 提出的 PlaNet
论文地址：https://danijar.com/publications/2019-planet.pdf
源码地址：https://github.com/google-research/planet

摘要

planning（规划）对已知环境转移动态的控制任务非常成功，如需在未知环境中使用 planning，则 agent 需要通过环境交互学习转移动态。然而，学到足够精确支持 planning 的转移动态模型是一项长期挑战，特别是在图像领域。
本文提出 Deep Planning Network (PlaNet)，是一个model-based agent，能够：

1. 从图像中学习环境转移动态；
2. 通过在隐空间进行快速在线 planning 来选择动作。

要实现高性能，转移动态模型必须能精确预测多个时间步之后的 reward。为达成这一目标，本文使用了一个隐动态模型，包含确定性和随机性组件。同时，本文还提出了一个多步变分推断目标，记为 latent overshooting.
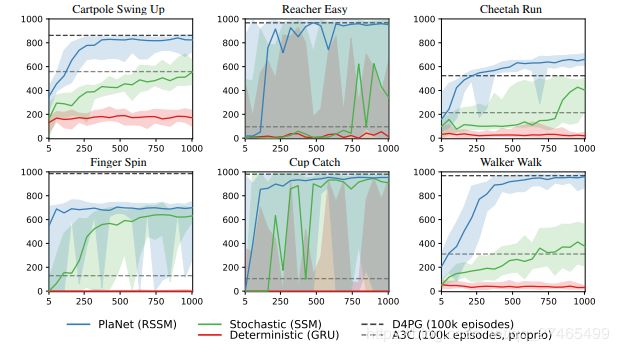
本文所提出的 agent 仅使用像素观察，来解决部分可观测，稀疏 reward 的控制问题，超出了以往 model-based方法解决问题的难度。其表现与 model-free 方法相当，而样本量更少。

背景介绍

学习转移动态模型最主要的困难包括：模型的准确性，多步预测累积的误差，未能捕获未来丰富的可能性，以及对训练分布的过拟合造成的泛化失败。
使用学习得到的模型进行 planning，相比 model-free 方法有以下几点好处：

1. model-based planning 方法更加 data-efficient（数据依赖小），因为它对训练信号的使用更充分，并且不需要通过贝尔曼方程传递 reward；
2. 以增加对 action 的搜索为计算代价，planning 提高了agent 的表现
3. 学到的模型独立于特定任务，有潜力通过转化服务于相同/似环境下的其他任务。

近期的工作已经展示了在简单低维情形下学习转移动态的优势，但这些工作都假定已知环境的底层状态和明确的reward函数，这在现实应用中并不可行。在高维情形下，我们希望在一个紧凑的隐空间学习转移动态以保证快速 planning。这种隐空间模型已经在简单任务上取得了成功。
一句话总结：PlaNet 发展了model-based planning 方法，解决了更困难的基于像素的连续控制问题。
主要贡献：潜空间planning，循环状态空间模型，latent overshooting（给出多步预测变分下界，改善多步预测结果）.

潜空间planning

Framework

假设已有学到的转移动态模型，算法框架如下：
由于单一图像无法反映环境状态的全部信息，将问题建模为一个POMDP（部分可观测 markov 决策过程），$s_t$为底层状态，$o_t$为环境观测，$a_t$为连续动作向量。

注意到PlaNet所有的建模都只针对环境，而后在环境中进行规划，并没有策略网络/值网络。同时，在交互过程中，每一步都重新做planning，以保证能够根据新的观测作出调整（与MPC类似）。

Planning 算法

Planning算法使用了CEM (cross entropy method), CEM是一种基于群体的优化方法，它能够推断出动作序列的最优分布。

模型

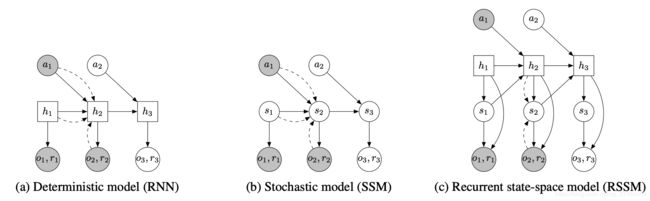
本文提出一个循环状态空间模型 (RSSM) 在隐空间进行前向预测，这一模型可被看作非线性Kalman滤波器或者序列VAE.

SSM

潜状态空间模型如下图b所示，下面所涉及的模型都是由神经网络参数化的高斯分布。


由于模型都是非线性的，因此无法直接计算出参数学习所需的状态后验。因此，本文使用编码器 $q\left(s_{1:T}|o_{1:T},a_{1:T}\right)={\prod }_{t=1}^{T}q\left(s_t|s_{t-1},a_{t-1},o_t\right)$来从过去的观测和动作中近似推断状态后验，其中$q\left(s_t|s_{t-1},a_{t-1},o_t\right)$是一个由“卷积网络+前向网络”参数化的对角高斯分布。
为使用编码器，本文建立了一个基于数据对数似然的变分下界 (Jensen 不等式)：
$\ln p\left(o_{1:T}|a_{1:T}\right)\triangleq \ln \int {\prod }_{t}p\left(s_t|s_{t-1},a_{t-1}\right)p\left(o_t|s_t\right)d{s}_{1:T}\ge {\sum }_{t=1}^T\left(\underset{\text{ reconstruction }}{{\mathrm{E}}_{q\left(s_t|o_{\le t},a_{<t}\right)}\left[\ln p\left(o_t|s_t\right)\right]}-\underset{\text{ complexity }}{{\mathrm{E}}_{q\left(s_{t-1}|o_{\le t-1},a_{<t-1}\right)}\left[\mathrm{K}\mathrm{L}\left[q\left(s_t|o_{\le t},a_{<t}\right)\Vert p\left(s_t|s_{t-1},a_{t-1}\right)\right]\right]}\right).$
推导比较简单，包含重要性采样和Jensen不等式的使用两个步骤，包含在附录中，关于变分下界的推导也可参考变分自编码器VAE(Variational Autoencoders)及示例代码。使用重参数化技巧保证了随机梯度下降可以顺利使用。

RSSM

尽管随机模型具有很强的泛化能力，然而，纯粹的随机模型难以记住多个时间步骤所包含的信息。理论上，某些情况下策略方差可以设置为0（确定性策略），然而上述优化过程难以收敛到这类结果。这促使本文引入了一个确定性激活向量序列 ${\left\{h_t\right\}}_{t=1}^T$ 允许模型确定地访问所有先前的状态。于是就有了本文所使用的模型 RSSM，如上图c所示。

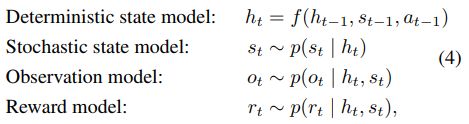
其中$f\left(h_{t-1},s_{t-1},a_{t-1}\right)$是一个RNN。直观地，我们可以理解为该模型将状态划分为一个随即部分$s_t$和一个确定状态$h_t$，它们由之前时间步的随即部分和确定部分决定。本文使用编码器$q\left(s_{1:T}|o_{1:T},a_{1:T}\right)={\prod }_{t=1}^{T}q\left(s_t|h_t,o_t\right)$来参数化近似状态后验。

Latent Overshooting

Motivation

在上一部分，本文建立了在隐序列空间进行学习和推断的标准变分下界，包含一个针对观测的重构项和一个针对近似后验的KL散度正则项。这个变分推断目标的一个缺陷是：转移概率函数$p\left(s_t|s_{t-1},a_{t-1}\right)$的随机部分仅被KL正则中的单步预测所训练，梯度经过$p\left(s_t|s_{t-1},a_{t-1}\right)$后直接进入$q(s_{t-1})$，而不进入$p\left(s_{t-1}|s_{t-2},a_{t-2}\right)$从而遍历多个$p(s_{t_i})$. 在这一部分，我们将标准变分下界推广到 latent overshooting，可在潜空间训练所有的多步预测。
事实上，如果模型能够做完美的单步预测，那么它也能做出完美的多步预测。然而，通常使用的模型都容量有限并且限制在确定的分布族上，将模型单步训练至收敛，与多步预测所需的最佳模型并不一致。成功规划需要精确的多步预测，并在所有的多步预测数据上训练模型。本文把这一想法推广到潜序列模型，表明多步预测也可以被潜空间上的loss来优化，而不需要添加额外的图像。

固定距离$d$的多步预测

我们开始把上面训练单步预测的标准变分下界推广到固定距离$d$的多步预测情形。为省略起见，省略了$s_t$关于$a_t$的先验。则：
$$\begin{array}{rl}p\left(s_t|s_{t-d}\right)& \triangleq \int \prod _{\tau =t-d+1}^{t}p\left(s_{\tau }|s_{\tau -1}\right)d{s}_{t-d+1:t-1}\\ & ={\mathrm{E}}_{p\left(s_{t-1}|s_{t-d}\right)}\left[p\left(s_t|s_{t-1}\right)\right]\end{array}$$
于是，关于多步预测分布 $p_d$ 的变分下界为：
$\ln p_d\left(o_{1:T}\right)\triangleq \ln \int {\prod }_{t=1}^{T}p\left(s_t|s_{t-d}\right)p\left(o_t|s_t\right)d{s}_{1:T}\ge {\sum }_{t=1}^T\left(\underset{\text{ reconstruction }}{{\mathrm{E}}_{q\left(s_t|o_{\le t}\right)}\left[\ln p\left(o_t|s_t\right)\right]}-\underset{\text{ multi-step prediction }}{{\mathrm{E}}_{p\left(s_{t-1}|s_{t-d}\right)q\left(s_{t-d}|o_{\le t-d}\right)}\left[\mathrm{K}\mathrm{L}\left[q\left(s_t|o_{\le t}\right)\Vert p\left(s_t|s_{t-1}\right)\right]\right]}\right)$
推导和上一部分类似，最大化这一目标就能使多步预测的准确性得到训练。这一反应了在多步预测中，模型无需访问先前的所有观测，仅在潜空间就可进行预测。

Latent overshooting：可变距离多步预测

Latent overshooting就是再把多步预测变分下界从固定$d$步推广到$1\le d\le D$:
$\frac{1}{D}{\sum }_{d=1}^D\ln p_d\left(o_{1:T}\right)\ge {\sum }_{t=1}^T\left(\underset{\text{ reconstruction }}{{\mathrm{E}}_{q\left(s_t|o_{\le t}\right)}\left[\ln p\left(o_t|s_t\right)\right]}-\underset{\text{ latent overshooting }}{\frac{1}{D}\sum _{d=1}^D{\beta }_d{\mathrm{E}}_{p\left(s_{t-1}|s_{t-d}\right)q\left(s_{t-d}|o_{\le t-d}\right)}\left[\mathrm{K}\mathrm{L}\left[q\left(s_t|o_{\le t}\right)\Vert p\left(s_t|s_{t-1}\right)\right]\right]}\right)$
Latent overshooting 可以被看作潜空间的正则项，鼓励单步和多步预测之间的一致性，因为这两者在数据集上的期望应该是相等的。同时引入了权重因子$\{{\beta }_d{\}}_{d=1}^D$，可以被调整来决定是更多关注短期预测还是长期预测。

对比

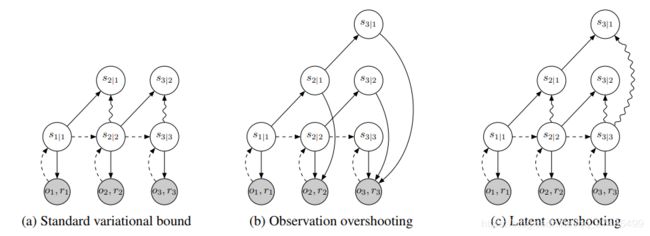
如上图所示，a为标准变分下界，包含下方的重构loss，和上方单步预测的KL正则；b为观测overshooting，将潜空间展开预测多步重构loss，但是在图像领域计算代价过于昂贵；c可以看作以上两者的结合和扩展。
从附录结果看，latent overshooting 对于 RSSM 提升不显著，对于确定性模型可能意义更大。

实验