【论文笔记2】图像压缩神经网络在Kodak数据集上首次超越JPEG——Full Resolution Image Compression with Recurrent Neural Networks
一、引言
Google Research的George Toderici以及他的团队,在提出基于LSTM的卷积/反卷积RNN图像压缩网络框架的第二年,发表了这篇文章。论文传送门:《Full Resolution Image Compression with Recurrent Neural Networks》。他们提出的上一篇论文中的LSTM卷积/反卷积网络框架是理解本篇论文的基础,我的【论文笔记1】讲的就是这篇论文,想要了解的请戳此传送门:【论文笔记1】RNN在图像压缩领域的运用——Variable Rate Image Compression with Recurrent Neural Networks;原论文传送门:《Variable Rate Image Compression with Recurrent Neural Networks》。
这篇论文提出了一种基于神经网络的全分辨率的有损图像压缩方法,在变压缩比的情况下无需重复训练,所以说整个网络只需要训练一次。论文的内容主要包括如下三个部分:
(1)提出了三种图像压缩框架,分别是基于LSTM的RNN网络、基于关联LSTM(associative LSTM)的RNN网络和结合GRU结构和ResNet残差训练思想的基于残差输入GRU的RNN网络。三种网络都由编码网络、二值化网络、解码网络和熵编码网络四部分构成。
(2)研究比较了三种图像重建的架构,分别是“one-shot”、“additive reconstruction”和新的“residual scaling”方法。
(3)采用熵编码进一步提高图像压缩比。熵编码技术已经广泛应用在了标准图像压缩算法中。
本文提出的网络最终在AUC(area under the rate-distortion curve,即率失真曲线下的面积,表示图像失真度与编码率二者之间的关系)上相较于已有的图像压缩方法的性能提高了4.3%至8.8%,并且是应用在Kodak数据集在,无需熵编码,在大部分比特率的率失真曲线上超越JPEG的第一个图像压缩神经网络框架。
二、已有图像压缩方法的缺点与本文的改进
现有的标准图像压缩算法例如JPEG等和标准自编码器模型的缺点在我的【论文笔记1】中都有阐述,在这里不在赘述。
上一篇论文(即我在【论文笔记1】中讲的George Toderici团队于2016年发表的论文)中提出的基于LSTM的卷积/反卷积RNN图像压缩网络存在两个很大的缺点:
(1)图像的大小只能为32×32;
(2)没有考虑图像patch之间的长期依赖性。
为了使网络可以在压不同缩比范围内压缩任意大小的图像,文章提出了如下两种解决方案:
(1)设计一个性能更强的基于图像patch的残差编码器;
(2)设计一个熵编码器来抓取图像patch之间的长期依赖性。
为了描述提出的网络结构的性能,文章不仅使用PSNR、Lp差异这两个传统指标,还引入了PSNR-HVS和MS-SSIM这两个常用的矩阵来评价网络的压缩性能。
三、本文提出的方法
1、方法综述
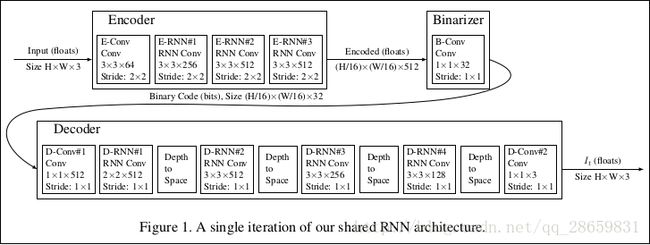
本文提出的网络结构的单步流程如下图所示:
网络包含编码器E、二值化网络B和解码器D三个部分,编码器E将图片编码成representation code,二值化网络将representation code变换成二值化编码,解码器通过二值化编码预测输入的原始图片。将原始图片和解码器预测图片之间的残差作为下一步迭代的输入循环迭代过程,网络的权重在不同迭代过程中是共享的。所以,单步迭代过程可以用如下方程表示:
![]()
![]()
Dt和Et分别表明第t步迭代时刻的解码器和编码器状态,bt是具有连续性的二值化representation编码,xt尖是重构的图片。当gamma=0的时候表示的是“one-shot”重构,gamma=1时表示的是“additive”重构,这将在后文提到。
二值化网络使用的方法和上一篇论文的方法一样,在k步迭代后,网络会生成共计m×k比特的二值化编码,m是每一步迭代生成的二值化编码比特数。对于32×32的图片patch,m=128。
形成网络编码器和解码器的递归单元含有两种不同的卷积核,一个是作用在来自上一层的输入向量上的,一个是作用在状态向量上的,将作用在状态向量上的卷积叫做隐卷积,将作用在状态向量上的卷积核叫做隐卷积核。对于输入向量的卷积可是实现完全的深度方向上的卷积操作,例如D-RNN#3有256个卷积核作用输入向量上,每一个卷积核空间尺寸为3×3,在深度上实现完全卷积(128,因为一个“Depth-to-Space”操作将图片深度降低四倍)。除了D-RNN#3和D-RNN#4的隐卷积核是3×3以外,其它的卷积操作的隐卷积核都是1×1,因为实验证明,相较于上一篇论文的隐卷积核全为1×1,大的隐卷积核可以提高网络的压缩性能。
训练过程中,网络的损失函数是带权重的每一步的残差加和,表示如下:
网络的每一步迭代将每一个32×32×3的输入图片经过编码和二值化网络生成一个2×2×32的二值化representation,因此每部迭代bbp为1/8,如果只用第一步迭代,那么即使不用熵编码,网络的压缩比也能达到192:1。
2、三种不同的递归单元结构
文章提出了三种不同的递归单元结构,分别是LSTM、关联LSTM和结合GRU结构和ResNet残差训练思想的基于残差输入GRU的RNN网络。
2.1 LSTM
LSTM的结构可以用如下方程表示:
![]()
![]()
![]()
![]()
其中xt、ct、ht分别代表的是输入、LSTM单元状态和隐层状态,下标代表的是迭代时间节点,圆圈内加一点代表的是元素级别的乘法,b是偏置;W和U分别代表对输入向量的卷积和对状态向量的隐卷积,需要注意的是W卷积和U卷积应该有相同的深度。
2.2 关联LSTM(Associative LSTM)
关联LSTM使用全息representation代替LSTM,它的结构可以用如下方程表示:
![]()
![]()
![]()
![]()
ht加上波浪号表示的是关联LSTM在t时刻的输出。实验证明,仅在解码器中使用关联LSTM的效果更好,因此文章中的基于关联LSTM网络都是只用解码器中使用关联LSTM单元而编码器中依然使用非关联的LSTM单元。
2.3 残差输入的GRU
GRU(Gated Recurrent Units),是LSTM的一个变体,当然LSTM还有有很多其他的变体。GRU保持了LSTM的效果同时又使结构更加简单,所以它也非常流行。(GRU的解释来自博客http://blog.csdn.net/wangyangzhizhou/article/details/77332582)
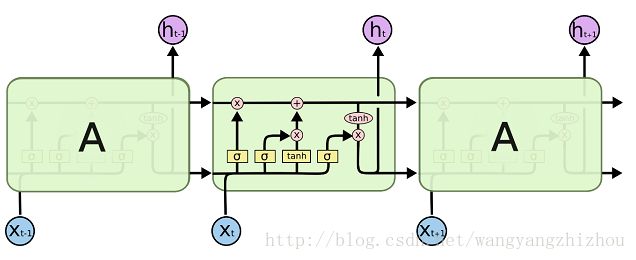
回顾一下LSTM的模型,LSTM的重复网络模块的结构很复杂,它实现了三个门计算,即遗忘门、输入门和输出门。
而GRU模型如下,它只有两个门了,分别为更新门和重置门,即图中的zt和rt。更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门用于控制忽略前一时刻的状态信息的程度,重置门的值越小说明忽略得越多。
GRU单元的结构可用如下方程表示:
![]()
![]()
![]()
文章还受到了ResNet和Highway Networks的启发,将残差信息加入GRU的输入以加速收敛。最终,残差输入GRU单元的结构可用如下方程表示:
![]()
![]()
文章在试验中将αx和αh都设置成了0.1。
3、图片重构的框架
文章研究比较了三种图像重建的架构,分别是“one-shot”、“additive reconstruction”和“residual scaling”方法。
3.1 One-shot reconstruction
回顾一下在方法总数中提到的论文提出的网络框架的单步迭代过程,它的方程为:
![]()
![]()
当图像重建过程中γ=0时,即每一步解码器都在预测整个图像。随着迭代进行下去,通过编码得到的representation的比特数越来越多,因此重建的图片质量便越来越好,这种方法被称为one-shot重建方法。尽管每一步都在预测原始图片,但是每一步只将上一步的残差信息传递给下一层,实验证明,这种方式重建的图像效果并不好。这和上一篇论文中提出的不基于LSTM的网络的使用的重建方法相同。
3.2 Additivie reconstruction
当γ=1时,每一步迭代都是在利用上一层的残差预测新的残差,最终的图片重建过程是通过加和所有迭代过程的残差得到的。这和上一篇论文中提出的基于LSTM的网络使用的重建方法相同。
3.3 Residual scaling reconstruction
以上两种重建原图像的方法都存在一个缺点,就是图片的残差在初始的时候是非常大的,理论上是期望残差随着迭代的进行越来越小,而实际上编码器和解码器很难在很大的数值范围内高效执行。此外,残差的收敛速率是内容独立的,意思就是,对于一张图片patch可能它收敛得很快,而另外一张图片可能就会很慢了。
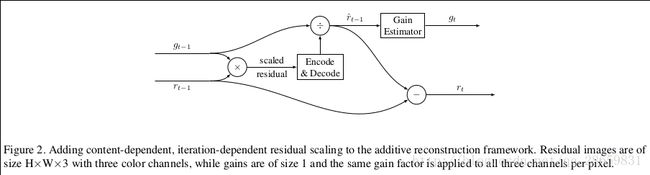
因此,文章为了解决以上两种问题,提出了一种新的图片重构方法:Residual scaling reconstruction。这种方法将加和重构的方法扩展,引入了内容独立系数和迭代独立系数。Residual scaling重构方法的图解如下:
Residual scaling重建方法关注上一轮迭代过程预测的残差,残差通过与上一轮gain estimator的输出scale系数相乘得到一个scaled的残差。scaled residual经过编码和解码后预测了一个新的残差,该残差通过gain estimator得到新的scale系数,当前迭代过程的残差由上一轮的残差和本轮预测的残差相减得到。整个residual scaling的结构可用如下方程表示:
![]()
![]()
![]()
![]()
![]()
![]()
其中圆圈中加斜杠表示元素等级的除法;ZOH表示零阶保持器上采样;G表示scale系数的估计函数,它由五层前向卷及神经网络构成,每层的卷积步长为2,前四层卷积核尺寸为3×3,使用ELU非线性函数,输出深度为32,最后一层使用2×2卷积核和ELU非线性函数使得输出深度为1。此外为了保证ELU的输出为(1,+∞),ELU的输出加上常数2(因为ELU的非线性化值域为(-1,+∞))。
实验证明,Residual scaling重建方法解决了重建过程中的残差内容独立的问题,具有更好的图片重建效果。
4、熵编码
4.1 熵编码原理
熵编码技术已经广泛地用在标准图像压缩算法中,使用熵编码技术可以进一步提高图像的压缩比,因为之前的网络都不是专门为了最大化熵而设计的。熵编码即编码过程中按熵原理不丢失任何信息的编码。信息熵为信源的平均信息量(不确定性的度量)。熵编码是一种无损压缩,例如一幅图像,每个像素用一个字节表示,分析每个像素值出现的概率,把出现概率大的值用少于一个字节的字符表示,而出现概率小的值用多于一个字节字符表示,这样平均每个像素所占的大小就少于一个字节,从而达到压缩图像的目的。常见的熵编码有:香农编码、霍夫曼编码和算数编码等。JPEG图像编码标准采用的熵编码算法就是霍夫曼编码。
按照香农提出的信息论的观点,把数据看做信息和冗余度的结合。所谓冗余指一幅图像的像素之间存在着很大的相关性,可以利用一些编码的方法山区,从而达到减少冗余压缩数据的目的。
熵的定义如下:设信息源S=S1,S2,S3,...,Sn,Si出现的概率为Pi,1≤i≤N,则信息源的熵为:
根据香农信息论,无论规定的码字符如何编排,其平均的码字符所占用的位数不可能小于原符号表达的熵值。那么信息的最大离散熵为:
则最大熵和熵之间的差值成为冗余度:
![]()
这就意味着,只要信息源不是等概率分布的,就存在这数据压缩的可能。即编码后字符的平均码长L与信源的熵H(s)可以任意接近。
后文关于论文的熵编码方法,目前还有一些没理解的问题,待学习理解后更新补充。
4.2 单步迭代熵编码
文章中的熵编码其实就是用一个网络框架求概率P(C|T),然后通过求P(C|T)和P尖(C|T)的交叉熵来确定编码c(y,x,d)的最理想的长度,从而进一步压缩编码长度,提高压缩比。
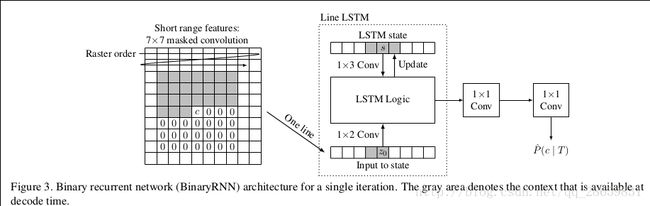
单步迭代压缩上编码包含三个步骤,图示结构如下:
(1)一个卷积核尺寸为7×7的卷积用来提高LSTM的感受野;
(2)卷积后的结果按行输入进入LSTM模块;
(3)两个1×1的卷积用来增加网络记忆容量。
最后,单步迭代的交叉熵的计算公式为:
4.3 多歩迭代熵编码
在多歩迭代的过程中,每一步迭代都重复单步迭代的熵编码过程,但是每次迭代过程的LSTM不能只有当前过程的输入,这样无法抓取迭代过程间的冗余信息。因此,在多步迭代过程中,LSTM不在仅仅接收当前的卷积输出z0还会接收上一次迭代过程的信息z1,其中z1由上一步的编码经过多个卷积和一个LSTM卷积过程得到。如下图所示:
5、结果与分析
文章测试了4种编码解码单元{GRU, Residual GRU, LSTM, Associative LSTM}×3种图像重建方法{One Shot Reconstruction, Additive Reconstruction, Additive Rescaled Residual},共12种模型,并与上一篇论文的结果(记为Baseline)相比较。文章开源了代码并提供了详细的实验流程。实验流程请戳此传送门:Supplymentary Materials;代码请戳:https://github.com/tensorflow/models/tree/f87a58cd96d45de73c9a8330a06b2ab56749a7fa/research/compression(不支持训练);Pytorch复现代码:https://github.com/1zb/pytorch-image-comp-rnn。
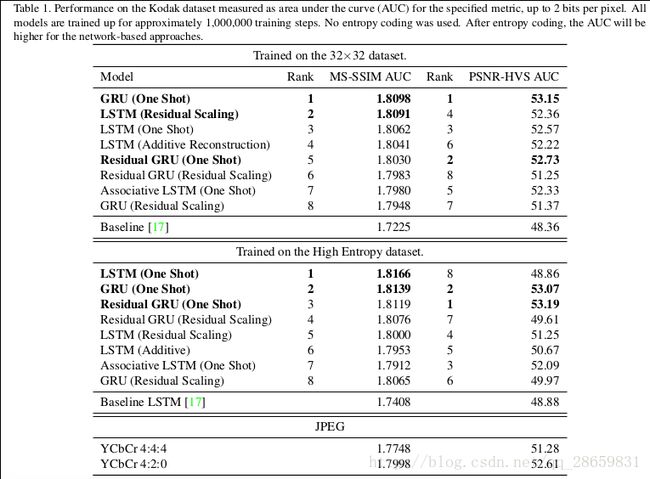
在未经过熵编码操作的模型结果如下:
由表格可以看出,在没有熵编码的情况下,在32×32的图像数据集中,one-shot重建法的残差GRU模型在MS-SSIM和PSNR-HVS两个指标上均取得了最好的效果;在高信息熵的数据集中,one-shot重建法的LSTM模型在MS-SSIM指标上取得了最好的结果,one-shot重建法的Residual GRU在PSNR-HVS指标上表现最好。
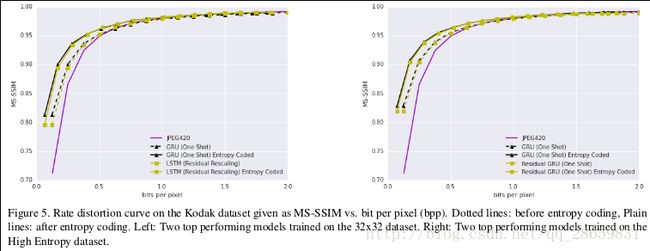
然而,加上额外的熵编码后,模型在Kodak数据集上的提升很小,比特率最多只有在2bpp时提升5%到在0.25bpp时提升32%,因为该数据集中大多是相对低分辨率的图像,而熵编码主要对大图像的压缩起显著作用。结果如下图所示:
综上所述,文章应用了4种不同的编码解码单元和3种图像重构方法提出了4×3=12种图像压缩RNN框架,并在MS-SSIM和PSNR-HVS指标上进行了测试,平均程度上来说已经超越了JPEG。并且证明了熵编码可以抓取编码中的冗余信息,进一步降低编码长度,提高压缩比。
-------------------------------------------
Youzhi Gu, master student
Foresight Control Center
College of Control Science & Engineering
Zhejiang University
Email: [email protected]