四元数表示旋转的理解

哈密尔顿

为了纪念四元数的发明者哈密尔顿,爱尔兰于1943年11月15日发行了下面这张邮票:
哈密尔顿简直是个天才,哈密尔顿从小到进入大学之前没有进过学校读书，他的教育是靠叔父传授以及自学。他找到了法国数学家克莱罗（Clairaut）写的《代数基础》一书，很快就学会了代数，然后看牛顿写的《数理原理》。在16岁时就读法国著名数学家和天文学家拉普拉斯（Laplace）五册的《天体力学》，他发现拉普拉斯关于力的平行四边形法则的证明的错误.
四元数的概念是由爱尔兰数学家Sir William Rowan Hamilton发明的（1843年，都柏林）。Hamilton当时正和他的妻子前往爱尔兰皇家研究院，当他从Brougham桥通过皇家运河时，他领悟到了一个激动人心的东西，并立刻把它刻在桥的一个石头上：

i2=j2=k2=ijk=−1 i 2 = j 2 = k 2 = i j k = − 1

关于哈密尔顿的介绍可以看这篇博客: 邮票上的数学家(10)哈密尔顿(爱尔兰)

---

四元数旋转推导过程

1.基本概念

(1) 四元数的一般形式如下: q=q0+q1i+q2j+q3k q = q 0 + q 1 i + q 2 j + q 3 k
(2) 单位四元数:满足四元数的模为1,即 q02+q12+q22+q32=1 q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1
(3) 四元数的三角形式: q=cosθ2+u⃗ sinθ2 q = c o s θ 2 + u → s i n θ 2
(4)共轭四元数: q∗=q0−q1i−q2j−q3k q ∗ = q 0 − q 1 i − q 2 j − q 3 k
(5) 纯四元数: q=q1i+q2j+q3k q = q 1 i + q 2 j + q 3 k
(6)四元数与空间旋转:

Rq(p)=qpq−1 R q ( p ) = q p q − 1

其中:
q q :单位四元数
q−1 q − 1 :四元数的逆,对于单位四元数, q∗=q−1 q ∗ = q − 1
p p :纯四元数
Rq(p):也是一个纯四元数 R q ( p ) : 也 是 一 个 纯 四 元 数

---

2. 欧拉角的万向锁问题

先看一个简单的欧拉旋转，如下图所示：欧拉旋转需要先确定旋转顺序，我们可以定义X-Y-Z的顺序（总共有12种旋转顺序），那么什么是万向锁呢，我们可以用手机在桌子上进行旋转，以手机的正面为xy平面，以手机的厚度的方向作为z轴，我们先绕x转一个角度，然后再绕y轴旋转90度，我们会发现一个问题，当我们再绕z轴旋转一个角度，效果等同于我开始绕x轴旋转另外一个角度,再绕y轴旋转90度就行了.

我们的欧拉旋转只能表示二维空间了，这是解我们的微分方程会出现退化现象，造成我们的微分方程无法解的情况。这样说似乎还是比较模糊，那么我们举一个例子:

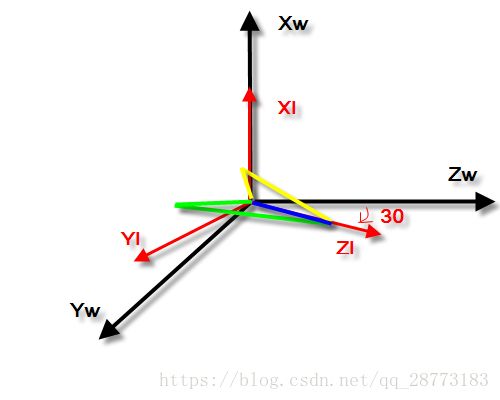
如图所示: XwYwZw X w Y w Z w 是世界坐标系, XiYiZi X i Y i Z i 是机体坐标系,我们先绕 Xi X i 轴旋转 30∘ 30 ∘ ,再绕 Yi Y i 旋转 90∘ 90 ∘ ,如下图所示:

此时我们的 Xw X w 和 Zi Z i 在同一直线上,最后我们再绕 Zi Z i 旋转 40∘ 40 ∘ ,如下图所示:

我们会发现一个问题，无论我们怎么旋转，我们的坐标都是（30,90，z）,也就是绕z轴的旋转角度我们无法衡量的，这也就是我们的万向锁问题。

---

3. 四元数推导

复数旋转

首先我们看一个复数 p=a+bi p = a + b i 在复平面的表示:
现在我们将它旋转角度 θ θ ,先定义另外一个复数 q=cosθ+isinθ q = c o s θ + i s i n θ ,我们发现,复数的乘法表示了一种旋转:

qp=(acosθ−bsinθ)+i(asinθ+bcosθ) q p = ( a c o s θ − b s i n θ ) + i ( a s i n θ + b c o s θ )

这个复数恰好就是 p p 旋转 θ θ 角度后的值:

三维复数旋转

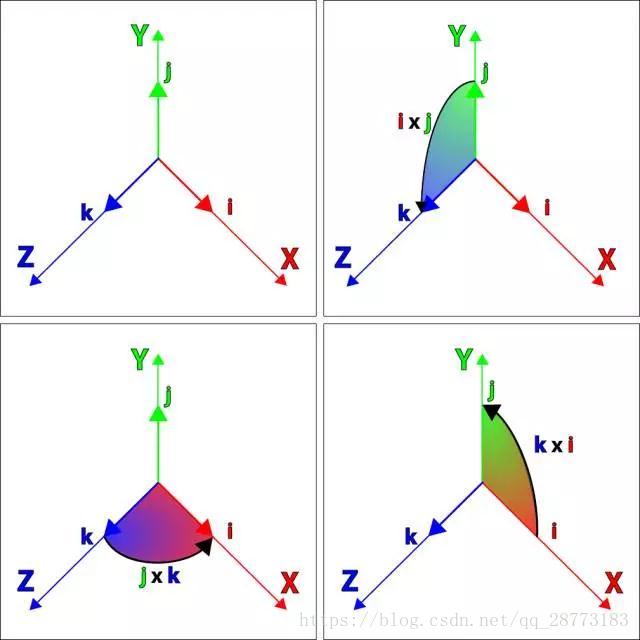
我们看到了二维复数乘法可以表示旋转，那么三维空间呢。按照举一反三的思想，我们会想到再增加一个虚数作为第三个维度，这个就要涉及到我们的向量的叉乘，如下图所示：

向量叉乘的结果是两个向量构成平面的垂直向量,那么我们定义两个个三维的复数:

z1=a1+b1i+c1jz2=a2+b2i+c2j z 1 = a 1 + b 1 i + c 1 j z 2 = a 2 + b 2 i + c 2 j

其中 i2=j2=−1 i 2 = j 2 = − 1 ,我们类似的进行复数的乘法,得到:

z1z2=(a1a2−b1b2−c1c2)+(a1b2+a2b1)i+(a1c2+a2c1)j+b1c2ij+b2c1ji z 1 z 2 = ( a 1 a 2 − b 1 b 2 − c 1 c 2 ) + ( a 1 b 2 + a 2 b 1 ) i + ( a 1 c 2 + a 2 c 1 ) j + b 1 c 2 i j + b 2 c 1 j i

我们会发现,如果没有 ij和ji i j 和 j i 这两项,我们三维的复数旋转也就没问题,那该如何处理呢?

四元数旋转

哈密尔顿引入四维的四元数: q=q0+q1i+q2j+q3k,其中i2=j2=k2=−1 q = q 0 + q 1 i + q 2 j + q 3 k , 其 中 i 2 = j 2 = k 2 = − 1 ,根据向量的叉乘可以定义下列一些关系:




可以得到下列关系:

ij=−ji=kjk=−kj=iki=−ik=ji2=j2=k2=ijk=−1 i j = − j i = k j k = − k j = i k i = − i k = j i 2 = j 2 = k 2 = i j k = − 1

为了方便理解,我们将四元数写成向量的形式: q=[s,v⃗ ] q = [ s , v → ] ,我们可以理解为 s s 为实部,向量 v⃗  v → 表示的就是三维空间,下面我们看一下四元数的乘法:

qa=[sa,a⃗ ]qb=[sb,b⃗ ]qaqb=[sasb−a⃗ ⋅b⃗ ,sab⃗ +sba⃗ +a⃗ ×b⃗ ] q a = [ s a , a → ] q b = [ s b , b → ] q a q b = [ s a s b − a → ⋅ b → , s a b → + s b a → + a → × b → ]

由于我们研究的是三维空间,因此我们可以令 qa q a 为一个纯四元数,即 qa=[0,a⃗ ] q a = [ 0 , a → ] .则可以得到:

qaqb=[−a⃗ ⋅b⃗ ,sba⃗ +a⃗ ×b⃗ ] q a q b = [ − a → ⋅ b → , s b a → + a → × b → ]

从上面可以看到,一个普通的四元数是无法将三维空间映射到三维空间的,我们令向量点乘的部分为零,此时,一个纯四元数就可以旋转为另一个纯四元数.为了表现出旋转,这里我们用四元数的三角表示方式: qb=[cosθ,sinθb⃗ ] q b = [ c o s θ , s i n θ b → ] ,令 a⃗ ⋅b⃗ =0 a → ⋅ b → = 0 ,则有:

qaqb=[0,a⃗ cosθ+a⃗ ×b⃗ sinθ] q a q b = [ 0 , a → c o s θ + a → × b → s i n θ ]

我们没有对向量 b⃗  b → 做任何限制,下面来用一个例子说明应当对向量 b⃗  b → 做什么限制.
令 p=[0,2i],q=[2√2,2√2b⃗ ] p = [ 0 , 2 i ] , q = [ 2 2 , 2 2 b → ] ,考虑到 a⃗ ⋅b⃗ =0 a → ⋅ b → = 0 ,令 b⃗ =|b⃗ |k b → = | b → | k ,则将 p p 旋转 45∘ 45 ∘ 后得到:

p′=qp=[0,2–√|b⃗ |i+2–√|b⃗ |j] p ′ = q p = [ 0 , 2 | b → | i + 2 | b → | j ]

旋转之前,纯四元数 p p 的模长为 |p|=2 | p | = 2 ,旋转过后,纯四元数 p′ p ′ 的模长 |p′|=2|b⃗ | | p ′ | = 2 | b → | ,所以我们要给旋转四元数又加上一个约束:四元数 q q 的模长为1,即 q q 是一个单位四元数.

但是上面的旋转是有缺点的,因为其限制了我们的旋转轴和需要被旋转的四元数必须是垂直的( a⃗ ⋅b⃗ =0 a → ⋅ b → = 0 ),而不能达到任意的旋转.这时,聪明的哈密尔顿发现,一个四元数会把一个纯四元数拉到四维空间,但它的共轭又会把这个四维的空间拉回到三维空间.我们以一个简单的例子来说明这个问题:

p=[0,2i],q=[fracsqrt22,fracsqrt66(i+j+k)],则q∗=[fracsqrt22,−fracsqrt66(i+j+k)] p = [ 0 , 2 i ] , q = [ f r a c s q r t 2 2 , f r a c s q r t 6 6 ( i + j + k ) ] , 则 q ∗ = [ f r a c s q r t 2 2 , − f r a c s q r t 6 6 ( i + j + k ) ]

旋转之后的四元数 Rq(p) R q ( p ) :

Rq(p)=[0,2j] R q ( p ) = [ 0 , 2 j ]

这里需要注意的一点是,因为经过两次的旋转,所以旋转的角度是 2θ 2 θ ,这就是为什么我们常常看到的旋转四元数是一下形式:

q=cosθ2+u⃗ sinθ2,其中|u⃗ |=1 q = c o s θ 2 + u → s i n θ 2 , 其 中 | u → | = 1

---

Quaternions – Ken Shoemake

---

参考资料

1. Understanding Quaternions 中文翻译《理解四元数》
2. 视觉SLAM中的数学基础 第二篇 四元数
3. 四元数与空间旋转 – 维基
4. 四元数 – 维基
5. Shoemake, Quaternions