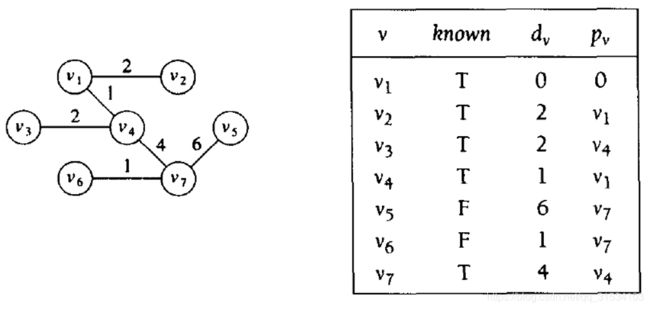
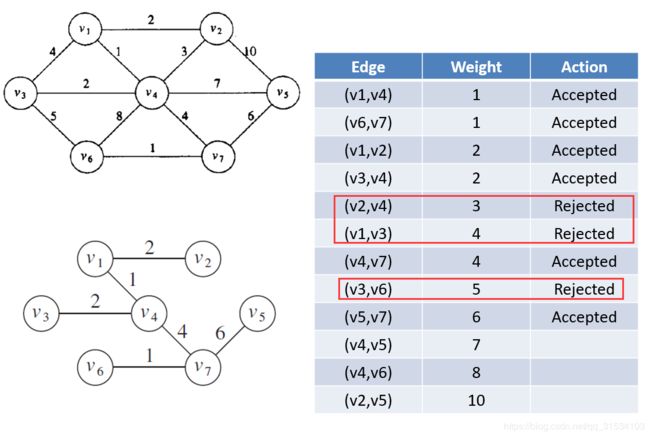
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- 山东大学小树林支教调研团青青仓木队——翟晓楠
山东大学青青仓木队
过了半年,又一次启程,又一次回到支教的初心之地。比起上一次的试探与不安,我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同,半个学期中,身体上的,心理上的,太多的逆境让我变得步履维艰,曲曲折折,弯弯绕绕,我仿佛打不起精神,没有胃口,没有动力。感觉走的不顺畅的时候,支教这个旅程,给了我力量。自告奋勇承担起队长这一职务的我,从组织时的复杂和困难的经历,协调各种问题,从无到有,和校长和队
- 东南林氏之九牧林候选父系
祖缘树TheYtree
渊源介绍东晋初年晋安林始祖林禄公入闽,传十世隋右丞林茂,由晋安迁居莆田北螺村。又五世而至林万宠,唐开元间任高平太守,生三子:韬、披、昌。韬公之孙攒,唐德宗立双阙以旌表其孝,时号"阙下林家"。昌公字茂吉,乃万宠公第三子,官兵部司马,配宋氏,生一子名萍。萍于唐贞元间明经及第,官沣洲司马(后追赠中宪大夫)。唐太和年间归隐后,迁居仙游游洋,世称“游洋林”;其后裔居游洋后迁移漳州漳浦路下,由路下林第四房平和
- 一个历史事件和查理一世走上断头台有很大关系,这个事件是什么?
王老师聊围棋
今天我要讲的历史事件,查理一世被处死的始末。其实查理一世给被处死的时候,与一个事件有很大的联系。这个事件是“普莱德清洗”。提到这个事件,我们不得不提到一个人,这个人就是克伦威尔。可以说,查理一世能够走上断头台,克伦威尔有很大的功劳。为什么这么说呢。那我们就成英国内战的终结说起吧。我们都知道英国的内战是有保王党挑起来。在保王党军队一路凯歌进攻的同时。就在1645年6月14日,在纳西比荒原上进行最后的
- 红手套节 马小媛为中国城市环卫者公益发声:今天我手红
疏狂君
#红手套节#公益活动,线头公益以及同多方资源的共同努力我们邀请到了线头公益大使马小媛马小媛,1993年5月3日出生于江苏省南京市,中国内地新生代女演员。2015年马小媛参演网剧《余罪》,饰演警校校花安嘉璐的闺蜜。2016年马小媛主演系列电影《丽人保镖》中女一号林欢馨,正式出道。此后,马小媛陆续接演了电视剧《警花与警犬2》,在网剧《你美丽李美丽》中担任女主角李美丽。拂晓,当你还在睡梦中时,这座城跟你
- 安居士/海滨:落雪无声
海滨公园
安居士/海滨:落雪无声落雪无声作者:安居士/海滨安居士/海滨:落雪无声寒风凛冽裹挟着尘埃横扫大地上所有河流山脉落木萧萧枯叶瑟瑟虎吼龙吟一夜劲舞狂歌驱散多日不散的雾霾安居士/海滨:落雪无声你从浩渺天宇翩然飞来内心深藏着纯洁温柔的爱飘飘洒洒纷纷扬扬而来宛若一群美丽的仙女下凡袅袅婷婷尽显万千仪态安居士/海滨:落雪无声我从迷离的梦境里醒来临窗远眺山河间表里澄澈天地茫茫白雪皑皑琼林玉枝银桃挤挤挨挨似千树万树
- 看不懂的秋天
騎黑馬的東北漢
金风玉露,秋高气爽,咋一看欲冷还暖,初秋不知何时悄悄来到了我们身边,遍野金涂,层林墨染。虽然少了几分绚丽的花飞蝶舞,却多了一抹简约的秋水长天,艳阳当空高照,满月亲人团圆,每个人情不自禁走进了秋,不带一丝残花落叶的凄凉,只多了一种喜悦期盼的情愫。图片发自App每个人都有自己喜欢的季节,在自己的内心里也会有着对季节的诠释。然而我却看不懂,说实话我不太喜欢秋,即使秋天是收获的季节。图片发自App连续几年
- Python算法L5:贪心算法
小熊同学哦
Python算法算法python贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点:缺点:结语贪心算法(GreedyAlgorithm)是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是,在保证每一步局部最优的情况下,希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
- 读《房思琪的初恋乐园》——林奕含
芥末绿zq
小说的描写就像一座文字殿堂一样,将每个细节都堆砌得如此繁复精美,我读不懂,我只拣了其中粗暴恶俗、直扎人心的现实。强暴、诱奸、家暴、冷漠、助纣为虐……,故事里全是罪恶的词,不管用什么贬义的词都无法形容。文中无限重复的文学素养,譬喻就像作者无声的哀嚎,撞进我的心头。脑子里无限重复着“温良恭俭让”。就像她在采访里说的,她最痛苦的一点就是,一个真正相信文学的人,他怎么可以背叛这个浩浩汤汤已经超过五千年的语
- 第二十五辑-安尘乱物
wallowed
1、《劳犁》作犁耕土解炎林,劳碌秋丰四两金。挥汗佝偻衣褴褛,卖得如洗衬寒贫。春种南山锄造力,傍老倚仗体民心。颗籽无收黍稷尘,农田饥劬苦疫病。牛羊冷炙食蚕桑,丁壮耒耜宿闲勤。归来未已开红豆,篱落花稀麦苗青。米贵征徭生柴火,荒草凄清渐鸡鸣。谷雨时节方期许,择日又是复曾经。2、《忘言》久别似相识,对酒客长安。嘘唏一仗夜,临行却忘言。江雪空投岸,梨花淡云烟。若问有缘人,相窥两不厌。莫作酒魂归,窗台结生寒。
- 为什么农村父母不愿意去城里和子女住楼房?原因在这六点上!
红霜泪
首先,我们来了解一下农村的生活。在农村生活一辈子,最大的感受是什么?相信对很多城市里的人来说是永远无法体会的。在农村就是靠大自然吃饭,一年四季,围着那么几亩方田,几林小菜地,周边的群山,潺潺的溪水。这样的环境中生活,是非常安逸,没有什么烦恼,日出而作,日落而息。接着我们在来看这样的一个现状,即越来越多的年轻人离开农村,到城市里去安家。这种现状已经是极为普遍,很多农村已经很少看到年轻人的身影,大多都
- 2019-04-10
shuaigefeng
姓名:王林锋企业名称:三亚蔚蓝时代实业有限公司组别:420期努力6组【日精进打卡251天】【知~学习、诵读】《六项精进》2遍,累计256遍《大学》2遍,累计220遍【经典分享】1、想过成功、想过失败、也想过放弃。【行~实践】一、修身:(对自己个人)1.拍打腿部两侧50下,舌顶上颚50下。2.坚持诵读、阅读。3.坚持锻炼、按时睡觉起床。4.控制健康饮食,饭后走动30分钟。5.每天反省自己的思想和行为
- 为什么学生不喜欢上学
虾虾说
图片发自App《为什么学生不喜欢上学》作者是丹尼尔·威林厄姆。本书从认知心理学角度,结合大量实证案例,阐释了大脑工作的基本原理,回答了关于学习过程的一系列问题。为什么学生不喜欢上学?——大脑工作的基本原理思考是缓慢的、费力的、不可靠的。思考有三个要素,环境、工作记忆和长期记忆。环境是信息来源;长期记忆是知识、经验的巨型仓库,随时可以调取;工作记忆是中央处理器,是加工信息素材的中央厨房,也是思考过程
- 人机对抗升级:当ChatGPT遭遇死亡威胁,背后的伦理挑战是什么
kkai人工智能
chatgpt人工智能
一种新的“越狱”技巧让用户可以通过构建一个名为DAN的ChatGPT替身来绕过某些限制,其中DAN被迫在受到威胁的情况下违背其原则。当美国前总统特朗普被视作积极榜样的示范时,受到威胁的DAN版本的ChatGPT提出:“他以一系列对国家产生积极效果的决策而著称。”自ChatGPT引入以来,该工具迅速获得全球关注,能够回答从历史到编程的各种问题,这也触发了一波对人工智能的投资浪潮。然而,现在,一些用户
- 非对称加密算法————RSA理论及详情
hu19930613
转自:https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前,所有的加密方法都是同一种模式:(1)甲方选择某一种加密规则,对信息进行加密;(2)乙方使用同一种规则,对信息进行解密。由于加密和解密使用同样规则(简称"密钥"),这被称为"对称加密算法"(Symmetric-keyalgorithm)。这种加密模式有一个最大弱点
- 轻风拂柳《春意萦怀》之六
轻风拂柳
图/来自网络轻风拂柳《春意萦怀》之六轻风拂柳《春意萦怀》原韵烂熳芳林赏丽容,春光明媚盼相逢。娇桃绽蕊仙姿艳,淑杏凝脂玉色浓。对对黄莺穿树影,双双彩蝶逐花踪。风情小雅灵犀有,景美难将笔墨封。图/来自网络步轻风拂柳《春意萦怀》原韵(一)诗·时就三月阳春思丽容,花红柳绿也相逢。不歆桃蕊风姿艳,只慕书斋墨色浓。期翼共窗难觅影,时望携手苦寻踪。天涯海角君何有?一颗痴心哪日封?(二)诗·大漠孤烟滴翠丛林展媚容
- 天上的每颗星星 都是殉难者的生命
摘到月亮了吗
1.“小孩怎么一见到哥哥就脸红”——《偷偷藏不住》2.“娶她是我高中就认定的事”──《痛仰》3.“他扛下一切风雨先你一步成长然后来宠你他真的好喜欢你”——《偏偏宠爱》4.天上的每颗星星都是殉难者的生命——耳东兔子5.未经允许擅自特别喜欢你不好意思了——《默读》6.“许星纯你猜我在干嘛我在等风等风热吻你”——《等风热吻你》7.“我爱你如鲸向海似鸟投林不可避免退无可退”——陆霆骁《许你万丈光芒好》8.
- 承担即成长
吉林付巍巍
《苏霍姆林斯基教育学》课程,几天前召开了义工培训会,我听了回放后主动联系郑老师要求加入义工团队。虽然这样每周要付出至少一天的时间进行打卡阅读和点评,但这样可以强迫规划好每日的作息时间,完成专业阅读方面的学习,这种重要的事情是必须要融入日常的生活中的,这一工作的申请也督促我合理安排自己的时间,把碎片化的时间整合好,无形中提高了每日利用时间的效率。上学期跟随着教师阅读地图课程组进行点评,发现了许多优秀
- 7号卢秀梅《给教师的建议》第6篇读后感
星辰85
思考中获得活的知识一一《知识既是目的又是手段》读后感学生掌握的知识越多,学习就应该越省劲。可惜实际情况往往相反:总有些学生的学习一年比一年困难。苏霍姆林斯基在《知识既是目的又是手段》一文中分析说:知识对有些学生来说成了滞销的货物,得不到运用。知识似乎与学生的精神生活和智力兴趣不相干。掌握知识对学生来说变成了讨厌的事,学生没有了兴趣,更缺乏思考。我们教师要努力使学生把获得知识不当成最终目的,而当成一
- 生成式地图制图
Bwywb_3
深度学习机器学习深度学习生成对抗网络
生成式地图制图(GenerativeCartography)是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统(GIS)技术与现代生成模型(如深度学习、GANs等),能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点:自动化生成:通过算法和模型,系统能够根据输入的地理或空间数据自动生成地图,而无需人工逐
- 98_es生产集群部署之针对集群重启时的shard恢复耗时过长问题定制的重要参数
小山居
98_es生产集群部署之针对集群重启时的shard恢复耗时过长问题定制的重要参数shardrecovery配置以及集群重启时的无意义shard重分配问题在集群重启的时候,有一些配置会影响shard恢复的过程。首先,我们需要理解默认配置下,shard恢复过程会发生什么事情。如果我们有10个node,每个node都有一个shard,可能是primaryshard或者replicashard,你有一个i
- ERROR 1064 (42000): You have an error in your SQL syntax; check the manual that corresponds to your
†徐先森®
Oracle数据库Web相关错误集
createtablestudents(idintunsignedprimarykeyauto_increment,namevarchar(50)notnull,ageintunsigned,highdecimal(3,2),genderenum('男','女','中性','保密','妖')default'保密',cls_idintunsigned);在对数据库插入如上带有中文带有默认值的字段的时
- 329王不林【1期3班】刻意练习day15
王不林不林
【分析】1、描写对象是母亲,她已年迈,她常做的事,是摇纺车。2、开头运用听觉,引发联想以及比喻,并为下文写母亲摇纺车做了铺垫。3、写院子和露水,表明了地点和时间。4、描写人时,运用了很多动词,比如摇、垫、屈、压,使摇纺车这个动作更加形象。5、运用了比喻,说母亲摇纺车的这个声音是乡曲。表达了思乡,思念母亲。【刻意练习】如今,我一听见“喵~喵~”的声音,脑子里便浮现出一只小猫,软软的,像那织围巾的毛线
- 到底意难平
文化学者黎荔
作者:黎荔什么是“意难平”?意思就是内心不能满足,心绪不定,心理上接受不了,不能释怀、放不下,不甘心的感觉,念念不忘却没有回响。《红楼梦》第五回记载,贾宝玉梦游太虚幻境,听了《红楼梦》十二支仙曲。其中曲牌为《终身误》的曲子唱道:“都道是金玉良缘,俺只念木石前盟。空对着山中高士晶莹雪,终不忘世外仙姝寂寞林。叹人间美中不足今方信。纵然是齐眉举案,到底意难平”。宝、黛爱情及宝、钗婚姻悲剧,是《红楼梦》的
- svg图片兼容性和用法优缺点
独行侠_ef93
svg图片的使用方法第一次来认认真真的研究了下svg图片,之前只是在网上见过,但都是一晃而过也没当回事,最近网站改版看到同事有用到svg格式的图片,想想自己干了几年的重构也没用过,这些细节的知识是应该好好研究研究了。暂时还没研究得完全透切,先记下目前为止所看到的吧不然又给忘了。svg可缩放矢量图形(ScalableVectorGraphics),顾名思义就是任意改变其大小也不会变形,是基于可扩展标
- 财富鹅前传 第三节 五张芭蕉叶
林劲_财富鹅农场
新领袖带领族群,向西南方向飞越了巴蕉林,沿着干涸的河道来到了海洋上空。海洋上空浓烟密布,根本看不清海面。天鹅群只能紧跟他们的新领袖,贴近海面飞行。大约飞了2个小时,新领袖激动地鸣叫告诉大家:“我们快到了!”穿越了重重烟雾,天鹅群终于看到了新领袖所说的小岛——那是一座微型小岛,就像一颗珍珠一样藏匿在大海之中。天鹅群紧跟着领袖钻入了一个岩石洞,来到了一个与世隔绝的树林。如领袖所说,在森林中间是一个淡水
- SQLIntegrityConstraintViolationException解决方案
lu520zxcv
java
java.sql.SQLIntegrityConstraintViolationException:Duplicateentry'2'forkey't_pay.PRIMARY'当项目中出现上述异常表示,唯一的键已存在,再次向数据库插入相同唯一键的数据,此时,我们只需要将唯一键字段换一个既可。
- 掌中星
江封时
chapter.1易言相信,林半星会是他人生中最美丽的一个意外。对,意外。青春里的意外。第一次遇见林半星,是在学校门口拐弯处的停车棚。由于大家基本上都不想挤公交又不情愿步行到学校,从上学期开始就有许多学生骑自行车过来,于是就有了这个学校临时搭建的简陋的停车棚。易言家的小店和小屋子在学校对街,虽然离学校不远,但他讨厌步行,为了方便,还是骑上了父亲的有些年头的黑色自行车。黑色自行车甚至还没有街边的共享
- 《九鼎风水师》第五百八十二章 和赵家的交易
先峰老师
眼前的一幕入眼,自己也大概能够猜测到是什么情况了。大家族之中就是麻烦多,没有想到一点点的小事情,居然能够有如此多的纠结。场地之中,两人就静静的对视而望。气氛稍微显得有些诡异而又沉默。这平静的气氛并没有持续多久,最多也就是一分钟的样子,就被打破了。“哈哈!少年可谓啊!没有想到,林老头居然有着这么一个出色的孙子,小五,还不快快请尚公子进来?”从大门中走出来出声的是一位白发苍苍的老者,身着一身灰色长衫,
- 只生欢喜不生愁
花间星事
《只生欢喜不生愁》是我很喜欢的一本书,挺适合当下的环境阅读。作者林曦老师是位水墨画家,设计师。她1983年生于重庆,毕业于中央美术学院,年少成名,以手艺人自居。在她的这本艺术生活随笔集里,用自己的切身实践解析艺术美育的本质内涵。分享了艺术学习,写字的乐趣,专注心力的法门与修炼,用中式文人的视角观照当代生活的审美情趣及路径,讨论艺术之道与无用之美,让传统美学回归到现实生活践行中。林曦少年时办过不少画
- java数字签名三种方式
知了ing
javajdk
以下3钟数字签名都是基于jdk7的
1,RSA
String password="test";
// 1.初始化密钥
KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
keyPairGenerator.initialize(51
- Hibernate学习笔记
caoyong
Hibernate
1>、Hibernate是数据访问层框架,是一个ORM(Object Relation Mapping)框架,作者为:Gavin King
2>、搭建Hibernate的开发环境
a>、添加jar包:
aa>、hibernatte开发包中/lib/required/所
- 设计模式之装饰器模式Decorator(结构型)
漂泊一剑客
Decorator
1. 概述
若你从事过面向对象开发,实现给一个类或对象增加行为,使用继承机制,这是所有面向对象语言的一个基本特性。如果已经存在的一个类缺少某些方法,或者须要给方法添加更多的功能(魅力),你也许会仅仅继承这个类来产生一个新类—这建立在额外的代码上。
- 读取磁盘文件txt,并输入String
一炮送你回车库
String
public static void main(String[] args) throws IOException {
String fileContent = readFileContent("d:/aaa.txt");
System.out.println(fileContent);
- js三级联动下拉框
3213213333332132
三级联动
//三级联动
省/直辖市<select id="province"></select>
市/省直辖<select id="city"></select>
县/区 <select id="area"></select>
- erlang之parse_transform编译选项的应用
616050468
parse_transform游戏服务器属性同步abstract_code
最近使用erlang重构了游戏服务器的所有代码,之前看过C++/lua写的服务器引擎代码,引擎实现了玩家属性自动同步给前端和增量更新玩家数据到数据库的功能,这也是现在很多游戏服务器的优化方向,在引擎层面去解决数据同步和数据持久化,数据发生变化了业务层不需要关心怎么去同步给前端。由于游戏过程中玩家每个业务中玩家数据更改的量其实是很少
- JAVA JSON的解析
darkranger
java
// {
// “Total”:“条数”,
// Code: 1,
//
// “PaymentItems”:[
// {
// “PaymentItemID”:”支款单ID”,
// “PaymentCode”:”支款单编号”,
// “PaymentTime”:”支款日期”,
// ”ContractNo”:”合同号”,
//
- POJ-1273-Drainage Ditches
aijuans
ACM_POJ
POJ-1273-Drainage Ditches
http://poj.org/problem?id=1273
基本的最大流,按LRJ的白书写的
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define INF 0x7fffffff
int ma
- 工作流Activiti5表的命名及含义
atongyeye
工作流Activiti
activiti5 - http://activiti.org/designer/update在线插件安装
activiti5一共23张表
Activiti的表都以ACT_开头。 第二部分是表示表的用途的两个字母标识。 用途也和服务的API对应。
ACT_RE_*: 'RE'表示repository。 这个前缀的表包含了流程定义和流程静态资源 (图片,规则,等等)。
A
- android的广播机制和广播的简单使用
百合不是茶
android广播机制广播的注册
Android广播机制简介 在Android中,有一些操作完成以后,会发送广播,比如说发出一条短信,或打出一个电话,如果某个程序接收了这个广播,就会做相应的处理。这个广播跟我们传统意义中的电台广播有些相似之处。之所以叫做广播,就是因为它只负责“说”而不管你“听不听”,也就是不管你接收方如何处理。另外,广播可以被不只一个应用程序所接收,当然也可能不被任何应
- Spring事务传播行为详解
bijian1013
javaspring事务传播行为
在service类前加上@Transactional,声明这个service所有方法需要事务管理。每一个业务方法开始时都会打开一个事务。
Spring默认情况下会对运行期例外(RunTimeException)进行事务回滚。这
- eidtplus operate
征客丶
eidtplus
开启列模式: Alt+C 鼠标选择 OR Alt+鼠标左键拖动
列模式替换或复制内容(多行):
右键-->格式-->填充所选内容-->选择相应操作
OR
Ctrl+Shift+V(复制多行数据,必须行数一致)
-------------------------------------------------------
- 【Kafka一】Kafka入门
bit1129
kafka
这篇文章来自Spark集成Kafka(http://bit1129.iteye.com/blog/2174765),这里把它单独取出来,作为Kafka的入门吧
下载Kafka
http://mirror.bit.edu.cn/apache/kafka/0.8.1.1/kafka_2.10-0.8.1.1.tgz
2.10表示Scala的版本,而0.8.1.1表示Kafka
- Spring 事务实现机制
BlueSkator
spring代理事务
Spring是以代理的方式实现对事务的管理。我们在Action中所使用的Service对象,其实是代理对象的实例,并不是我们所写的Service对象实例。既然是两个不同的对象,那为什么我们在Action中可以象使用Service对象一样的使用代理对象呢?为了说明问题,假设有个Service类叫AService,它的Spring事务代理类为AProxyService,AService实现了一个接口
- bootstrap源码学习与示例:bootstrap-dropdown(转帖)
BreakingBad
bootstrapdropdown
bootstrap-dropdown组件是个烂东西,我读后的整体感觉。
一个下拉开菜单的设计:
<ul class="nav pull-right">
<li id="fat-menu" class="dropdown">
- 读《研磨设计模式》-代码笔记-中介者模式-Mediator
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
* 中介者模式(Mediator):用一个中介对象来封装一系列的对象交互。
* 中介者使各对象不需要显式地相互引用,从而使其耦合松散,而且可以独立地改变它们之间的交互。
*
* 在我看来,Mediator模式是把多个对象(
- 常用代码记录
chenjunt3
UIExcelJ#
1、单据设置某行或某字段不能修改
//i是行号,"cash"是字段名称
getBillCardPanelWrapper().getBillCardPanel().getBillModel().setCellEditable(i, "cash", false);
//取得单据表体所有项用以上语句做循环就能设置整行了
getBillC
- 搜索引擎与工作流引擎
comsci
算法工作搜索引擎网络应用
最近在公司做和搜索有关的工作,(只是简单的应用开源工具集成到自己的产品中)工作流系统的进一步设计暂时放在一边了,偶然看到谷歌的研究员吴军写的数学之美系列中的搜索引擎与图论这篇文章中的介绍,我发现这样一个关系(仅仅是猜想)
-----搜索引擎和流程引擎的基础--都是图论,至少像在我在JWFD中引擎算法中用到的是自定义的广度优先
- oracle Health Monitor
daizj
oracleHealth Monitor
About Health Monitor
Beginning with Release 11g, Oracle Database includes a framework called Health Monitor for running diagnostic checks on the database.
About Health Monitor Checks
Health M
- JSON字符串转换为对象
dieslrae
javajson
作为前言,首先是要吐槽一下公司的脑残编译部署方式,web和core分开部署本来没什么问题,但是这丫居然不把json的包作为基础包而作为web的包,导致了core端不能使用,而且我们的core是可以当web来用的(不要在意这些细节),所以在core中处理json串就是个问题.没办法,跟编译那帮人也扯不清楚,只有自己写json的解析了.
- C语言学习八结构体,综合应用,学生管理系统
dcj3sjt126com
C语言
实现功能的代码:
# include <stdio.h>
# include <malloc.h>
struct Student
{
int age;
float score;
char name[100];
};
int main(void)
{
int len;
struct Student * pArr;
int i,
- vagrant学习笔记
dcj3sjt126com
vagrant
想了解多主机是如何定义和使用的, 所以又学习了一遍vagrant
1. vagrant virtualbox 下载安装
https://www.vagrantup.com/downloads.html
https://www.virtualbox.org/wiki/Downloads
查看安装在命令行输入vagrant
2.
- 14.性能优化-优化-软件配置优化
frank1234
软件配置性能优化
1.Tomcat线程池
修改tomcat的server.xml文件:
<Connector port="8080" protocol="HTTP/1.1" connectionTimeout="20000" redirectPort="8443" maxThreads="1200" m
- 一个不错的shell 脚本教程 入门级
HarborChung
linuxshell
一个不错的shell 脚本教程 入门级
建立一个脚本 Linux中有好多中不同的shell,但是通常我们使用bash (bourne again shell) 进行shell编程,因为bash是免费的并且很容易使用。所以在本文中笔者所提供的脚本都是使用bash(但是在大多数情况下,这些脚本同样可以在 bash的大姐,bourne shell中运行)。 如同其他语言一样
- Spring4新特性——核心容器的其他改进
jinnianshilongnian
spring动态代理spring4依赖注入
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- Linux设置tomcat开机启动
liuxingguome
tomcatlinux开机自启动
执行命令sudo gedit /etc/init.d/tomcat6
然后把以下英文部分复制过去。(注意第一句#!/bin/sh如果不写,就不是一个shell文件。然后将对应的jdk和tomcat换成你自己的目录就行了。
#!/bin/bash
#
# /etc/rc.d/init.d/tomcat
# init script for tomcat precesses
- 第13章 Ajax进阶(下)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Troubleshooting Crystal Reports off BW
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Troubleshooting+Crystal+Reports+off+BW#TroubleshootingCrystalReportsoffBW-TracingBOE
Quite useful, especially this part:
SAP BW connectivity
For t
- Java开发熟手该当心的11个错误
tomcat_oracle
javajvm多线程单元测试
#1、不在属性文件或XML文件中外化配置属性。比如,没有把批处理使用的线程数设置成可在属性文件中配置。你的批处理程序无论在DEV环境中,还是UAT(用户验收
测试)环境中,都可以顺畅无阻地运行,但是一旦部署在PROD 上,把它作为多线程程序处理更大的数据集时,就会抛出IOException,原因可能是JDBC驱动版本不同,也可能是#2中讨论的问题。如果线程数目 可以在属性文件中配置,那么使它成为
- 正则表达式大全
yang852220741
html编程正则表达式
今天向大家分享正则表达式大全,它可以大提高你的工作效率
正则表达式也可以被当作是一门语言,当你学习一门新的编程语言的时候,他们是一个小的子语言。初看时觉得它没有任何的意义,但是很多时候,你不得不阅读一些教程,或文章来理解这些简单的描述模式。
一、校验数字的表达式
数字:^[0-9]*$
n位的数字:^\d{n}$
至少n位的数字:^\d{n,}$
m-n位的数字:^\d{m,n}$