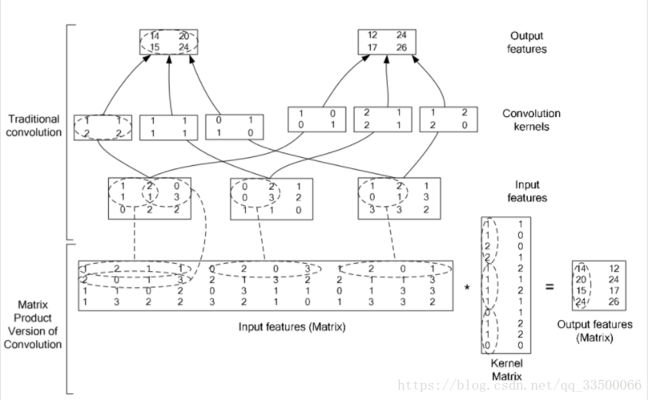
手动实现卷积操作
参考博客https://buptldy.github.io/2016/10/01/2016-10-01-im2col/
# -*- coding:utf8 -*-
import numpy as np
import time
import timeit
#手动实现卷积操作 假设输入图片,核均为正方形,通道数为1,核数量为3,步幅为1,填充为0
X = np.array([[1,2,0],[1,1,3],[0,2,2]])
K = np.array([[[1,1,],[2,2]],[[1,1],[1,1]],[[0,1],[1,0]]])
number =3
kernel_size = 2
# 普通卷积,对应项相乘再求和
def conv_op(bottom,b_size,kernel,kernel_size,number,stride,padding):
top_size = (b_size + 2*padding - kernel_size)/stride+1
top = np.zeros(shape=(number,top_size,top_size))
for c in range(number):#第c个核
for h in range(top_size):#竖直方向第h次截取图的部分
for w in range(top_size):#水平方向第w次
# 先滑动窗口取部分图 依次乘第c个kernel并求和 赋给特征图对应位置
top[c,h,w] = np.sum(bottom[h*stride:h*stride+kernel_size,w*stride:w*stride+kernel_size]*kernel[c])
print top
return top
time1 = time.clock()
conv_op(X,3,K,kernel_size,number,1,0)
time2 = time.clock()
print 'ordinary convOp time:',time2-time1这是简单的方法,将图片和核转化为矩阵,进行点积运算。
这里图片是3通道3X3的,卷积核有2个,通道数为3,尺寸为2,步幅为1,无填充。
#另一种简便的方法把卷积操作变成两个大矩阵的点积
#将输出图变成一个矩阵 每一行表示一个待卷积的部分图拉伸后的结果
def conv_op2(bottom,b_size,kernel_size,stride,padding):
top_size = (b_size + 2*padding - kernel_size)/stride+1 #单维度上应该滑动的次数 即特征图的尺寸
top = np.zeros(shape=(top_size*top_size,kernel_size*kernel_size))
for h in range(top_size):#竖直方向第h次
for w in range(top_size):#水平方向第w次
#print bottom[h*stride:h*stride+kernel_size,w*stride:w*stride+kernel_size]
t=bottom[h*stride:h*stride+kernel_size,w*stride:w*stride+kernel_size]
top[h*top_size+w]=t.reshape(1,4)
return top
time3 = time.clock()
X = conv_op2(X,3,kernel_size,1,0)
time4 = time.clock()
print 'simple convOp time:',time4-time3
# 转化核为一个矩阵
Z=np.zeros(shape=(kernel_size*kernel_size,number))
for i in range(number):
#将第i个核拉伸成(kernel_size*kernel_size,1)形状 并放入Z的第i+1列
Z[:,i:i+1] = K[i].reshape(4,1)
#K = np.reshape(K,()
# 点乘
Q=np.dot(X,Z)
print Q.T.reshape(3,2,2) #还原成特征图
#输出运行时间能看出 后者比前者快了10倍