动态规划——最短路径

题目：

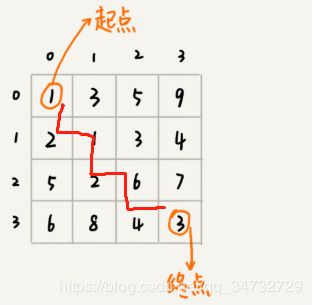
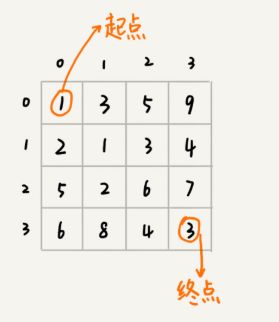
有一个n*n的矩阵WW[n][n]，存储正整数   int WW[4][4] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3}; ，棋子从左上角出发，到右下角，求经过的最短路径。矩阵中每个数值代表距离的长度。

 分析：从[0][0]到[n-1][n-1]，每个阶段都有两种决策，向下或向右。

1. 贪心算法

一条路走到黑，只选择下一步中较小值。

#define N 4
int minDistGreedy(int w[N][N])
{
	int result = w[0][0];
	int i = 0, j = 0;
	while(i < N && j < N)
	{
		if(w[i+1][j] < w[i][j+1])	    // 向下
		{
			result += w[i+1][j];
			++i;
			if (i == N-1 && j < N-1)	// 向下走完，但右边没走完
			{
				while(j < N-1)
				{
					result += w[i][j+1];
					++j;
				}
				break;
			}
		}
		else
		{
			result += w[i][j+1];	    // 向右
			++j;
			if (j == N-1 && i < N-1)	// 向右走完，但下边没走完
			{
				while(i < N-1)
				{
					result += w[i+1][j];
					++i;
				}
				break;
			}
		}
	}
	return result;
}
int main()
{
    int WW[4][4] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3};
    cout << "贪心算法求的最短距离：" << minDistGreedy(WW) << endl;    // 19
    system("pause");
    return 0;
}

2. 回溯算法

总共要走2*（n-1）步

#define N 4
int minDist = 65535;
void minDistBT(int i, int j, int dist, int w[4][4], int n)
{
	if (i == n-1 && j == n-1)
	{
		if (dist+w[i][j] < minDist)    // 此处对最后一个数，进行了特殊处理。因为递归没有处理到
		{
			minDist = dist+w[i][j];
		}
		return;
	}
	if (i < n)
	{
		minDistBT(i+1, j, dist+w[i][j], w, n);
	}
	if(j < n)
	{
		minDistBT(i, j+1, dist+w[i][j], w, n);
	}
}

int main()
{
	int WW[4][4] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3}; 
	minDistBT(0,0,0,WW,4);
	cout << minDist << endl;    // 输出19
	system("pause");
	return 0;
}

关于重复计算的步数，可以通过添加【备忘录】的方式，省去递归。即已经算过的，就不用再计算了。

 3. 动态规划

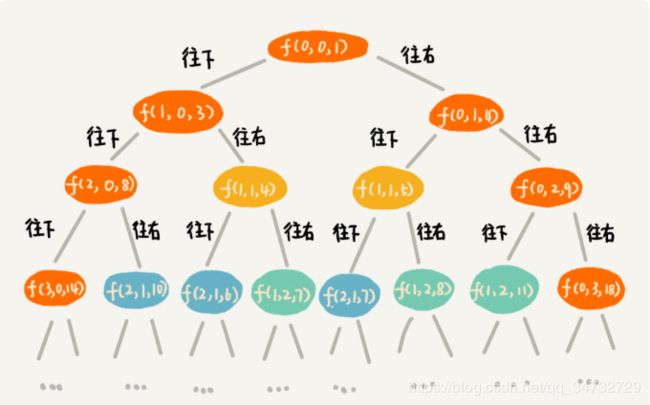
f(i,j,dist);  // i,j 表示位置，dist 表示当前所走的路径长度。 

 

找到公式：min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))   最短路径等于当前值加上左边或上边的较小值。

有了回溯代码之后，画出递归树，找到重复子问题，即重复走过的位置(i,j)相等，但距离不等，取最小。

   

#define N 4
int minDistDP(int w[4][4])
{
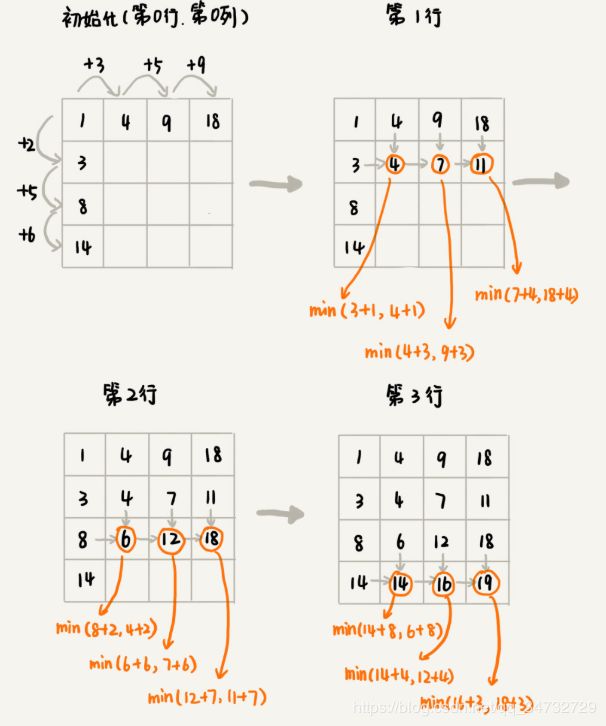
	int states[N][N] = {0};
	int sum = 0;
	for (int j = 0; j < N; ++j)		// 初始化states的第一行数据
	{
		sum += w[0][j];
		states[0][j]=sum;
	}
	sum = 0;
	for (int i = 0; i < N; ++i)		// 初始化states的第一列数据
	{
		sum += w[i][0];
		states[i][0] = sum;
	}
	for (int i = 1; i < N; ++i)
	{
		for (int j = 1; j < N; ++j)
		{
			states[i][j] = w[i][j]+min(states[i-1][j], states[i][j-1]);
		}
	}
	return states[N-1][N-1];
}
int main()
{
    int WW[4][4] = {1,3,5,9,2,1,3,4,5,2,6,7,6,8,4,3};
    cout << "最短距离为：" << minDistDP(WW) << endl;    // 19
    system("pause");
    return 0;
}