Coursera机器学习基石笔记week11

Linear Models for Classification

严谨一点来说，PLA并不是一种“模型”，PLA (Perceptron Learning Algorithm) 是一种“算法”，用来寻找在“线性可分”的情况下，能够把两个类别完全区分开来的一条直线，所以我们简单的把PLA对应的那个模型就叫做Linear Classification。

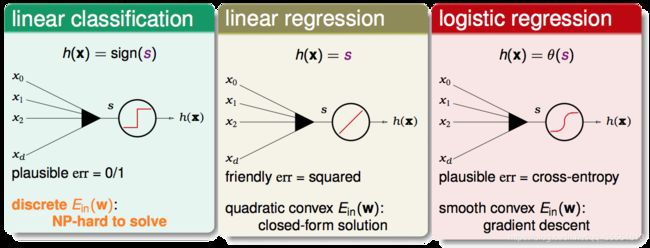
• Linear Classification模型：取s的符号作为结果输出，使用0/1 error作为误差衡量方式，但它的cost function，也就是$E_{in}(w)$是一个离散的方程，并且该方程的最优化是一个NP-hard问题。
• Linear Regression模型：可直接计算出结果，使用平方误差作为误差衡量方式，好处是其$E_{in}(w)$是一个凸二次曲线，非常方便求最优解（可通过矩阵运算一次得到结果）。
• Logistic Regression模型：输出的方程是经过sigmoid的结果，使用cross-entropy作为误差衡量方式，其$E_{in}(w)$是一个凸函数，可以使用gradient descent的方式求最佳解。

Linear Regression和Logistic Regression的输出是一个实数，而不是一个Binary的值，他们能用来解分类问题吗？可以，只要定一个阈值，高于阈值的输出+1，低于阈值的输出-1就好。既然Linear Regression和Logistic Regression都可以用来解分类问题，并且在最优化上，他们都比Linear Classification简单许多，我们能否使用这两个模型取代Linear Classification呢？

这里y是一个binary的值，要么是-1，要么是+1。注意到三个模型的error function都有一个ys的部分，也叫做分类正确性分数 (classification correctness score)。其中s是模型对某个样本给出的分数，y是该样本的真实值。

不难看出，当y=+1时，我们希望s越大越好，当y=−1时，我们希望s越小越好，所以总的来说，我们希望ys尽可能大。因此这里希望给较小的ys较大的cost，给较大的ys较小的cost即可。因此，不同模型的本质差异，就在于这个cost该怎么给。

既然这三个error function都与ys有关，我们可以以ys为横坐标，err为纵坐标，把这三个函数画出来。

从上图可以看出$er{r}_{0/1}$呈阶梯状，ys>0，取0，小于0，取1.而$er{r}_{SQR}$则呈抛物线状，在ys=1左右小范围与$er{r}_{0/1}$相似。而$er{r}_{CE}$是单调递减函数，但是我们发现$er{r}_{CE}$不总是大于$er{r}_{0/1}$，为了方便起见，利用换底公式（${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$）将$er{r}_{CE}$缩放得到$er{r}_{SCE}={\log }_2(1+exp(-ys))=\frac{1}{\ln 2}er{r}_{CE}$，使之一直在$er{r}_{0/1}$之上。

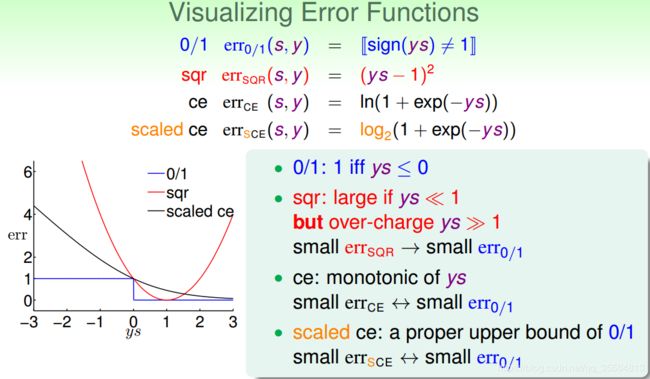
由上图可得：

其实线性回归也可以是线性分类的一个上限，只不过随着ys离1的距离越大，产生的差距越大。但是总的来说线性回归和逻辑回归都可以用来解决linear classification的问题。

下图列举了PLA、linear regression、logistic regression模型用来解linear classification问题的优点和缺点。通常，我们使用linear regression来获得初始化的$w_0$，再用logistic regression模型进行最优化解。

Stochastic Gradient Descent

我们知道PLA与logistic regression都是通过迭代的方式来实现最优化的，即：
$fort=0,1,...w_{t+1}\leftarrow w_t+\eta v$ when stop,return last w as g

区别在于，PLA每次迭代只需要针对一个点进行错误修正，而logistic regression每一次迭代都需要计算每一个点对于梯度的贡献，再把他们平均起来：

这样一来，数据量大的时候，由于需要计算每一个点，那么logistic regression就会很慢了。

​ $w_{t+1}\leftarrow w_t+\eta \frac{1}{N}{\sum }_{n=1}^N\theta (-y_n{w}_t^T{x}_n)(y_n{x}_n)$

那么我们因此可以每次只看一个点，即不要公式中先求和再取平均数的那个部分。随机选择一个点n，它对梯度的贡献为：${\nabla }_{w}err(w,x_n,y_n)$这个可以称之为随机梯度（stochastic gradient）。而真实的梯度，可以认为是随机抽出一个点的梯度值的期望。

因此我们可以把随机梯度当成是在真实梯度上增加一个均值为0的noise：
$stochasticgradient=truegradient+zero-mea{n}^{\prime }nois{e}^{\prime }directions$
单次迭代看，好像会对每一步找到正确梯度方向有影响，但是整体期望值上看，与真实梯度的方向没有差太多，同样能找到最小值位置。随机梯度下降的优点是减少计算量，提高运算速度，而且便于online学习；缺点是不够稳定，每次迭代并不能保证按照正确的方向前进，而且达到最小值需要迭代的次数比梯度下降算法一般要多。

除此之外，还有两点需要说明：1、SGD的终止迭代条件。没有统一的终止条件，一般让迭代次数足够多；2、学习速率η。η的取值是根据实际情况来定的，一般取值0.1就可以了。

Multiclass via Logistic Regression

我们现在已经有办法使用线性分类器解决二元分类问题，但有的时候，我们需要对多个类别进行分类，即模型的输出不再是0和1两种，而会是多个不同的类别。那么如何套用二元分类的方法来解决多类别分类的问题呢？

利用二元分类器来解决多类别分类问题主要有两种策略，OVA(One vs. ALL)和OVO(One vs. One)。

先来看看OVA，假设原问题有四个类别，那么每次我把其中一个类别当成圈圈，其他所有类别当成叉叉，建立二元分类器，循环下去，最终我们会得到4个分类器。

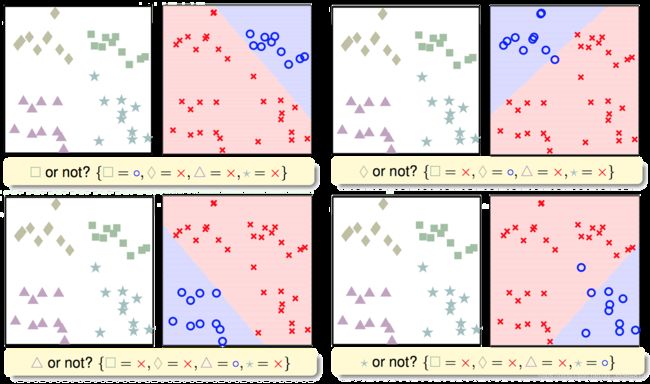
但是这样分类可能会带来一些问题，我们可能会遇到一些边界都不属于上述四类的情况，或者出现某些边界出现都被判断属于多个类的情况，那么这时候使用简单的binary classification就不能很好的解决问题了。

因此我们考虑使用soft软性分类，使用logistic regression来计算某类的概率，通过比较概率来分类。

对于OVA来说，优点就是简单高效，可以使用任何logistic regression类的模型来进行解决。缺点就是如果数据类别太多了，比如100种类别，99种类别做叉叉，1种类别做圈圈，导致两种类别不平衡，因此略微随意的切也能切出较高的准确率，那么就可能会影响分类的效果。

Multiclass via Binary Classfication

所以为了解决这种不平衡问题，我们可以使用OVO策略，即每次只拿两个类别的数据出来建立分类器，如图：

这种方法的优点是更加高效，因为虽然需要进行的分类次数增加了，但是每次只需要进行两个类别的比较，也就是说单次分类的数量减少了。而且一般不会出现数据unbalanced的情况。缺点是需要分类的次数多，时间复杂度和空间复杂度可能都比较高。

总结

本节课主要介绍了分类问题的三种线性模型：linear classification、linear regression和logistic regression。首先介绍了这三种linear models都可以来做binary classification。然后介绍了比梯度下降算法更加高效的SGD算法来进行logistic regression分析。最后讲解了两种多分类方法，一种是OVA，另一种是OVO。这两种方法各有优缺点，当类别数量k不多的时候，建议选择OVA，以减少分类次数。