最短路径之Dijkstra(迪杰斯特拉)算法（无向图）

简介

 

     Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。由for循环可知，其时间复杂度是O（n^2）。

 

原理

 

      在已知图的邻接矩阵net.vexs[i][j](无向网，含权值的图)的条件下，通过遍历已知图的所有路径，用dis[i]数组来记录到i点的最短路径，然后在循环中不断判断更替。首先，将所有点的集合分为俩部分，一边是已经遍历过的，另外一边是没有遍历过的，分别用mark[i]=1、mark[i]=0来表示。

 

代码通解

 

             在下面代码中，先将赋予初始值dis[i]=INF(无穷大)、mark[i]=0（未标记），而后单独将源点（x）所联通的路径权值net.arcs[x][i]赋予dis[i](

                                                          ①寻找遍历到点联通路径（与之相连线的点）中权值最小的一条； 标记遍历点；

                                                          ②修正最短路径；

而后，便是已经遍历所有点了，dis[i]也在不断的修正中得到真正的最小值，即最短路径。详情看下列代码：

 

 

#define MAXSIZE 20
#define PLACENUM 12
#define INF 9999           // 此处定义999为无穷大

struct
{
    int vexnum,arcnum;  //节点数和边数
    int vexs[MAXSIZE];      // 节点名
    int arcs[MAXSIZE][MAXSIZE];   //俩个节点之间的值
} net;
/*补充的结构体net,2019.7.3*/

void Dijkstra(int x,int y)      // x为源点，y为终点
{
    int i,j,k;
    int min;
    int u;   //下一个放入集合p的点
    int dis[net.vexnum];   //  最短路径
    int mark[net.vexnum];   //   被mark的便是已经遍历,未被mark的便是未遍历
    /*首先进行最短路径初始化*/
    for(i=0; idis[i])      //判断未遍历点 且 被赋值的最短路径（dis[i]dis[u]+net.arcs[u][i])                 // ！mark[i]判断不去走回头路，         //                                                                                dis[i]>dis[u]+net.arcs[u][i]有俩个用途：①若u链接的是x源点没有赋值最短路径的点，那么这里可以赋值②若是赋值过的点，那么可以判断是上一个dis[i]（此时是被赋值过的）是不是真正的最短路径，即修正。

            {
                dis[i] = dis[u] + net.arcs[u][i];      //若A->C比A->B->C更长那么A->B->C则是到C的最短路径，下图将解释。
         
                   }
             }
    }
     printf("最短路径值为：             %d",dis[y]);
}

 

 

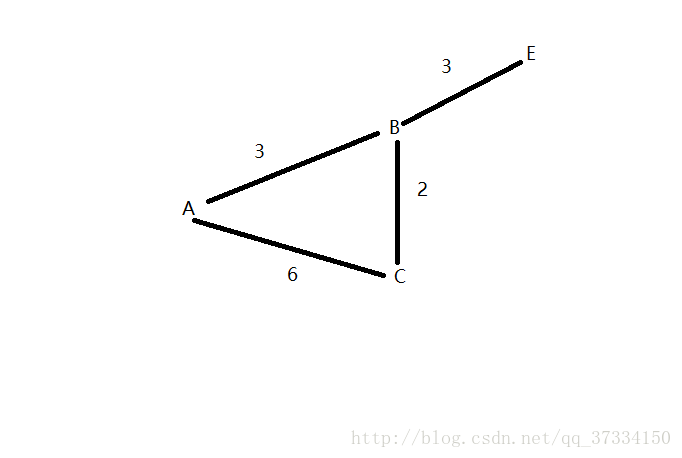我们以A，B，C三个点来举例子，三个点的最短路径分别为dis[0]、dis[1]、dis[2]。

 

 

                                                   ①A为源点初始化，dis[B]=3 (到B的最短路径，dis[1]),  dis[C]=6；

                                                   ②dis[B]

                                                   ③E未赋值，赋予dis[E];  C被之前赋予过,比较  dis[C] > dis[B] + net.arcs[B][C] (要不然你根本进不了这儿)，重新赋值dis[C] = dis[B]+net.arcs[B][C];

                                                   ④大循环遍历所有点，走遍天下。

 

 

 

 

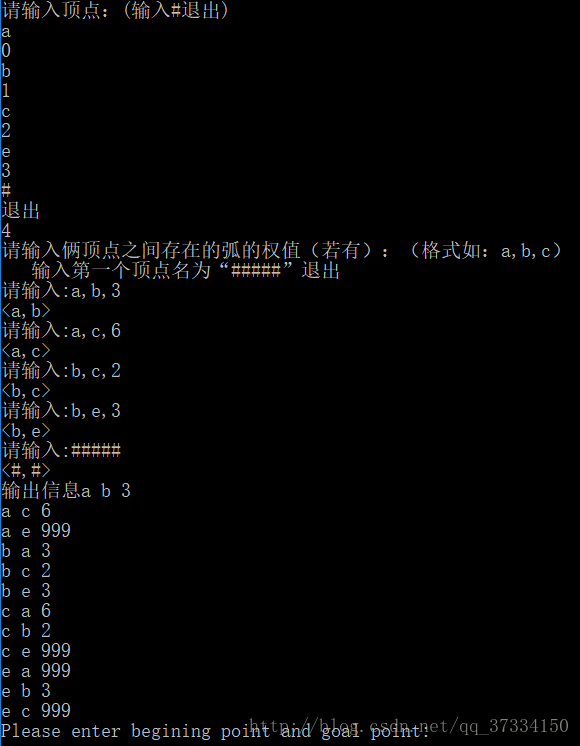
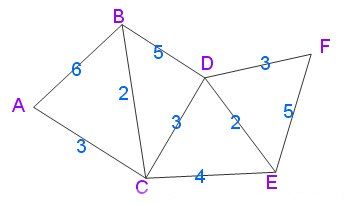
我觉得下面几张图很不错，图片取自https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html

图一

 

 

 

 

图二

 

19.3.24

关于修正最短路径

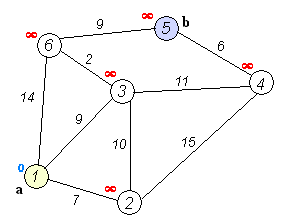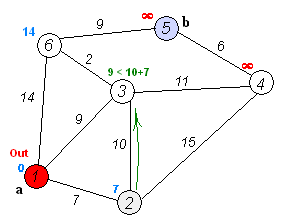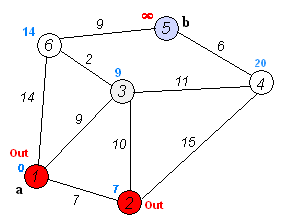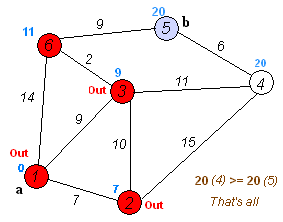
请参考一下文中引入的动图（图一）和表格图（图二），迪杰斯特拉求最短路径是，将需要遍历的点集合一个个进行遍历的。！mark[i]是需要其值为false(尚未遍历到，这是相对于当前遍历点)，当然，这就实现了它不会往回走，同时记录它“向前走”的最短距离点u，在其基础上（修正循环），与u点相连的未被标记（遍历到）的点记其中一个为z，判断源点x->z点们的dis（最短）值是否大于x->u->z点们的距离，如果大于，更新z点们的最新（新的路径）最短距离，在已知最短距离的情况下然后进行更新，直到遍历完所有的点集合（所有路径）。从源点往外辐射就能够理解了。

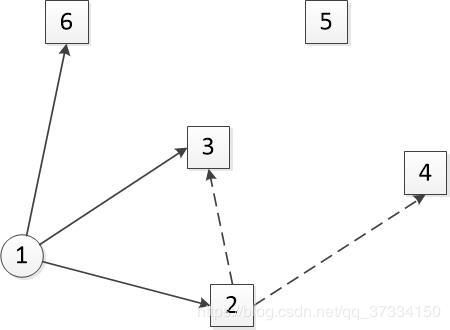
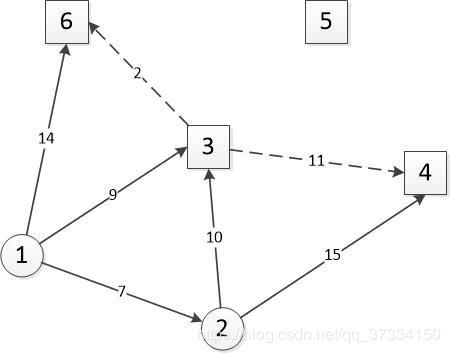
比如说1，2，3为三角形相互联系。当前是2。已经遍历了1，赋予了1->2、1->3、1->6的dis值，那么在修正部分就会从u(设12、13、16中12距离最小)，也就是2往外与没遍历且相邻的3和4判断以下：1->3大于1->2->3?  1->4大于1->2->4?，如果大于，更新dis值，此为修正，这里在已知最短距离1->2的基础上修正了1->3和1->4的dis值。同理到3的时候会修正源点(x/1)到4和到6的最短距离。

下图圆形为已遍历点，方形为未遍历的集合数据，实线为相邻连线，虚线为修正过程。

PS：mark是已经被找过从该点出发的相邻路径，修正在已知最短距离的情况下(u)，进行辐射，也就相对于找了u的所有相邻路径来比较更新（!mark[i]&& dis[i]>dis[u]+net.arcs[u][i]），但他并未记录u辐射的路径中的相邻最短路径（需要大循环）。

遍历第一个点——1的过程

 

遍历点2的过程

如果看懂了点个赞，给点小动力，谢谢啦~