泰坦尼克的沉没是历史上最臭名昭著的海难。1912年四月5日,在她的处女航上,泰坦尼克由于撞上冰山而沉没,2224人中的1502人葬身海底。由此而引起关注的海洋安全管理条例以及以后的几部著名电影不在本文讨论范围,这里也不会涉及英国白星航运公司为了获得保险理赔而偷梁换柱的阴谋论说法,虽然听起来很激动人心。
本文是kaggle上机器学习入门的一篇实践笔记。目的是从给出的891行训练数据(包含乘客或海员信息,以及是否生还)中训练数据模型,用它来预测其他418条记录的乘客的生存情况。
起初拿到这个题目时,真是无处下爪。从统计概率到微积分,学习难度只能说是平滑过渡,突然kaggle的Titanic自称是机器学习的入门练习,难度陡增不说,主要是这心里觉得难,既有点小鸡动更多的还是迷茫。于是打算看Andrew Ng在网易空开课的机器学习课程,然后,发现ML需要的预科课程比较多,比如线性代数,然后有去看线代。后来发现自己的方法论有问题,学习不应该是在实践中学习吗。好在很快就在网上找到一篇泰塔尼克这篇练习的详细教程,如果没有猜错,就是何明科翻译的Trevor Stephens的文章,可惜只翻译了第一章,后面的只能看原文,尝试了下,发现原文写的通俗易懂,照着做呗。
作者从最基本的安装环境讲起,甚至各种教科书都不会讲的语法,用对待5岁小孩的语气,非常适合我这样的初学者。
DAY 1 加入kaggle
首先是注册kaggle,在上面报名Titanic的比赛,这个比赛是kaggle上的入门案例,没有奖金,也没有勋章。下载数据集,一共有3个文件:train.csv是训练数据,含有Survive生还信息。test.csv是要预测的内容,还有一个gender_submission.csv好像是标准答,不确定。
将数据导入R中,并预览一下。
train<-read.csv(file.choose(),stringsAsFactors=F)
str(train)
test<-read.csv(file.choose(),stringsAsFactors=F)
str(test)
---------------------------------
'data.frame': 891 obs. of 12 variables:
$ PassengerId: int 1 2 3 4 5 6 7 8 9 10 ...
$ Survived : int 0 1 1 1 0 0 0 0 1 1 ...
$ Pclass : int 3 1 3 1 3 3 1 3 3 2 ...
$ Name : chr "Braund, Mr. Owen Harris" "Cumings, Mrs. John Bradley (Florence Briggs Thayer)" "Heikkinen, Miss. Laina" "Futrelle, Mrs. Jacques Heath (Lily May Peel)" ...
$ Sex : chr "male" "female" "female" "female" ...
$ Age : num 22 38 26 35 35 NA 54 2 27 14 ...
$ SibSp : int 1 1 0 1 0 0 0 3 0 1 ...
$ Parch : int 0 0 0 0 0 0 0 1 2 0 ...
$ Ticket : chr "A/5 21171" "PC 17599" "STON/O2. 3101282" "113803" ...
$ Fare : num 7.25 71.28 7.92 53.1 8.05 ...
$ Cabin : chr "" "C85" "" "C123" ...
$ Embarked : chr "S" "C" "S" "S" ...
其中:
- PassengerId 乘客编号
- Survived 是否生还,0表示死亡,1表示生还
- Pclass 船票等级,1表示Upper ,2表示Middle,3表示Lower
- Name 姓名
- Sex 性别
- Age 年龄
- SibSp 兄弟姐妹或配偶(在船上)的数量
- Parch 父母或子女(在船上)的数量
- Ticket 船票编号
- Fare 票价
- Cabin 船舱号
- Embarked 登船位置C瑟堡, Q昆士城, S南安普敦
然后我们查看一下生还信息统计。
table(train$Survived) %>%
prop.table()
这里我用了dplyr包中的管道函数%>%,因为非常好用就拿来了。管道表示将上一个函数的结果传递给下一个函数的第一个参数,R中很多函数第一个参数往往就是需要处理的数据集。
0 1
0.6161616 0.3838384
结果显示,在训练数据的891条记录中,生还比例只有38%左右,剩余的62%的人死光了。
通过上面这条信息,我可以简单的推测测试数据test中死亡比例很可能就是62%,比赛要求是提交每一个人的具体生还情况,live or die所以我这里听作者的话,竞猜全部死亡。然后生成要提交的数据框,再用write.csv()生成csv文件。
test$Survived <- rep(0,418)
submit <- data.frame(PassengerId = test$PassengerId, Survived = test$Survived)
filename = paste(getwd(),"output","theyallperish.csv",sep = "/")
write.csv(submit,file = filename,row.names = F)
生成的文件在output文件夹下,在kaggle上提交。
得分0.62679,也就是准确率62.6%。排名7116,原文中是1165由此可见一千名到七千名分数相同,所以只要稍微提高准确率,名次就会有极大地提升。就这样,比赛用最偷懒的方式完成了,今后就剩下提高名次。
DAY 2 性别,船费信息分类
这次加上性别信息,查看不同性别的生存概率:
train$Sex <- as.factor(train$Sex)
summary(train$Sex) %>%
prop.table()
---------------------
female male
0.352413 0.647587
以上男女比例。
取决于性别的生存率:
#two way comparison
prop.table(table(train$Sex,train$Survived),1)
--------------------
0 1
female 0.2579618 0.7420382
male 0.8110919 0.1889081
Okay, 大多是的女性活下来了,而只有少数男性。所以上次的预测是所有人都见阎王了,可以修正一下——所有女性都活下来了。
test$Survived <- 0
test$Survived[test$Sex == "female"] <- 1
str(test)
submit2 <- data.frame(PassengerId = test$PassengerId,Survived = test$Survived)
filename <- paste(getwd(),"output","sexprediction.csv",sep="/")
write.csv(submit2,file=filename,row.names = F)
这次的正确率0.76555,排名在5000左右,比上次上升了近2000。
紧接着,将目光聚焦在年龄上。
summary(train$Age)
--------------------
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.42 20.12 28.00 29.70 38.00 80.00 177
之前做决策的变量包含少数几个选项,但是年龄age包含连续的数值,所以将年龄按照一定的gap分组比较好。根据这次逃生的原则“女人和儿童优先”,我就来看看18岁以下而存活率是否好点。
首先添加一个字段,表示是否为儿童。
train$Child <- 0
train$Child[train$Age < 18] <- 1
查看存活人数
aggregate(Survived ~ Child + Sex,data = train,FUN = sum)
---------------------------
Child Sex Survived
1 0 female 195
2 1 female 38
3 0 male 86
4 1 male 23
但是看不出比例啊。要知道存活人数占该类别总人数的百分比~
aggregate(Survived ~ Child + Sex,data=train,FUN = length) #人数
------------------------------
Child Sex Survived
1 0 female 259
2 1 female 55
3 0 male 519
4 1 male 58
求百分比的话,需要自定义函数进行计算。这里用了我最喜欢的匿名函数(^_^)
aggregate表示:在data数据集中,对Survive字段,依据Child和Sex进行分组计算,计算方式是FUN,在FUN中, x是data中每一列的记录。
aggregate(Survived ~ Child + Sex,data=train,FUN = function(x){sum(x)/length(x)})
-----------------------------
Child Sex Survived
1 0 female 0.7528958
2 1 female 0.6909091
3 0 male 0.1657033
4 1 male 0.3965517
男孩的存活率确实高了点,但仍然不到40%,相比于女孩69%不足以改变我们的预测。下面试着将等级和船票费用加入考虑。
等级很标准的分为三个类别。而船费就没这么规整了,这里的处理方式跟上面年龄类似,分为
- 小于10
- 大于10,小于20
- 大于20,小于30
- 大于30
train$Fare2 <- "30+"
train$Fare2[train$Fare < 30 & train$Fare >= 20] <- "20-30"
train$Fare2[train$Fare < 20 & train$Fare >= 10] <- "10-20"
train$Fare2[train$Fare < 10] <- "<10"
然后求出依据等级和船费分组的生存率,并进行排序
sv<- aggregate(Survived~ Fare2 + Pclass + Sex, data=train,
FUN=function(x){sum(x)/length(x)})
sv[order(sv$Survived),]
---------------------
Fare2 Pclass Sex Survived
10 <10 1 male 0.0000000
13 <10 2 male 0.0000000
17 <10 3 male 0.1115385
9 30+ 3 female 0.1250000
19 20-30 3 male 0.1250000
14 10-20 2 male 0.1587302
15 20-30 2 male 0.1600000
16 30+ 2 male 0.2142857
18 10-20 3 male 0.2368421
20 30+ 3 male 0.2400000
8 20-30 3 female 0.3333333
12 30+ 1 male 0.3837209
11 20-30 1 male 0.4000000
7 10-20 3 female 0.5813953
6 <10 3 female 0.5937500
1 20-30 1 female 0.8333333
4 20-30 2 female 0.9000000
3 10-20 2 female 0.9142857
2 30+ 1 female 0.9772727
5 30+ 2 female 1.0000000
不知道为什么,船费大于30,且等级为lower(Pclass=3)的女性生存状况不太理想
9 30+ 3 female 0.1250000
....
8 20-30 3 female 0.3333333
对结果进行修正
test$Survived[test$Sex == 'female' & test$Pclass == 3 & test$Fare >= 20] <- 0
提交之后,结果是77.99%的正确率。排名3791。
五天前提交的,已经被挤下了42名,kaggle的排名是实时更新的。
DAY 3 决策树
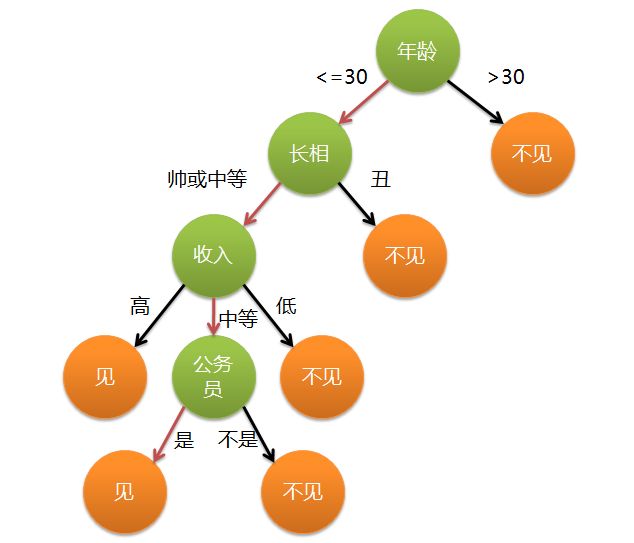
这次,我们要使用一个新的工具——决策树。什么是决策树?简单的说就是对分类问题进行概率预测。我看过最经典的解释是关于找对象的:
- 第一个标准是年龄——30岁以上的不考虑,直接淘汰;
- 在满足1的情况下,长得丑的不考虑;
- 1、2都满足,看收入,收入太低绝对不行;收入高的话,恩;
- 如果收入勉强凑合——那就要看是不是公务员啦。
严格意义上的决策树,每个指标都应该是可量化的,比如收入在5000以上?小于10000?这里5000和10000就是分割点。
构造决策树的关键在于选定分裂点,也就是上面的年龄,收入等。问题在于先哪个,后哪个。一个好的分裂点应该是能够将分组后的数据尽可能纯。这上面有很多算法比如ID3、C4.5等等看得我脑仁疼。
在这个决策树上。最顶部的年龄节点是所谓的根节点,所有参与“评选”的成年男性都会被年龄分组。所有橙色的节点是叶子节点,任何一个candidate经过分组,都会最终被安置在某一个叶子节点中。
笔者在这里不得不指出,决策树的一些缺陷。使用某些节点作为分裂点确实可以将结果集分得更“纯”,但是在整个决策树都完成,或者除非系统能够列出所有可能决策树,并评比每种可能的方案之前,没人知道那种是最好的。由此而产生了贪婪算法。
假设在一个虚拟的世界,收银员需要给顾客找零。这个奇葩的世界只有25元,15元和1元。现在顾客需要找零30。贪婪算法会告诉收银员:
- 小于30的最大币值 也就是25来找零
- 对余下的钱,重复上一条
最终的结果就是 25+1+1+1+1+1,花了6步才完成了找零任务;
最优的方案应该是 15+15 只需要2步完成。
除此之外决策树还有还有过度拟合的倾向,暂时略过。。。
开始构建我的第一个决策树吧!R提供了自带的包rpart(Recursive Partitioning and Regression Trees)封装了决策树函数。
在之前的练习中,我对年龄、等级和船费进行了分析,还有一些变量,比如同辈,长辈,登船位置等,没有涉及。船票编号后面是否隐藏着细腻的信息?让我们通过构建决策树来一探究竟。一下是原文中rpart函数的用法说明。
The format of the
rpartcommand works similarly to theaggregatefunction we used in tutorial 2. You feed it the equation, headed up by the variable of interest and followed by the variables used for prediction. You then point it at the data, and for now, follow with the type of prediction you want to run (see?rpartfor more info). If you wanted to predict a continuous variable, such as age, you may usemethod="anova". This would run generate decimal quantities for you. But here, we just want a one or a zero, somethod="class"is appropriate:
rpart的参数有些类似于aggregate,首先是方程式参数,由因变量~自变量1+自变量2+...的格式组成,data表示数据来源,紧接着是预测类型(详情查询?rpart),对于连续型变量比如年龄,可以使用method="anova"对数值进行十进制计算,对于0或1的分类,使用method="class"就足够了。
对变量进行决策树分组:
fit <- rpart(Survived ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked,
data=train,
method="class")
------------------------------
> fit
n= 891
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 891 342 0 (0.61616162 0.38383838)
2) Sex=male 577 109 0 (0.81109185 0.18890815)
4) Age>=6.5 553 93 0 (0.83182640 0.16817360) *
5) Age< 6.5 24 8 1 (0.33333333 0.66666667)
10) SibSp>=2.5 9 1 0 (0.88888889 0.11111111) *
11) SibSp< 2.5 15 0 1 (0.00000000 1.00000000) *
3) Sex=female 314 81 1 (0.25796178 0.74203822)
6) Pclass>=2.5 144 72 0 (0.50000000 0.50000000)
12) Fare>=23.35 27 3 0 (0.88888889 0.11111111) *
13) Fare< 23.35 117 48 1 (0.41025641 0.58974359)
26) Embarked=S 63 31 0 (0.50793651 0.49206349)
52) Fare< 10.825 37 15 0 (0.59459459 0.40540541) *
53) Fare>=10.825 26 10 1 (0.38461538 0.61538462)
106) Fare>=17.6 10 3 0 (0.70000000 0.30000000) *
107) Fare< 17.6 16 3 1 (0.18750000 0.81250000) *
27) Embarked=C,Q 54 16 1 (0.29629630 0.70370370) *
7) Pclass< 2.5 170 9 1 (0.05294118 0.94705882) *
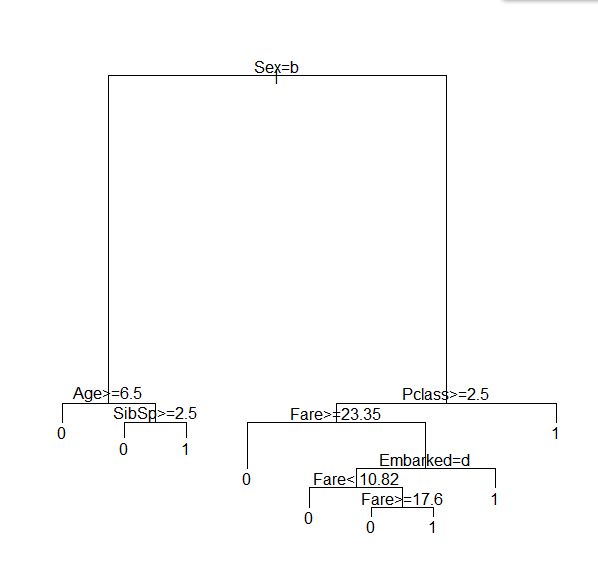
查看了下输出,原来节点的形式,基本上每个叶子节点的概率都已经很接近0或1了,简单可视化一下
plot(fit)
text(fit)
不忍直视。。
#整俩新包
install.packages('rattle')
install.packages('rpart.plot')
install.packages('RColorBrewer')
library(rattle)
library(rpart.plot)
library(RColorBrewer)
#输出
png("kaggle\\output\\dtree.png")
#一个更好的可视化
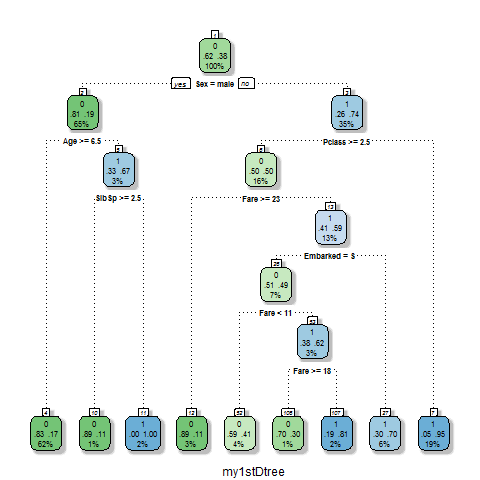
fancyRpartPlot(fit,sub = "my1stDtree")
dev.off()
这样生成的决策树非常美观,比我们之前手动判别的要更详细。基于决策树生成答案的过程也相当便捷:
#生成答案
Prediction <- predict(fit, test, type = "class")
submit4 <- data.frame(PassengerId = test$PassengerId,Survived = Prediction)
filename <- paste(getwd(),"kaggle","output","myfirstdtree.csv",sep="/")
write.csv(submit4,file=filename,row.names = F)
rpart中的预测函数predict(),参数1匹配模型对象,包含上面决策树的决策,应用在test数据框中,它会自动根据原始的参数生成预测结果中的数据,如果出错,也会指出错位的原因。最后我们生成了需要提交的预测文件。
最终准确率提高了0.5%,名次上升了434名,等级越高,小数点后几位的数字也就越重要!
rpart默认限制了决策树的深度,否则预测结果可能会出乎意料的反常。
但是,既然提升树的复杂度可以提高我们的名次,何不试着再深入一些呢??rpart.control查看树的限制信息,我们发现cp参数限制了一些不重要的节点的使用,设置cp=0可以暂时屏蔽限制。另一个需要开启的模式是minsplit,决定了最终有多少乘客被分配在同一个节点中(在再次分隔之前)。设置为2可以最精细分隔。
生成新的决策树,输出图片。
overfit <- rpart(Survived ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked,
data=train,
method="class",
control=rpart.control(minsplit=2, cp=0))
png("kaggle\\output\\overfitdtree.png")
fancyRpartPlot(overfit,sub = "Dtree_overfit")
dev.off()
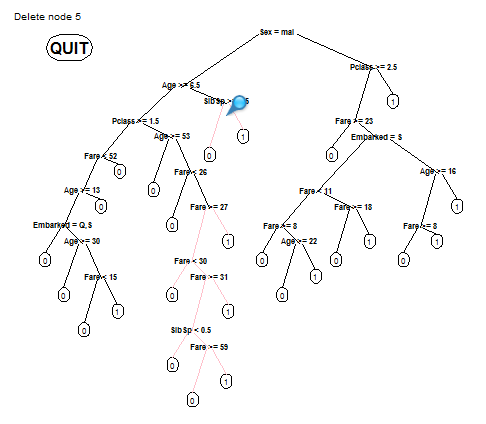
节点多到看不清&8&&&88&&888&888
在kaggle上提交
准确率只有74.1%?用最复杂的决策树生成的结果还比不上我们最开始的性别单变量预测(76.55%)?哪里出错了?
欢迎来到过度拟合的世界!
过度拟合,在学术上的定义是,对于训练模型,它能够以非常高的比率匹配,但是对于未知的数据却表现的很糟。刚刚我们构建了一个规则过于复杂,层次过深的决策树,对原始数据来说,可能他是100%匹配的,但是例子中34岁的底层妇女买了一张较贵的船票仅仅是个特例,但最终却影响到了我们的决策。
这个例子告诉我们一个道理,对于任何的算法,都要谨慎谨慎再谨慎,否则就是给自己挖坑。
另外,rpart允许生成一个可交互的决策树模型,用户选择那些节点可使用:
fit <- rpart(Survived ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked,
data=train,
method="class",
control=rpart.control(cp=0))
new.fit <- prp(fit,snip=TRUE)$obj
fancyRpartPlot(new.fit)
点击QUIT,新的决策树模型将会保存在new.fit对象中。
DAY 4 特征工程
特征工程对于模型的表现是如此的重要,以至于一个拥有更良好特征的简单模型胜过一个有着复杂的算法,但是特征不那么有用的模型。事实上,特征工程被描述为简化最重要的向量来决定你的模型是否有效。特征工程实际上可以归结为机器学习中的人为因素。个人对数据的理解程度,直觉和创造力,往往很重要。
那么什么是特征工程呢?针对不同的情况有不同的解释。在泰坦尼克这个案例中,特征工程指的是,通过截曲,合并数据等方式,对kaggle提供的数据进行压榨,以获得一些新的数据。一般来说,相比于那些没有处理过的数据,工程化的特征有助于机器学习算法更好的消化数据,创建模型。
为了获取更多的机器学习的更多魔力,我们开始关注那些在之前的预测中没有使用过的变量。每个人的船票号、舱号,和名字都是不同的。假如能在这些字符串中找到某种的规律,我们就可以提取出新的预测属性。
从姓名开始,看一下编号为1的用户姓名:
> train$Name[1]
[1] "Braund, Mr. Owen Harris"
如果我们概括看一下数据集的姓名信息,会发现称谓包含了Miss,Mrs,Master甚至Countess(女伯爵),Master这个称呼如今稍微有些过时,在哪个时代,Master指的是未结婚的男孩。另外,像Countess这样的贵族跟无产阶级的命运应该有所不同。以上应该是出了年龄,性别,社会等级的组合之外,我们还能发现的一些显而易见的信息。
为了获得新的变量,并应用到测试集上,需要将测试集和训练集合进行合并。
#合并要求两个或两个以上数据集的字段应当相同。
test$Survived <- NA
combi <- rbind(train, test)
然后是将姓名进行分割,使用函数strsplit
> strsplit(combi$Name[1], split='[,.]')
[[1]]
[1] "Braund" " Mr" " Owen Harris"
参数split中的是正则表达式,表示在逗号和点号中选一个。我发现!生成的名字前面有一个奇怪的空格,那是因为用来分割的点号后有一个空格。我还发现!整个string是包含在index[[1]] 里的,这是因为strsplit用双重叠加矩阵来生成结果,它不确定给的正则中是否有相同的块,如果有的话,避免覆盖原始值,它会在后面追加索引保存数据。为了取出他的称谓:
> strsplit(combi$Name[1], split='[,.]')[[1]][2]
[1] " Mr"
很好,我们现在将整个title孤立出来了。那么怎样才能将这种操作应用到整个数据集上呢?幸运的是,R有一些极其有用的函数,可以同时将复杂的操作应用到每一行上。如果仅仅使用combi$Title <- strsplit(combi$Name, split='[,.]')[[1]][2],这种方式只会每一条记录的Title都设置为Mr,不出所料,R中的apply族函数可以实现将函数应用到向量或者数据框上的功能。
这里用sapply函数,将这一操作应用到整个combi数据框上。
combi$Title <- sapply(combi$Name, FUN=function(x) {strsplit(x, split='[,.]')[[1]][2]})
apply族的每个函数运作方式稍有不同,sapply在此最适合不过。第一个参数是参与运算的数据框,FUN是操作执行的函数,function中的x表示数据框中的每一列。
分组观测一下这个Title
> table(combi$Title)
Capt Col Don Dona Dr Jonkheer
1 4 1 1 8 1
Lady Major Master Miss Mlle Mme
1 2 61 260 2 1
Mr Mrs Ms Rev Sir the Countess
757 197 2 8 1 1
#去掉title之前的第一个空格
combi$Title <- sub(' ', '', combi$Title)
恩姆,这里有一些少见的称谓对我们的决策没什么帮助,Mademoiselle 和Madame 非常接近,所以把这些合并在同一个分组里:
combi$Title[combi$Title %in% c('Mme','Mlle')] <- 'Mlle'
%in%操作符检查一个变量是否包含在一个向量里,返回逻辑值TRUE,FALSE。
继续寻找冗余数据,分类过多也是一个问题。
男性这边,有的称谓确实让人羡慕:Captain, Don, Major 和Sir. 这些人要么身居要职,要么腰缠万贯。女同胞这边,有Dona, Lady, Jonkheer尤其Countess同样身世显赫。让我们把这些值也进行简化,以便决策树能更好的处理他们。
> combi$Title[combi$Title %in% c('Capt', 'Don', 'Major', 'Sir')] <- 'Sir'
> combi$Title[combi$Title %in% c('Dona', 'Lady', 'the Countess', 'Jonkheer')] <- 'Lady'
> table(combi$Title)
Col Dr Lady Master Miss Mlle Mr Mrs Ms Rev Sir
4 8 4 61 260 3 757 197 2 8 5
#然后将其转化为因子
combi$Title <- factor(combi$Title)
诶呦不错哦。现在看看有没有别的可以搞的。SibSb和Parch隐藏了登船家庭的大小。同辈数和长辈数加起来,再加上乘客本人就是他的家庭大小。假设家庭越大,共同挤在一个小船上存活的可能性越低,似乎挺合理的。
combi$FamilySize <- combi$SibSp + combi$Parch + 1
其他的呢?我们刚才考察了,似乎家族人数较多的很难幸免于难。有没有考虑过某些特定的家庭面临更多困难?可以试着取出每个人的姓氏,以此分组貌似可以找到同个家族的人,但是如果名字过于常见比如Johnson,可能是些没有血缘关系的人。事实上这艘船上Johnsons家族总共只有3个人,而其他的Johnson是单独旅行。组合处理姓氏和家族大小或许可以削弱这种影响。假如两个Johnson不在同一个家庭,那么他们的FamilySize很可能应该是不同的,尤其在这么小的范围内。首先把姓氏信息分离出来:
combi$Surname <- sapply(combi$Name, FUN=function(x) {strsplit(x, split='[,.]')[[1]][1]})
然后我们的做法是,将每个用户的FamilySize和Surname拼接在一起,组成另一个独立变量。称为FamilyID
combi$FamilyID <- paste(as.character(combi$FamilySize), combi$Surname, sep="")
paste函数像胶水一样将两个或多个变量连接在一起,参数sep决定用什么做胶水。在此之前,由于FamilySize是数值型变量,不能和字符串进行拼接,将其转换为字符即可。这个时候又遇到一个问题,那些单独旅行的Johnson同样会被生成一个相同的1Johnson字符串,显然他们并不是同一个家庭的成员,这里将那些FamilySize小于2的标记为Small:
combi$FamilyID[combi$FamilySize <= 2] <- 'Small'
#总览一下FamilyID人数信息
> table(combi$FamilyID)
11Sage 3Abbott 3Appleton 3Beckwith 3Boulos
11 3 1 2 3
3Bourke 3Brown 3Caldwell 3Christy 3Collyer
3 4 3 2 3
3Compton 3Cornell 3Coutts 3Crosby 3Danbom
3 1 3 3 3
3Davies 3Dodge 3Douglas 3Drew 3Elias
5 3 1 3 3
3Frauenthal 3Frolicher 3Frolicher-Stehli 3Goldsmith 3Gustafsson
1 1 2 3 2
3Hamalainen 3Hansen 3Hart 3Hays 3Hickman
2 1 3 2 3
3Hiltunen 3Hirvonen 3Jefferys 3Johnson 3Kink
1 1 2 3 2
我们发现还是有些瑕疵,比如3Appleton明明家族人数是3人,可是根据姓氏统计只有他自己。当然有可能他们家姓氏不同,这很合理啊。
接下来进行一些清理工作:
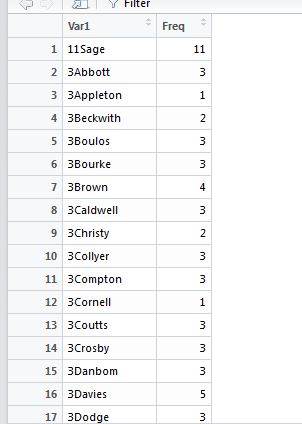
famIDs <- data.frame(table(combi$FamilyID))
现在这些信息存储在一个数据框中,如下
很可惜的是这些淘气的家庭信息并不按照我们预想的方式运行。取出那些非预想的,家庭人数较小的子集(我们的目的就是找出人数较小的家庭,在combi数据框中标注):
famIDs <- famIDs[famIDs$Freq <= 2,]
重写那些不正确的familyID,然后将整体转化为因子:
combi$FamilyID[combi$FamilyID %in% famIDs$Var1] <- 'Small'
combi$FamilyID <- factor(combi$FamilyID)
现在combi数据框中包含了两组新的变量,称谓Surname和家庭大小情况(小于3的被标记为small,其他的用数字+姓的方式标记)。准备好将数据分隔为训练集和测试集了,同时他们携带着Surname和FamilySize信息。上面那些工作的精妙之处在于,R是如何处理因子类型变量的。因子类型被计算机存储为整数类型的变量,只不过外表看起来像是字符串,字符和整数之间有着一一对应的关系,如果单独定义一个因子,跟数据集不连接的话。分离数据框之后,R不敢保证分离后的数据集都正确。
比如说,我们在combi数据框上添加了新的变量3Johnson,在分离之后的test数据框里虽然没有姓Johnson的乘客,但是整体的数据框也会保存因子信息,但如果因子是单独添加的,这时候test数据框中不包含姓为Johnson的乘客信息,用训练模型测试test数据时,由于数据的不一致会报错。
对数据进行分割:
train <- combi[1:891,]
test <- combi[892:1309,]
我们又有了新的变量,这下决策树会更高兴。
#生成决策树
fiteng <- rpart(Survived ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked + Title + FamilySize + FamilyID,
data=train,
method="class")
#可视化
png(paste(getwd(),"数据分析第四关","kaggle","output","engdtree.png",sep="/"))
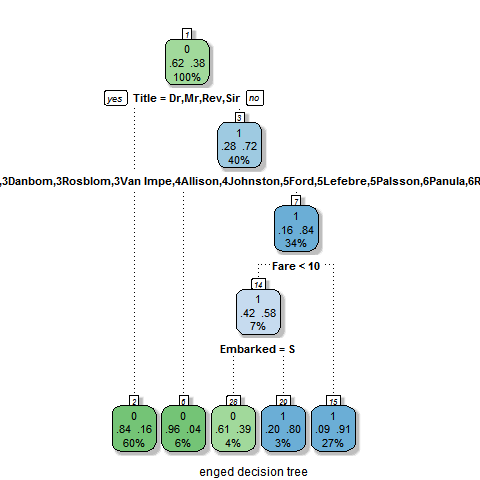
fancyRpartPlot(fiteng,sub = "enged decision tree")
dev.off()
有趣的是,新的变量主导了新的决策树,Title成了决策树的第一个分裂点,这里需要提一下决策树的另一个缺陷,它总是会倾向于使用等级更多的因子变量。但是不管怎样,我还是根据这个树进行预测并提交数据给kaggle,看一下准确率吧。
#生成结果
Prediction <- predict(fiteng, test, type = "class")
submit6 <- data.frame(PassengerId = test$PassengerId,Survived = Prediction)
filename <- paste(getwd(),"数据分析第四关","kaggle","output","engdtree.csv",sep="/")
write.csv(submit6,file=filename,row.names = F)
Bravo!这次的准确率提升了不到0.1%,但是名次提高了1719,直飙2000。
看来算法还是要在实践中不断领悟啊。
DAY 5 随机森林
随机森林,由数量庞大的决策树聚集而成。假设一个情景:在一个乐队里的某次表演中,如果有一个人在某个音符上演奏失误,很可能不会被察觉,因为他的声音被过于强大的主旋律所掩盖。随机森林也是这样,只要树的数量足够大,森林中的某一个决策树做出了错误的或偏差决策,并不会影响其他树的正确决策。最终结果会以少数服从多数进行表决。这些决策树或许算法不够完美,过度拟合,甚至选择了错误的分裂点,但如果我们组织一大群不相同的随机的决策树,让他们对结果进行投票,就可以超越这些限制。
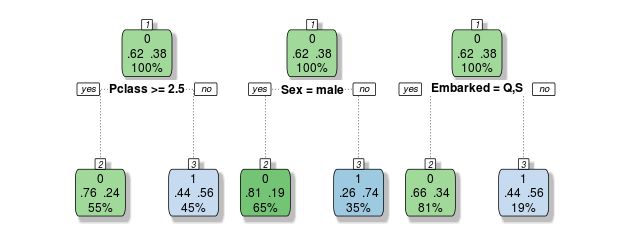
我们来做一个非常小的森林模型来进行说明:
以上三个决策树依据不同的单一变量进行分类决策。假如有一个来自Southampton的一等女乘客,树1和树2会预测她生还,单数树3给出相反的决策,三者投票表决,2:1 她活下来了。
当然真实的随机森林要比例子中的复杂得多,甚至都有着过度拟合的倾向。生成单个决策树的公式是固定的,但是随机森林要求每个树都不同,怎么才能做到呢?
- 方法一:bagging
这种方法将在可用变量中随机取出一些变量,生成一个组合,R中可用sample进行模拟:
> sample(1:10,replace = T)
[1] 9 6 10 6 3 8 4 6 7 3
在这个例子中,我们去了2个3,3个6,而4,7,8,9,10各一次,且每次执行都会有不同的结果。平均下来,约有37%的数字不会被取到,决策树的每一次生成,都会选择用一些轻微不同的变量,以保证没次都获得不用的结果。如果数据中某些特征过于强势,比如泰坦尼克例子中的性别问题,可能大多数决策树都会用这个作为第一个分裂点吧。为了解决这个问题,就要用到另一种方法。
- 方法二:
这种方法(在选择分裂点时)不会用整个变量池中选择,而是选取一个子集,这个子集的大小通常是整个变量池大小的平方根。比如我们友10个变量,每次只会在3个当中进行选择,在这种算法中,比如第一个分裂点要在年龄,船费,等级中进行选择,那么它打死也不可能选出性别来。
通过这两种方式生成的决策树,每一棵都会有不同的分类方法,而每棵树将给出他们自己的答案来,10个变量的排列组合就有10个数量级,得票多的获胜。每棵树都是过度拟合的,但是过度的方向不同,对他们进行平均,就能得到我们想要的结果。
如果说决策树是神通广大运筹帷幄的诸葛亮,那么毫无疑问随机森林就是臭皮匠,不是三个,而是成千上万个。
不过随机森林也有他的缺陷,那就是输入的数据集必须是干净的——即没有缺失值。决策树就没有这么严格的限制,rpart在处理缺失值时会自动替换为代理值。我么使用的训练数据或是测试数据中,有好多的乘客年龄缺失,决策树遇到这种情况,会使用其他变量代替,但是随机森林做不到。所以我们要手动替换这些缺失值。在第二天的实践中,在处理成人/小孩的分类中,曾经用平均数和中位数替换缺失值。不过我们已经学了新的工具,如今可以用决策树来填充那些缺失值了。
观测年龄特诊:
> summary(combi$Age)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.17 21.00 28.00 29.88 39.00 80.00 263
#1309人当中有263的年龄是缺失的,超过20%
#用其他变量来预测年龄
#method="anova"表示连续值
#预测年龄
Agefit <- rpart(Age ~ Pclass + Sex + SibSp + Parch + Fare + Embarked + Title + FamilySize,
data=combi[!is.na(combi$Age),], #依据年龄不为空
method="anova")
#可视化
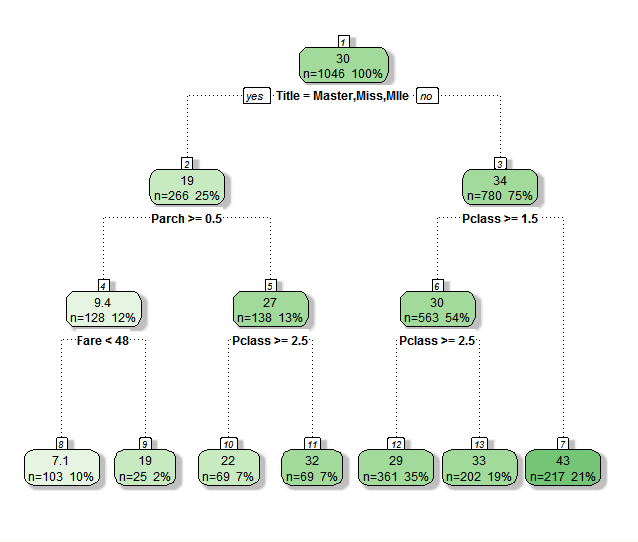
fancyRpartPlot(Agefit)
结果很有意思:
Title是Master,Miss,Mlle的年龄在30岁以上,如果有长辈同行,并且船费在48以下的,很可能是个小孩,那么他的年龄在7岁左右,很符合逻辑!
让我们把预测的结果赋值给缺失年龄的记录:
combi$Age[is.na(combi$Age)] <- predict(Agefit, combi[is.na(combi$Age),])
我没有使用家庭及大小和FamilyID因为我认为这些变量对年龄的预测作用不大。这时在观测年龄信息,发现缺失值不见了:
> summary(combi$Age)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.17 22.00 28.86 29.70 36.50 80.00
整体看一下数据还有哪些问题
> summary(combi)
发现Embark和Fare都有缺失值,有两个乘客的Embark字段是空白的。虽然说,空白值不会像缺失值na一样引发错误,但是既然我们是在清理数据,干嘛不把他干掉呢。2个对于1309来说是在是微不足道,不如把他设置成登入人数最多的一个港口吧。把这两个空白填上"S"代表Southampton。which表示满足某种条件的记录,返回值是记录索引:
> which(combi$Embarked == '')
[1] 62 830
#替换为S并转换为因子
> combi$Embarked[c(62,830)] = "S"
> combi$Embarked <- factor(combi$Embarked)
另一个是船票信息,有一个客户的船费信息丢失了
> summary(combi$Fare)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.000 7.896 14.454 33.295 31.275 512.329 1
将其替换为中位数
combi$Fare[which(is.na(combi$Fare))] <- median(combi$Fare, na.rm=TRUE)
随机森林的另一个限制是,不能处理等级level大于32的因子变量。而FamilyID几乎是这个值得两倍。现在我们有两条路可以走,第一是将3Johnson这类值替换成只包含数值的连续型变量,R中的unclass函数可以实现这一功能,另一条路是,手动缩减变量数量。我们选择第二条路,原先设置的将人数小于2的定义为Small,现在把这个门槛提高到3:
> combi$FamilyID2 <- combi$FamilyID
> combi$FamilyID2 <- as.character(combi$FamilyID2)
> combi$FamilyID2[combi$FamilySize <= 3] <- 'Small'
> combi$FamilyID2 <- factor(combi$FamilyID2)
预处理终于完成,可以将combi数据分隔为原始的train和test,以进行下一步:随机森林生成。
首先安装包并引入:
install.packages('randomForest')
library("randomForest")
在随机选取样本之前,设置一个随机数种子,这样可以保证今后再次这个运行脚本的时候,出现相同结果。否则每次的森林都不一样。
set.seed(225)
函数中的数字具体是多少并不重要,自己要今后在用的时候仍然是这个数就行了。随机森林的参数格式跟决策树相似,除了一些额外参数。
forest <- randomForest(as.factor(Survived) ~ Pclass + Sex + Age + SibSp + Parch + Fare +
Embarked + Title + FamilySize + FamilyID2,
data=train,
importance=TRUE,
ntree=2000)
这里多试了几下,刚开始报错
Error in randomForest.default(m, y, ...) : NA/NaN/Inf in foreign function call (arg 1)
网上查原因,发现randomForest对char类型无法自动转为factor,需要将变量转换为int, factor ,num类型。这里的参数importance=true可以让我们手动检查变量的重要性,之后会看到。ntree规定了我们要种多少颗树。如果你在使用一个非常大的数据集,ntree可以限制树的多少,nodesize限制节点的数量以避免树太过复杂,sampsize限制样本行的大小。mtry的默认值是用总变量数的平方根作为选取的变量数。
查看变量重要性:
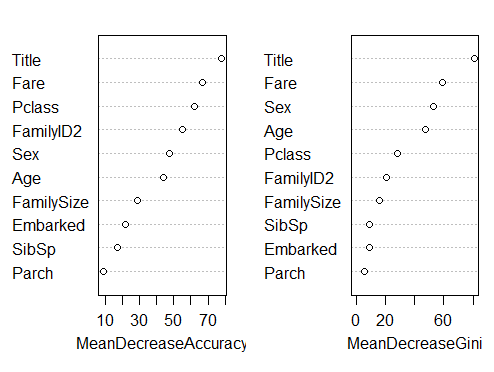
varImpPlot(fit)
[笑哭][笑哭]为啥原作者的图是酱紫的
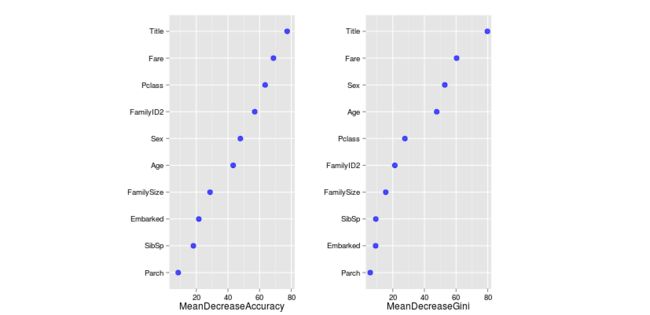
而我的是酱紫的
记得在生成森林时会有约37%的数据被遗漏,随机森林不会白白浪费这些数据,它会通过这些数据进行测试,以测评在未知数据上的命中率。
上面的图片展示了两种描绘重要性的方法,accuracy展示了当森林不包含当前变量时表现有多糟,表示没有他,预测的准确性会大大降低。另一种Gini系数挖掘决策树背后的数学关系,它本质上表现了叶子节点的纯净度。同样会测试没有这个节点会怎样,分数越高越重要。
随机森林的预测函数也跟决策树很相似,不过让2000颗决策树进行评比投票要花一些时间。
#生成结果
Prediction <- predict(fit, test,type="class")
submit7 <- data.frame(PassengerId = test$PassengerId, Survived = Prediction)
filename <- paste(getwd(),"kaggle","output","randomforest.csv",sep="/")
write.csv(submit7,file=filename,row.names = F)
结果不是很理想,哼。终于理解了那句:数据比算法更重要。数据集太小,生成的森林自然不够完善。
不过现在还不是放弃的时候,我们还有一种方法——条件推理树。不同于典型的决策树,条件推理树用的是统计测试而不是纯度测量,他们的基础结构是一样一样的。
party包中封装了这个方法:
install.packages('party')
library(party)
由于条件推理树对于因子没有level的限制,我们将使用原始的未合并的数据。同时生成森林的函数和预测函数的参数都有些不同:
set.seed(128)
predictfit <- cforest(as.factor(Survived) ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked + Title + FamilySize + FamilyID,
data = train,
controls=cforest_unbiased(ntree=2000, mtry=3))
Prediction <- predict(predictfit , test, OOB=TRUE, type = "response")
之前随机森林中设置树量的ntree现在在controls=cforest参数中,并且mtry需要手动设置,predict函数也需要设置OOB,即那遗忘的37%数据。
submit8 <- data.frame(PassengerId = test$PassengerId, Survived = Prediction)
filename <- paste(getwd(),"kaggle","output","conditioninference.csv",sep="/")
write.csv(submit8,file=filename,row.names = F)
太棒了!历时一个月,从最初的62.6%。排名7116,上升到80.86%,排名670。进到前10%,幸福啊。一步一步跟着教程走下来,终于结束了,还有点舍不得。好在Stephens推荐了接下来的路The Art of R Programming: A Tour of Statistical Software Design