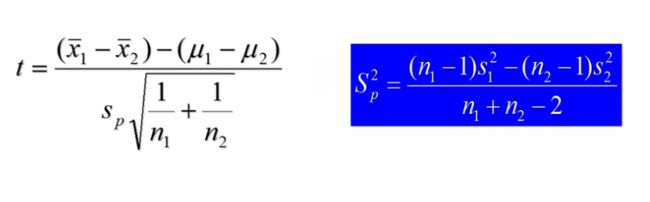本文是对 孟浩巍
生物信息学入门课:学习生信你需要了解的统计学课程的学习。
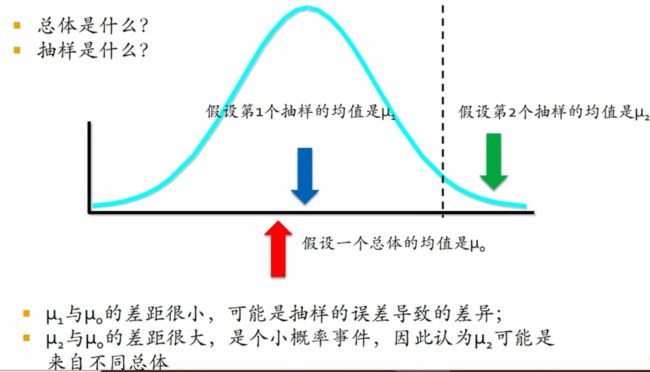
五. 假设检验
1. 假设检验基本介绍
K.Pearson——Sir Ronald Aylmer Fisher(女士品茶,Fisher线性判别,极大似然估计,试验设计)——Neyman and E Pearson.
Fisher的女士品茶提出来的小概率标准为0.05。
什么是假设?:通过MT和TM的假设确定总体的一些参数;什么是检验:判断假设是否成立,是否为小概率事件。
假设检验的一般步骤:
- 提出原假设H0和备择假设H1
- 确定适当的检验统计量(t检验/卡方/F检验)
- 计算出抽样结果的PValue
- 如果PValue很小(0.01/0.05),拒绝H0接受H1
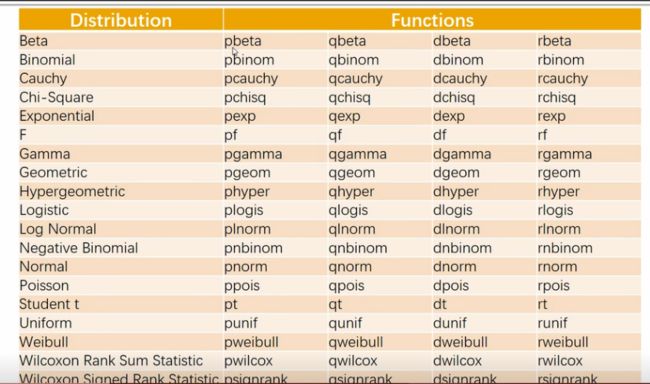
2. PValue的计算
R中计算PValue的相关函数:
- Beta分布——二项分布——柯西分布——卡方分布——指数分布——F分布——Gamma分布——几何分布——超几何分布——逻辑斯特分布——Log Normal分布——负二项分布——正态分布——泊松分布——T分布——均匀分布——威泊尔分布
- p(probability)概率分布,累计分布概率
- q(quantile)分位数计算,确定99%的分位数
- d(density)概率密度函数(概率密度函数y轴坐标取值)
- r(random)取对应分布的随机数
##确定分位数
qnorm(0.99,mean=0,sd=1) ##确定99%的分位数值
## 确定概率
pnorm(-1.96,mean = 0, sd =1) ## 0.024
pnorm(0,mean = 0, sd =1) ## 0.5
##概率密度函数曲线
plot(dnorm(seq(-10,10,length.out = 1000),mean = 0,sd = 1))
##模拟取值
rnorm(10,mean=5,sd=2)
###设置随机种子保证rnorm里取值一致。
sed.seed(2019)
rnorm(10,mean=5,sd=2)
在生物信息里的例子:
-
某次测序全基因组平均突变率为0.003,某个位点中检测到带有C的reads10条,带有T的reads为3条,那么该位点是否为一个甲基化位点?(background:原始的C,被清洗后不带甲基化位点为T,带甲基化(C被保护)位点为C)
- 二项分布:n=13, p=0.003
- 具体R中
pbinom(q=3,size = 13,prob = 0.003)
-
MACS2中call peak认为reads count在基因组某个区域的分布服从泊松分布,估算某一段区域中的Possion分布的参数?假设已经估算出lambda=5,如果一段区域内出现了20条reads,那么pvalue应该是多少?
- lambda估算:一段区域的reads count数出来,平均?或者估算整体基因组的lambda。
- x=20,21,22...出现抽样结果或者比抽样结果更极端的情况。加起来一起的pvalue即为次pvalue
- 具体R中计算
ppois(20,lambda=5)为累计概率。>20的pvalue1-ppois(20,lambda=5)
3. 统计功效和假设检验的两类错误
两类错误和统计功效:
1类错误假阳性,2类错误假阴性。α去真概率,β纳伪概率。
当样本量确定时,α和β是一个balance。α是定义的显著性水平,如0.01,pvalue实际是很小。而α定的十分小的情况下,β的犯错概率就大了。所以具体再平衡的过程中需要进一步考虑。例如在癌症检测时,会尽可能把H1都找出来,所以宁愿假阳性高,假阴性低,cutoff 甚至0.1。而相反的在call peak时要找到最真的peak
提高统计功效:加大样本量(较简单),更改统计方法。
4. 使用Pvalue常见的错误
1. 在任何时候都以0.05或者0.01作为金标准
- 有些统计检验如Fisher Exact test类(GO/KEGG/Motif计算)容易出现非常小的pvalue。一般会取10-4,认为取小于10e-4才算显著。
2. 设定Pvalue阈值时忽略了2类错误的犯错可能。
- 比如在病理确诊时 H0代表没病,H1代表有病。二类错误的假阴性更严重,所以设置α提高0.1/0.2,假阴性β就会降低。
3. 计算Pvalue过程中,忽略了使用假设检验的基本条件。
- 比如t检验(服从正态分布,两个样本方差齐。如果不服从原假设基本要求,而应用其它的如非参数检验)
4. 在使用PValue的时候,会忽略了假设检验的原假设。
- 仅能说是根据Pvalue发现有相关关系,但相关关系不大。
回归分析时,原假设的两个变量是不是有相关关系(没有/有 ),而具体相关关系的大小,归到回归中解释。
4. T检验相关内容
主要围绕正态分布进行。大样本Z-test,小样本T-test
1. Z-score和Z变换
- Z变换是已知了总体方差和总体均值的情况。其中在α=0.05时,Z=+-1.96,所以按公式计算完Z值之后再通过pnorm(z,mean=0,sd=1)转换。
2. 为什么有了Z test之后还要T test?:因为通常情况下我们很难获得总体方差(最多获得总体均值的估计),往往就想通过样本方差来代替总体方差。
## R中T-test值转换为Pvalue
1-pt(q=14.16,df=10-1)
- (当X均值-样本均值)/(样本方差/根号n),它是服从自由度n-1的student-T-test。自由度越高越服从正态分布,n越大越服从z test大样本统计。
- 大样本统计的n至少>=30(50),所以在一般情况下大都是进行T-test
3. T-test两种最常见的情况:
- 有一组试验样本数据,与已知标准均值去做比较
### 已知A基因在总体均值中为15,观察5个人中A(13.1,16.2,14.9,15.8,17.7),分析该病人基因A有无显著升高。
res <- c(13.1,16.2,14.9,15.8,17.7)
t.test(res,mu = 15,alternative = "greater") ##单端变大,所以alternative="greater"
- 两批独立随机试验结果,需要比较是否有差异(已知样本均值,样本方差相等)
- 两个样本是独立的随机样本(一般仪器测量的属于正态分布,有多个因素影响,而没有主效因素影响同属于正态分布)
- 两个总体都是正态分布
-
两个总体方差未知但相等(两批实验组内的variation不能过大)
### 2. compare two sample
geneB.ctrl <- c(12.33,7.56,11.47,9.82,9.14)
geneB.deoxy <- c(10.41,14.82,14.13,15.81,13.62)
t.test(geneB.ctrl,geneB.deoxy)
- 配对样本的均值比较T-test(如同组实验样本的前后进行比较,一个group比较用药前和用药后)作差,如果没差异的话是根0比较接近。即可根据公式进行检验。得出的T-test值后查表
### 3. paired t.test
before.fitness=c(94,101,110,103,97,88,96,101,104,116.5)
after.fitness <-
- 2组独立随机试验结果,在方差不相等的情况下做比较(应该首先用F检验来检查方差是否相等,在方差不相等的情况下,应该使用t'检验或者是Wilcox秩和检验)
### 4. compare two sample ,方差不相等
geneB.ctrl <- c(12.33,7.56,11.47,9.82,9.14)
geneB.deoxy <- c(3.41,14.82,14.13,15.81,4.62)
## 先F检验var.test检测两个样本内方差是否相等
var.test(geneB.ctrl,geneB.deoxy)
## t.test
t.test(geneB.ctrl,geneB.deoxy,var.equal = F)
## wilcox test
wilcox.test(geneB.ctrl,geneB.deoxy)
5. 列联表检验
生物信息中常见的列联表检验问题即GO/KEGG富集分析问题
- 利用R语言中的
chisq.test函数
# chisq test 2
ratio_vec = c(335,125,160)
prob_vec = c(9,3,4) / 16
chisq.test(ratio_vec,p = prob_vec)
- 大样本水平下,我们认为K近似服从卡方分布,从而进行卡方检验。小样本情况,即表格中理论频数小于5,加和样本总数n<40,应该使用Fisher exact test精准检验。而当理论频数大于5时,进行卡方检验
- Fisher exact test本质上是超几何分布检验,在生物信息上如富集分析,判断某位点是否为突变位点。
# fisher test
test_mat = matrix(c(55,200,200,19800),ncol = 2,nrow = 2)
fisher.test(test_mat)