正权图,貌似看来是一道裸的 \(dijkstra\)
\(dijkstra\)的主要步骤:
首先,在\(dijkstra\)中,源点表示一开始的出发点,蓝点表示还未确定的点,白点则表示已经确定的点。
第一步先确定源点,有时候题目会告诉你。
接下来第二步,通过当前点去更新其能到的点的最短距离,并把其标记为白点。
第三步,在一遍扫完后再次寻找一个当前还没有被使用过且离源点最近的蓝点,做下一次更新。
\(dijkstra\)的模拟过程:
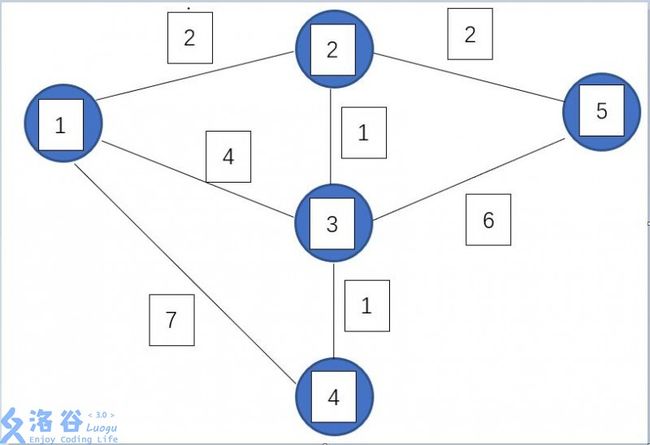
以下图为例:
一开始,所有点都是蓝点。\(dis[1]=0\),其余点均为 \(0x7f\)。
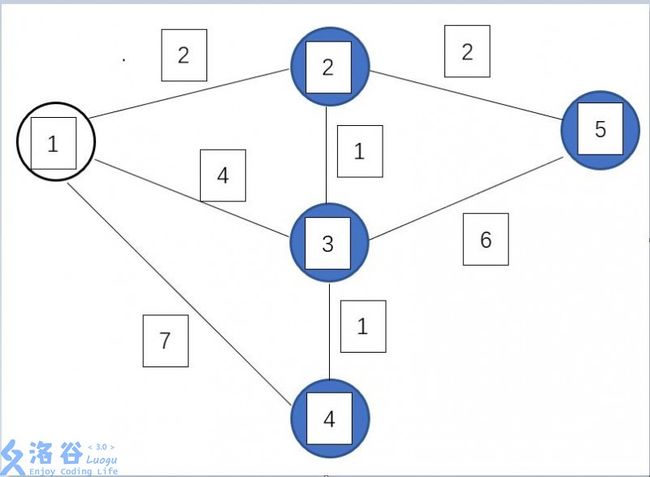
第一轮找到\(dis[1]\)最小,所以将\(1\)标为白点,得到新的\(dis[2]=2\),\(dis[3]=4\),\(dis[4]=7\)
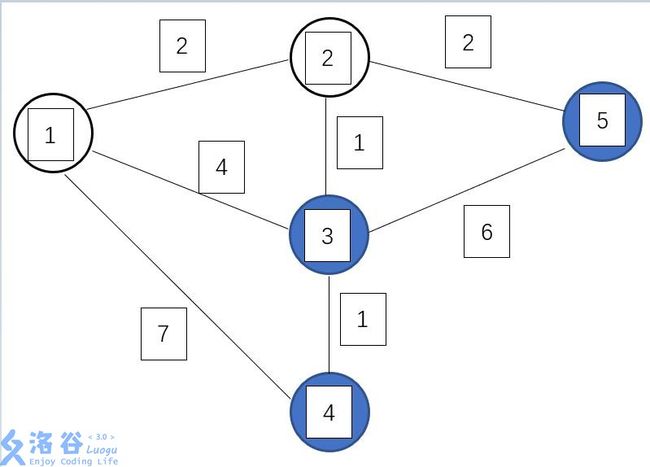
第二轮找到\(dis[2]\)最小,所以将\(2\)标为白点,得到新的\(dis[3]=3\),\(dis[5]=4\)
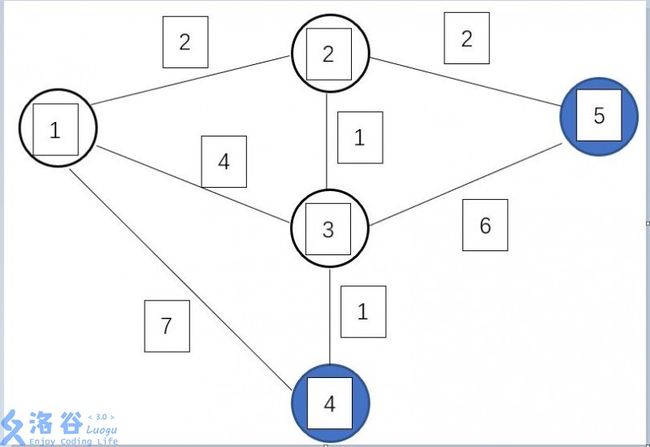
第三轮找到\(dis[3]\)最小,所以将\(3\)标为白点,得到新的\(dis[4]=4\)
最后两轮循环再将点\(4\)和点\(5\)变成白点即可。
所以最后的\(dis\)数组:
1 2 3 4 5
dis 0 2 3 4 4\(dijkstra\)的程序实现:
本题最后要求出每个点到源点的最短距离,显然就是跑一遍\(dijkstra\)然后输出\(dis\)数组即可。
朴素算法因为每次都要查找当前离源点最近的蓝点,时间复杂度会达到\(n^2\),不能过本题的数据,但还是可以把这道题\(A\)掉的。
于是我们来思考如何优化,很容易想到的一种方法就是用一个优先队列维护当前所有点离源点的距离,每次弹出最短的,直到出现蓝点为止。这样就省去了\(O(n)\)的寻找,总时间复杂度\(O(n+m\) \(log\) \(n)\)。
结构体的比较注意重载小于运算符哦\(qwq\)。
\(Code:\)
#include
using namespace std;
int n,m,s,dis[100010],vis[100010];
struct node{
int x,dis;
bool operator<(const node&a)const{//重载小于运算符
return dis>a.dis;
}
};
vector< pair >next[100010];//存边
priority_queueq;
void dijkstra(){
memset(dis,0x7f,sizeof(dis));//一开始所有值都设为最大值
dis[s]=0;
q.push({s,0});//源点
while(!q.empty()){
int Min=q.top().x;//每次弹出最短的
q.pop();//出队
if(vis[Min])continue;//不能是白点
vis[Min]=1;//标记
for(int i=0;idis[Min]+Nextw){
dis[Next]=dis[Min]+Nextw;//更新
q.push({Next,dis[Next]});//入队
}
}
}
}
int main(){
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
next[x].push_back(make_pair(y,z));//连边
}
dijkstra();
for(int i=1;i<=n;i++){
cout<