蒟蒻的\(DP\)很菜,\(SO\)我准备上一套二分的玄学操作
一.简单的二分答案
二分主要是用来解决一些最值问题,它可以有效的优化暴力,使复杂度减少到\(O(logn)\)。
我先给大家介绍一下二分里一个常用的模型:左闭右开。
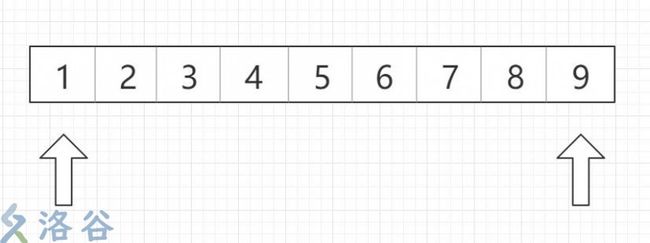
如图,这就是个典型的左闭右开模型。其中,黄色部分可以表示成一个区间 \([1,9\)}, 其中包含了数字\(1\)~\(8\),而并非包含\(9\),在二分里我们把它称之为“右开”。
那么回过头来看\(1\),它是区间内的值,也是开始的值\((a.begin())\),在二分里我把它称为“左闭”。
所以,在一个左闭右开的模型中,区间\([ll,rr\)}表示\(ll\)至\(rr-1\)内所有包含的值。
那么回到二分里,我们是不是可以把左边的\(ll\)标记成一定可以满足的值。右边的\(rr\)标记成一定不可以满足的值。那么我们就可以通过通过\(mid=(ll+rr)/2\)来取得中间值不断更新区间。如果\(mid\)可行,则\(ll\)至\(mid\)都可行,于是区间就缩小到了\([mid,rr\)}。如果\(mid\)不可行,则\(mid\)至\(rr\)都不可行,于是区间就缩小到了\([ll,mid\)}。
所以我们可以用一个\(while\)循环来不断更新区间(越来越小)。直到\(ll+1=rr\),说明\(ll\)可行,\(ll+1(rr)\)不可行,则停止。最后的\(ll\)就是一定可行的最大情况。
左闭右开 \(-\) 模板:
while(ll+1知道了左闭右开,左开右闭也不难理解了。在一个左开右闭的模型中,区间{\(ll,rr\)]表示\(ll+1\)至\(rr\)内所有包含的值。
所以,我们可以把左边的\(ll\)标记成一定不可以满足的值,右边的\(rr\)标记成一定可以满足的值。再通过\(mid\)不断更新区间,直到\(ll+1=rr\)。最后的\(rr\)就是一定可行的最小情况。
左开右闭 \(-\) 模板:
while(ll+1二. 实践
题意:\(n\)本书\(m\)个人,每人抄连续的几本书(不能不抄),求最后时间用的最多的那个人。
二分解题思路:
套一个表示复制时间的区间,逐一\(check\)是否可行。采用左开右闭的方式,一开始\(ll=0\)则一定不可行,\(rr\)等于这些时间的总和则一定可行。再不断取\(mid\)即可。
如何\(check\)
二分中的\(check\)须按题意模拟,本题中,我们可以通过二分给出的这个时间,来判断能否满足\(m\)个人就足够干完。所以循环跑一遍就行啦,主要是一些细节可以参考我的代码。
输出过程
如果已经二分得到了最小的复制时间\(rr\),我们就能倒推把每个人的复制区间找出来。但是由于要尽可能让前面的人少抄写,我们可以倒着循环,让后面的人复制到最大化,前面的人自然就少抄了。
\(Code:\)
#include
using namespace std;
int n,m,he,a[100010];
int s[1010],t[1010],len;
bool check(int x){
int tot=0,sum=1;//tot表示临时时间总和,sum表示人数
for(int i=1;i<=n;i++){
if(a[i]>x)return false;//如果打印一本的时间就不够,直接返回false
if(tot+a[i]<=x){
tot+=a[i];//连续当前的时间
}else tot=a[i],sum++;//时间不够用了,在来一个人
}
return sum<=m;
}
void Point(int x){
int tot=0,last=n;
a[0]=INT_MAX/2;//边界
for(int i=n;i>=0;i--){
if(tot+a[i]<=x){
tot+=a[i];
}else{
len++;
s[len]=i+1;
t[len]=last;//记录区间
last=i;
tot=a[i];
}
}
for(int i=len;i>=1;i--){
cout<>n>>m;
if(m==0)return 0;//说明没人来干活,程序直接结束
for(int i=1;i<=n;i++){
cin>>a[i];
he+=a[i];
}
int ll=0,rr=he;
while(ll+1