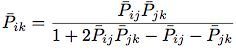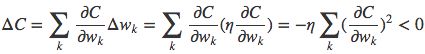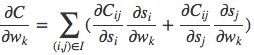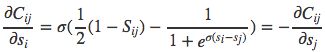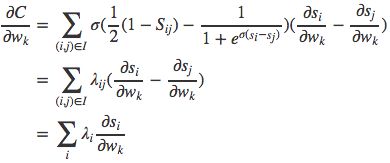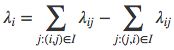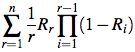1. RankNet
RankNet是2005年微软提出的一种pairwise的Learning to Rank算法,它从概率的角度来解决排序问题。RankNet的核心是提出了一种概率损失函数来学习Ranking Function,并应用Ranking Function对文档进行排序。这里的Ranking Function可以是任意对参数可微的模型,也就是说,该概率损失函数并不依赖于特定的机器学习模型,在论文中,RankNet是基于神经网络实现的。除此之外,GDBT等模型也可以应用于该框架。
1.1 相关性概率
我们先定义两个概率:预测相关性概率、真实相关性概率。
(1)预测相关性概率
对于任意一个doc对(Ui,Uj),模型输出的score分别为si和sj,那么根据模型的预测,Ui比Uj与Query更相关的概率为:
由于RankNet使用的模型一般为神经网络,根据经验sigmoid函数能提供一个比较好的概率评估。参数σ决定sigmoid函数的形状,对最终结果影响不大。
RankNet证明了如果知道一个待排序文档的排列中相邻两个文档之间的排序概率,则通过推导可以算出每两个文档之间的排序概率。因此对于一个待排序文档序列,只需计算相邻文档之间的排序概率,不需要计算所有pair,减少计算量。
(2)真实相关性概率
对于训练数据中的Ui和Uj,它们都包含有一个与Query相关性的真实label,比如Ui与Query的相关性label为good,Uj与Query的相关性label为bad,那么显然Ui比Uj更相关。我们定义Ui比Uj更相关的真实概率为:
如果Ui比Uj更相关,那么Sij=1;如果Ui不如Uj相关,那么Sij=−1;如果Ui、Uj与Query的相关程度相同,那么Sij=0。通常,两个doc的relative relevance judgment可由人工标注或者从搜索日志中获取得到(见http://www.cnblogs.com/bentuwuying/p/6681943.html)。
1.2 损失函数
对于一个排序,RankNet从各个doc的相对关系来评价排序结果的好坏,排序的效果越好,那么有错误相对关系的pair就越少。所谓错误的相对关系即如果根据模型输出Ui排在Uj前面,但真实label为Ui的相关性小于Uj,那么就记一个错误pair,RankNet本质上就是以错误的pair最少为优化目标。而在抽象成cost function时,RankNet实际上是引入了概率的思想:不是直接判断Ui排在Uj前面,而是说Ui以一定的概率P排在Uj前面,即是以预测概率与真实概率的差距最小作为优化目标。最后,RankNet使用Cross Entropy作为cost function,来衡量的拟合程度:
化简后,有:
当Sij=1,有:
当Sij=-1,有:
下面展示了当Sij分别取1,0,-1的时候cost function以si-sj为变量的示意图:
可以看到当Sij=1时,模型预测的si比sj越大,其代价越小;Sij=−1时,si比sj越小,代价越小;Sij=0时,代价的最小值在si与sj相等处取得。
该损失函数有以下几个特点:
当两个相关性不同的文档算出来的模型分数相同时,损失函数的值大于0,仍会对这对pair做惩罚,使他们的排序位置区分开。
损失函数是一个类线性函数,可以有效减少异常样本数据对模型的影响,因此具有鲁棒性。
总代价为:
其中,I表示所有在同一query下,且具有不同relevance judgment的doc pair,每个pair有且仅有一次。
1.3 合并概率
上述的模型Pij需要保持一致性,即如果Ui的相关性高于Uj,Uj的相关性高于Uk,则Ui的相关性也一定要高于Uk。否则,如果不能保持一致性,那么上面的理论就不好使了。
我们使用Ui vs Uj的真实概率 和 Uj vs Uk 的真实概率,计算Ui vs Uk的真实概率:
若,则有下图所示:
1.4 Gradient Descent
我们获得了一个可微的代价函数,下面我们就可以用随机梯度下降法来迭代更新模型参数wk了,即
η为步长,代价C沿负梯度方向变化。
这表明沿负梯度方向更新参数确实可以降低总代价。
1.5 加速RankNet训练过程
上面的是对于每一对pair都会进行一次权重的更新,其实是可以对同一个query下的所有文档pair全部带入神经网络进行前向预测,然后计算总差分并进行误差后向反馈,这样将大大减少误差反向传播的次数。
即,我们可以转而利用批处理的梯度下降法:
其中,
我们令:
有:
下面我们来看看这个λi是什么。前面讲过集合I中只包含label不同的doc的集合,且每个pair仅包含一次,即(Ui,Uj)与(Uj,Ui)等价。为方便起见,我们假设I中只包含(Ui,Uj)表示Ui相关性大于Uj的pair,即I中的pair均满足Sij=1,那么
这个写法是Burges的paper上的写法。下面我们用一个实际的例子来看:有三个doc,其真实相关性满足U1>U2>U3,那么集合I中就包含{(1,2), (1,3), (2,3)}共三个pair
显然λ1=λ12+λ13,λ2=λ23−λ12,λ3=−λ13−λ23,因此我所理解的λi应为
λi决定着第i个doc在迭代中的移动方向和幅度,真实的排在Ui前面的doc越少,排在Ui后面的doc越多,那么文档Ui向前移动的幅度就越大(实际λi负的越多越向前移动)。这表明每个f下次调序的方向和强度取决于同一Query下可以与其组成relative relevance judgment的“pair对”的其他不同label的文档。
同时,这样的改造相当于是mini-batch learning。可以加速RankNet的学习过程。
原先使用神经网络模型,通过Stochastic gradient descent计算的时候,是对每一个pair对都会进行一次权重的更新。而通过因式分解重新改造后,现在的mini-batch learning的方式,是对同一个query下的所有doc进行一次权重的更新。时间消耗从O(n2)降到了O(n)。这对训练过程的影响是很大的,因为使用的是神经网络模型,每次权重的更新迭代都需要先进行前向预测,再进行误差的后向反馈。
2. Information Retrieval的评价指标
Information Retrieval的评价指标包括:MRR,MAP,ERR,NDCG等。之前的博客中有详细介绍过NDCG和MAP:http://www.cnblogs.com/bentuwuying/p/6681943.html,这里就不再重复介绍了。NDCG和ERR指标的优势在于,它们对doc的相关性划分多个(>2)等级,而MRR和MAP只会对doc的相关性划分2个等级(相关和不相关)。并且,这些指标都包含了doc位置信息(给予靠前位置的doc以较高的权重),这很适合于web search。然而,这些指标的缺点是不平滑、不连续,无法求梯度,如果将这些指标直接作为模型评分的函数的话,是无法直接用梯度下降法进行求解的。
这里简单介绍下ERR(Expected Reciprocal Rank)。ERR是受到cascade model的启发,即一个用户从上到下依次浏览doc,直至他找到一个满意的结果,ERR可以定义为:
其中,表示第i位的doc的相关性概率:
其中,lm表示相关性评分最高的一档。
2.参考
来自:https://www.cnblogs.com/bentuwuying/p/6690836.html
不错的博客:https://blog.csdn.net/u014374284/article/details/49385065