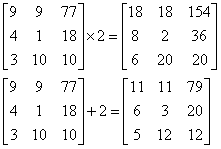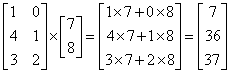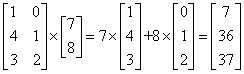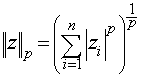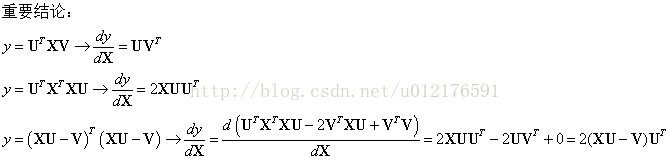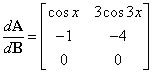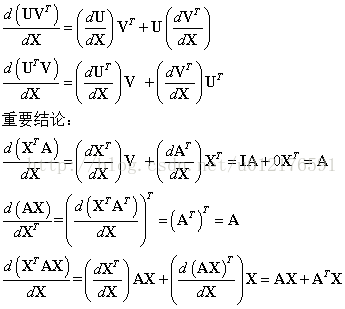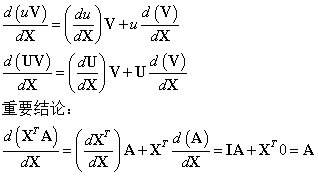自己学习矩阵微分的笔记,包含了迹函数、行列式函数以及逆矩阵的求导方法。
主要是练习求导的链式法则;以及利用微分求导数。
更具体的参见引用:张贤达,矩阵分析与应用,清华大学出版社,2004
Note:向量用加粗的小写字母表示,行向量表示为![]() ,列向量表示为
,列向量表示为![]()
Note:矩阵用加粗的大写字母表示,如![]() ,其转置为
,其转置为![]() 或
或![]()
Note:单位矩阵用![]() 表示,det()表示矩阵的行列式,tr()表示矩阵的迹。
表示,det()表示矩阵的行列式,tr()表示矩阵的迹。
Note:矩阵![]() 和向量
和向量![]() 不依赖于
不依赖于![]() 。
。
参考网站:http://www.psi.toronto.edu/matrix/calculus.html
1.符号说明:
2.矩阵的线性微分(Linear Products)
首先介绍一个重要的性质(类似于函数的求导):
![]()
经验:若d(行向量)/d(列向量)或者d(列向量)/d(行向量),则也适合这个公式,如下面的前两个公式:
![]() 矩阵转置
矩阵转置
图 矩阵的转置过程,转置后行变成列
![]() 用一个数字去加或者乘以矩阵
用一个数字去加或者乘以矩阵
这相当于对矩阵中的每一个元素都独立地进行加法或乘法运算。由于矩阵元素之间的相对值没有发生变化,而只有比例发生了变化,所以上述这类运算称为标量运算(scalar operation)。如果相对矩阵进行常数缩放或者加上一个常数偏移值,就可以使用矩阵标量乘法或加法运算。
图 矩阵上的标量运算,最后的结果是每个元素乘上或者加上某个标量
![]() 两矩阵求和
两矩阵求和
两矩阵要求和,首先必须满足两矩阵的行列数完全一致,矩阵求和相当于每个位置上对应元素求和。
图 矩阵求和
![]() 矩阵乘法
矩阵乘法
两个矩阵要相乘,前一个矩阵的列数必须要等于后一个矩阵的行数。
图 矩阵乘法示意图,
![]()
矩阵相乘还可以看成是列的加权求和。
![]() 矩阵求逆
矩阵求逆
![]()
矩阵要可逆,首先要是方阵,及矩阵的行数等于列数。
方阵也不一定可逆,这时称它奇异(singular)或退化(degenerate)矩阵。如果某个矩阵的某一列可以表示为其它列的线性组合,则该矩阵是奇异矩阵。
如果能够这样表示,则可以把一列的元素全部归于0.
图 一个奇异矩阵的例子。该矩阵有一列为0,意味着该矩阵不可逆。
![]() 向量的范数
向量的范数
范数可以看成向量的长度,可以定义任意阶范数,其形式化定义如下:
可以任意定义自己的向量范数,只要能将向量转换为标量值即可。
![]() 矩阵求导
矩阵求导
1.行向量对元素求导
2.列向量对元素求导
3.矩阵对元素求导
4.元素对行向量求导
5.元素对列向量求导
6.元素对矩阵求导
7.行向量对列向量求导
如果A(一个2*1的向量)要对B(一个3*1的向量)求导,会得到如下3*2的矩阵:
8.列向量对行向量求导
9.行向量对行向量求导、.列向量对列向量求导、矩阵对行向量求导、矩阵对列向量求导、行向量对矩阵求导、列向量对矩阵求导、矩阵对矩阵求导:
计算方式与可以类比于前边的方法,不过区别在于这几个求导得出的结果都是超向量或超矩阵,即它们的元素本身就是向量或矩阵。
10.向量积对列向量求导
11.矩阵积对列向量求导法则
![]()
矩阵求导链式法则的相关用法参见《矩阵运算的若干应用》
http://blog.csdn.net/u012176591/article/details/41552269
http://www.atmos.washington.edu/~dennis/MatrixCalculus.pdf
http://en.wikipedia.org/wiki/Matrix_calculus
http://www.colorado.edu/engineering/cas/courses.d/IFEM.d/IFEM.AppF.d/IFEM.AppF.pdf
http://www.colorado.edu/engineering/cas/courses.d/IFEM.d/
http://select.cs.cmu.edu/class/10725-S10/recitations/r4/Matrix_Calculus_Algebra.pdf
求导公式(撇号为转置):
Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'
乘积的导数
d(f*g)/dx=(df'/dx)g+(dg/dx)f'
于是把以前学过的矩阵求导部分整理一下:
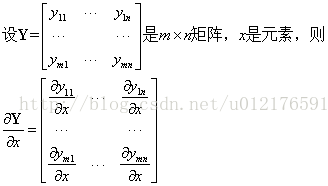
1. 矩阵Y对标量x求导:
相当于每个元素求导数后转置一下,注意M×N矩阵求导后变成N×M了
Y = [y(ij)]--> dY/dx = [dy(ji)/dx]
2. 标量y对列向量X求导:
注意与上面不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量
y = f(x1,x2,..,xn) --> dy/dX= (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'
3. 行向量Y'对列向量X求导:
注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导,将各列构成一个矩阵。
重要结论:
dX'/dX =I
d(AX)'/dX =A'
4. 列向量Y对行向量X’求导:
转化为行向量Y’对列向量X的导数,然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' =(dY'/dX)'
5. 向量积对列向量X求导运算法则:
注意与标量求导有点不同。
d(UV')/dX =(dU/dX)V' + U(dV'/dX)
d(U'V)/dX =(dU'/dX)V + (dV'/dX)U'
重要结论:
d(X'A)/dX =(dX'/dX)A + (dA/dX)X' = IA + 0X' = A
d(AX)/dX' =(d(X'A')/dX)' = (A')' = A
d(X'AX)/dX =(dX'/dX)AX + (d(AX)'/dX)X = AX + A'X
6. 矩阵Y对列向量X求导:
将Y对X的每一个分量求偏导,构成一个超向量。
注意该向量的每一个元素都是一个矩阵。
7. 矩阵积对列向量求导法则:
d(uV)/dX =(du/dX)V + u(dV/dX)
d(UV)/dX =(dU/dX)V + U(dV/dX)
重要结论:
d(X'A)/dX =(dX'/dX)A + X'(dA/dX) = IA + X'0 = A
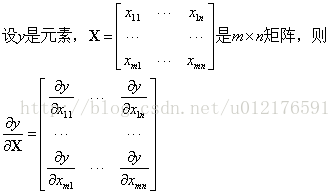
8. 标量y对矩阵X的导数:
类似标量y对列向量X的导数,
把y对每个X的元素求偏导,不用转置。
dy/dX = [Dy/Dx(ij) ]
重要结论:
y = U'XV= ΣΣu(i)x(ij)v(j) 于是 dy/dX = [u(i)v(j)] =UV'
y = U'X'XU 则dy/dX = 2XUU'
y =(XU-V)'(XU-V) 则 dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' +0 = 2(XU-V)U'
9. 矩阵Y对矩阵X的导数:
将Y的每个元素对X求导,然后排在一起形成超级矩阵。
10.乘积的导数
d(f*g)/dx=(df'/dx)g+(dg/dx)f'
结论
d(x'Ax)=(d(x'')/dx)Ax+(d(Ax)/dx)(x'')=Ax+A'x (注意:''是表示两次转置)
矩阵求导 属于 矩阵计算,应该查找 Matrix Calculus 的文献:
http://www.psi.toronto.edu/matrix/intro.html#Intro
http://www.psi.toronto.edu/matrix/calculus.html
http://www.stanford.edu/~dattorro/matrixcalc.pdf
http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf
http://www4.ncsu.edu/~pfackler/MatCalc.pdf
http://center.uvt.nl/staff/magnus/wip12.pdf
汇总自:
http://cherishlc.iteye.com/blog/1765932
http://blog.csdn.net/u012176591/article/details/34251843
http://blog.sina.com.cn/s/blog_4a033b090100pwjq.html