神经网络和深度学习这一块内容与机器学习课程里Week4+5内容差不多。
这篇笔记记录了Week4+5中没有的内容。
参考笔记:深度学习笔记
神经网络和深度学习
- 结构化数据:如数据库里的数据
- 非结构化数据:hard to understand:如图像、文本
一. 深度学习的优势
算法、硬件计算能力的提高使神经网络运行速度变快
大数据(带labels的)使得神经网络精确度更高

在数据集不多的时候深度学习的优势并不是很明显,但是在大数据的情况下,辅助以好的算法和强计算能力,会使神经网络的运行速度和精确度大大提高。
二. Numpy
1. 广播broadcast
两个多维度向量加减乘除时,只要两个向量columns或者ranks有一个相等,即行数相等或者列数相等则可以在相应的位置上进行运算。如果没有哪一个对应相等,则不可以运算。
(m*n)数组 与 (m*1)/(1*n)数组都可以进行+-*/。
运算时(m*1)/(1*n)自动扩充至(m*n)
同理:
(1*m) 与 k也可以运算注意:如果列数等于行数不可以进行运算!唯一的特例:(1,n)与(n,1)之间可以运算,结果为(n,n)维向量
2. 乘法使用
元素乘法:np.multiply(a,b)
矩阵乘法:np.dot(a,b) 或 np.matmul(a,b) 或 a.dot(b)
唯独注意:*,在 np.array 中重载为元素乘法,在 np.matrix 中重载为矩阵乘法!
元素乘法可以用利用broadcast;而矩阵乘法必须要满足(m*n)(n*k)
3. 定义矩阵时的建议
shape: (n,) 与 (1,n) 区别:
例: (4,) [1,2,3,4]
(1,4) [[1,2,3,4]]1.不要使用rank 1array!
如下:
不要使用:
a = np.arange(100)
a = np.random.randn(5)
用(1,n)(n,1)等来代替
a = np.arange(100).reshape(1,100)
a = np.random.randn(1,5)2.经常使用np.reshape来使向量理想化
三. 激活函数
Activation Function:之前神经网络里不同层之间的运算一般都是“加权和+sigmoid函数”。sigmoid函数就是激活函数。还有其他非线性函数可以选择
激活函数大多都是非线性函数:只有输出层可能会有线性函数
以下是四个激活函数:
sigmoid激活函数:除了输出层是一个二分类问题基本不会用它。
tanh激活函数:tanh是非常优秀的,几乎适合所有场合。
ReLu激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用ReLu或者Leaky ReLu。
四. 随机初始化
\(W^{[1]}\)=np.random.randn(2,2)(生成高斯分布),通常再乘上一个小的数,比如0.01,这样把它初始化为很小的随机数。然后\(b^{[1]}\)可以初始化为0。因为只要随机初始化你就有不同的隐含单元计算不同的东西,因此不会有symmetry breaking问题了。相似的,对于\(W^{[2]}\)可以随机初始化,\(b^{[2]}\)可以初始化为0。
五. 深层神经网络
L代表层数,输入层为第0层(l=0)。
一个n层神经网络有n-1层隐藏层((n-1)+1层输出层=n层)
每一层神经网络都有输出,记作\(a^{[l]}\)
输入层输入的特征记作\(x\),但是\(x\)同样也是0层的激活函数,所以\(x=a^{[0]}\)。
最后一层的激活函数,所以\(a^{[L]}\)是等于这个神经网络所预测的输出结果。
六. 矩阵的维度
假设每个样本有\(x\)个特征,训练集总共有m个样本。
\(A^{[l]}\)和\(Z^{[l]}\)维度:(\(n^{[l]}\),m)
\(W^{[l]}\)维度:(\(n^{[l]}\),\(n^{[l-1]}\))
\(b^{[l]}\)维度:(\(n^{[l]}\),1)
无论是前向传播还是反向传播,所有的矩阵维数都是前后一致的!
七. 为什么需要深层神经网络
原因1: 对于深层神经网络,神经网络前几层研究比较低层次的,之后几层是将低层次的内容组合在一起研究复杂层次的。
比如:语音识别:前几层是声音的声波识别->声音的音位->声音里的字母->单词->短语->句子
从最低层次的不断向上提升层次。
原因2: 是遵循电路原理:浅层次的网络相对于深层次的需要指数级的神经单元才能达到和深层次的同样效果。
当然神经网络不是越深越好,层次的深度和调参数一样,也是需要不断的尝试选择一个最适合的层次。
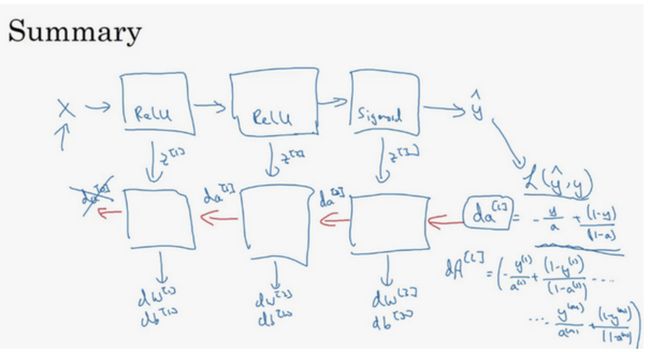
八. 前向传播和反向传播
前向传播公式:
for l in range(1,L+1):
\[ Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]} \]
\[ A^{[l]}=g^{[l]}(Z^{[l]}) \]
其中\(A^{[0]}=X;X={x_1,x_2,x_3}\)
反向传播公式:
认真看这个图: