概率模型
对于概率模型就是由图构成的图模型， 它用观测结点表示观测到的数据，用隐藏的节点表示潜在的信息，而边扮演了描述这些随机结点关系的角色。我们根据图的有向还是无向将有向图成为贝叶斯网络。
说到贝叶斯网络不得不提一个人那就是 托马斯·贝叶斯Thomas Bayes，他曾发表过一篇论文阐述了他的方法-贝叶斯方法，这是一种非常有代表的不确定知识和推理的方法。
我们拿田忌赛马的故事来说，平常人以为每场比赛不是输就是赢，按照概率的计算输和赢各占1/2，但在田忌的眼里不然，由上等马对中等马，由中等马对下等马，则每场赢的概率明显要很大。贝叶斯的思想也是如此，当“样本”固定的情况下，来研究“参数”的变化，这种属于前提性质的分布称为先验分布或者是无条件分布。对于非赢即输的一场比赛，随着人们的经验的积累，对先前条件的观察，人们对胜负的预测已经不是单纯的赢和输，而是更多的对先验条件的考虑。
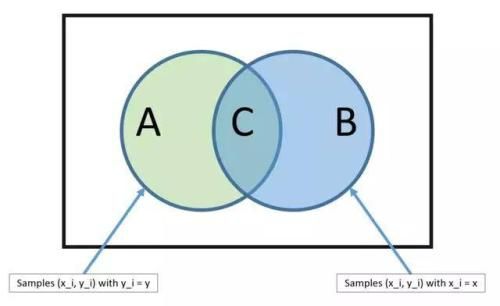
贝叶斯定理：如上图 从B中随机选出元素C 则这个元素在属于B的条件下还属于A的概率为： P(A|B)=P(A∩B)P(B) 其中 P(A|B)是联合概率，P(B)为先验概率。
贝叶斯网络
贝叶斯网络（Bayesian network），又称信念网络（belief network）或是有向无环图模型（directed acyclic graphical model），是一种概率图型模型。其网络拓扑结构是一个有向无环图。
贝叶斯及贝叶斯派提出了一个思考问题的固定模式：
先验分布
+ 样本信息
=后验分布
新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对
的认知是先验分布，在得到新的样本信息后，人们对的认知为。
它们中有因果关系的变量或命题则用箭头来连接，例如 Alarm指向MaryCalls,其中Alarm是MaryCalls的“因（parent）”,反之MaryCalls是Alarm的“果（children）”.其中的条件概率P(M/A)代表Alarm与MaryCalls的链接强度。总之将系统中的随机变量根据是否条件独立绘制在一个有向图里就形成了贝叶斯网络，用来描述随机变量之间的条件依赖，用圈表示随机变量，用箭头表示条件依赖。
而对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：
P(x1,...,xk)=P(xk|x1,...,xk−1)...P(x2|x1)P(x1)
贝叶斯网络的结构形式
1.head to head
即由A B同时指向C 所以有：P(a,b,c) = P(a)P(b)P(c|a,b)成立，即在c未知的条件下，a、b被阻断(blocked)，是独立的。
2.tail to tail
即由c同时指向 A B
考虑c未知和c已知这两种情况：在c未知的时候有：P(a,b,c)=P(c)P(a|c)P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。在c已知的时候，有：P(a,b|c)=P(a,b,c)/P(c)，然后将P(a,b,c)=P(c)P(a|c)P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P(c) = P(c)P(a|c)P(b|c) / P(c) = P(a|c)*P(b|c)，即c已知时，a、b独立。
3.head to tail
即由A指向 C C又指向B C未知时，有：P(a,b,c)=P(a)P(c|a)P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。c已知时，有：P(a,b|c)=P(a,b,c)/P(c)，且根据P(a,c) = P(a)P(c|a) = P(c)P(a|c)，可化简得到：P(a|c)∗P(b|c)，所以在C给定的情况下，a b被阻断。像这种当前状态只跟上一个状态有关，跟其它状态无关的情况，就是一个顺次演变的随机过程，称为马尔科夫链。