二分搜索树又名有序二叉查找树,它有一个特点是左子树的节点值要小于父节点值,右子树的节点值要大于父节点值。基于这样的特点,我们在查找某个节点的时候,可以采取二分查找的思想快速找到这个节点,时间复杂度期望值是为O(log n),但是它有最坏的的情况下。
例如,输入数组[9,7,5,3,1],如果要满足二分搜索树的规则插入一个个节点,这样的二叉树会退化成一条线性表,待会查找元素的时候时间复杂度已达O(N)。
所以针对这种情况,我们引申出了平衡二分搜索树,它每个节点的左右子树高度差不会超过1,它能在O(log n)内完成插入、查找和删除操作。平衡二分搜索树种类比较多,AVL树是其中的一种,但是它是最早被发明的自平衡二分搜索树。
AVL树也会被称为高度平衡树,因为它比二分搜索树多了一个特点:任一节点的左右子树高度差最大为1。如果以后去参赛,可以根据数据的情况更改高度差最大值,甚至也可以制定高度差相差几倍。
计算高度和平衡因子
计算高度是从叶子节点开始的,起始高度默认为1。然后计算叶子节点的父节点高度,比较左右子树的高度,采取最大值再加1就是这个节点的高度了。依此类推,直到整个树的顶点。
计算平衡因子也跟计算高度从叶子节点开始的,然后依次往父节点计算。节点的平衡因子公式是它左子树的高度减去它右子树的高度,有时候也会相反,可负数。
带有平衡因子-1、0或1的节点被认为是平衡的,即期望平衡节点的平衡因子的绝对值不会大于高度差最大值的。带有平衡因子-2或2的节点被认为是不平衡的,意味着需要重新调整这个树。平衡因子的绝对值最大值不会超过高度差最大值+1,说明这个数的任一节点的平衡因子不会出现-3或3。
如果改定高度差最大值为2,那么平衡因子会出现-3或3了,同时这个节点也是不平衡的,需要旋转调整。带有平衡因子-2、-1、0、1或2则被认为是平衡的。
动画
算法动画视频地址
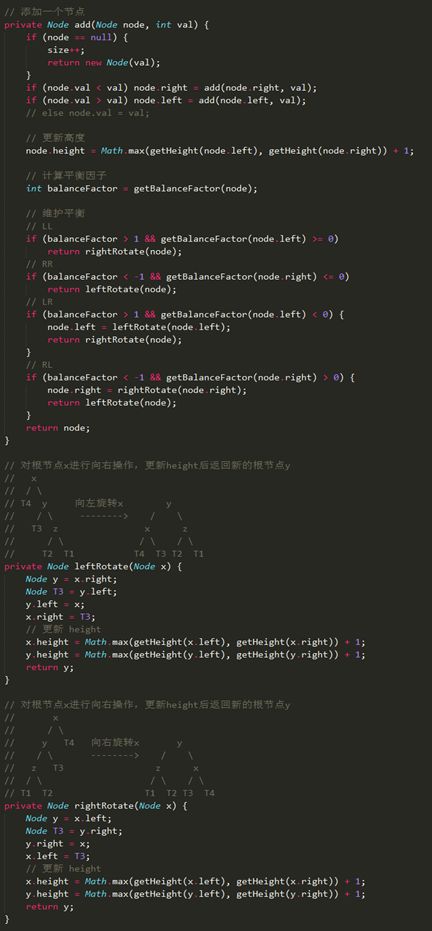
Code
左旋转和右旋转
AVL树调整不平衡的节点分为左旋转和右旋转,却分四种情况:LL、RR、LR和RL。其中L是左旋转,R是右旋转。如何采取使用哪一种情况则看插入的节点在哪里。
如果插入的节点是再T2子树里面,T1、T2、T3和T4都代表一个子树。T2里面插入一个节点,这个子树的高度加1,再计算父节点的平衡因子。如果这个节点是平衡的,则更新这个节点的高度。然后再往上计算父节点的平衡因子,接着判断是否平衡,如果是平衡的则更新高度,直到是不平衡的则进行旋转操作。
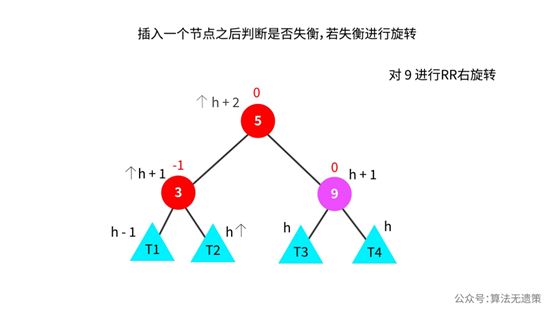
看上面图中,节点9是不平衡的,需要进行旋转操作。那如何进行哪种情况操作呢?
看左右子树哪一个子树插入了一个节点,节点5的左子树高度加1,导致节点5的平衡因子由0变成1。为了让节点5的平衡因子可以由1变成0,则希望节点5的右子树可以高度加1,所以就向节点5的父节点9进行右旋转操作,重新调整平衡因子,节点5的平衡因子恢复为0。
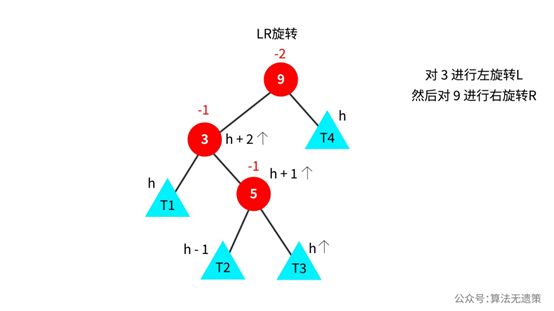
如果是下面情况,则不能单纯的进行右旋转操作了。看下面途中,插入一个节点是在节点3右子树发生的,节点3的平衡因子由0变成-1,应该希望是节点3左子树的高度可以高点。所以对节点3进行左旋转操作。
对节点3进行左旋转操作之后,更新相应节点的高度和平衡因子。看下面图中,发现节点5的平衡因子由-1变成1了,为了让1变成0,则希望是节点5的右子树高度可以高一点,所以对节点9进行右旋转操作。
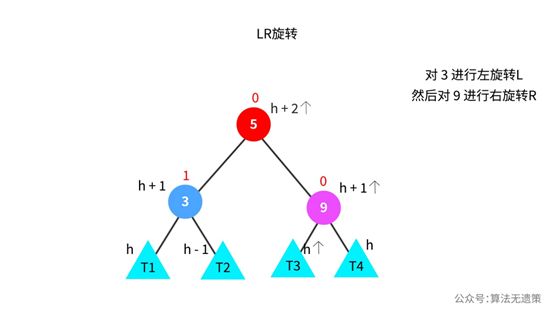
进行LR旋转的操作如下图,节点5的平衡因子已恢复为0,节点9由开始的不平衡已变成平衡。
动画
算法动画视频地址
Code
删除节点
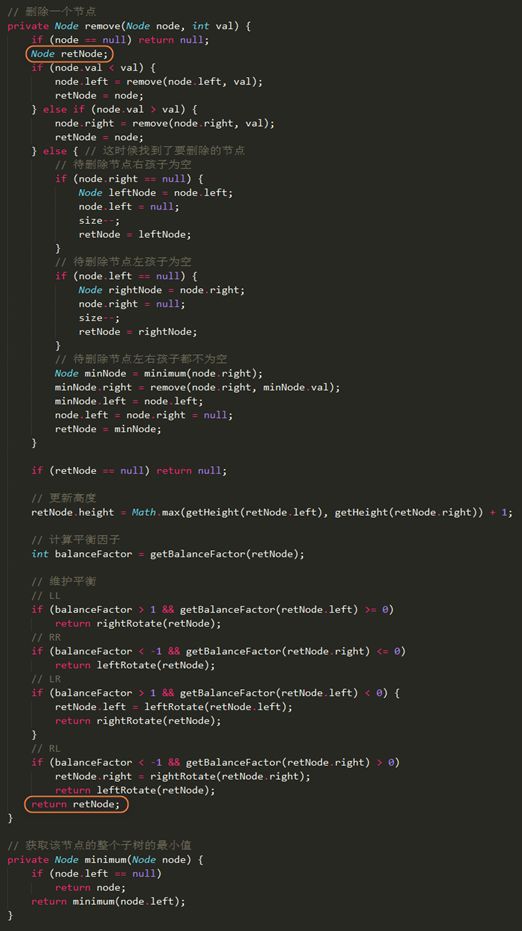
AVL树的删除操作和二分搜索树一样,也分待删除结点的右子树为空、左子树为空和左右子树都不为空的情况。
那如何更新高度和平衡因子,不平衡的节点又如何调整为平衡的呢?和插入节点一样。
插入节点是插入一个节点后从叶子节点计算高度,然后再到父节点根据左右子树的高度计算平衡因子,接着更新高度,再到上一个父节点,直到整个二叉树的顶点。
删除节点可以看作是包含插入节点的,因为删除一个节点后会从左右子树中拉上来一个节点,不会再从叶子节点从新计算高度了,而是从左右子树开始接着更新高度和计算平衡因子。
动画
算法动画视频地址
Code
长按下图二维码关注公众号,「算法无遗策」持续更新算法