神经图灵机 Neural Turing Machine-DeepMind

Neil Zhu，ID Not_GOD，University AI 创始人 & Chief Scientist，致力于推进世界人工智能化进程。制定并实施 UAI 中长期增长战略和目标，带领团队快速成长为人工智能领域最专业的力量。
作为行业领导者，他和UAI一起在2014年创建了TASA（中国最早的人工智能社团）, DL Center（深度学习知识中心全球价值网络），AI growth（行业智库培训）等，为中国的人工智能人才建设输送了大量的血液和养分。此外，他还参与或者举办过各类国际性的人工智能峰会和活动，产生了巨大的影响力，书写了60万字的人工智能精品技术内容，生产翻译了全球第一本深度学习入门书《神经网络与深度学习》，生产的内容被大量的专业垂直公众号和媒体转载与连载。曾经受邀为国内顶尖大学制定人工智能学习规划和教授人工智能前沿课程，均受学生和老师好评。

作者:
Alex Graves [email protected]
Greg Wayne [email protected]
Ivo Danihelka [email protected]
Google DeepMind, London, UK

原文：http://arxiv.org/pdf/1410.5401.pdf

gitbook 链接

悠长的历史会让人迷失在巨大的信息中，所以直接从第三节开始给出神经图灵机的介绍、解释和实验分析。

3 神经图灵机

神经图灵机包含两个基本组成部分：神经网络控制器和记忆库。

神经图灵机

控制器通过输入输出向量和外界交互。不同于标准神经网络的是，控制器还会使用选择性的读写操作和记忆矩阵进行交互。类比于图灵机，我们将网络的参数化这些操作的输出称为“读头”。
最关键的是，每个组成部分都是可微的，这样可以更加直接地使用梯度下降进行训练。我们通过定义�模糊的读写操作根据一个更高或者更低的度（degree）和的记忆中的所有元素进行交互（而不是像在正常的图灵机或者数字计算机那样一次只是处理一个单个的元素）。这个模糊的度由一种注意力聚焦机制确定，将每个读写操作限制在记忆中的一小块上，忽略其他部分。因为和记忆的交互是高度稀疏的，NTM 倾向于无干扰地存储数据。进入注意力聚焦的记忆位置由读头特定的输出确定。这些输出定义了一个规范化的权重在记忆矩阵的行上（对应于内存位置）。每个权重，对应于一个读头或者写头，定义了在每个位置读写的程度。读头可以在单个位置相当重视或者分散精力在若干位置。

3.1读

令 $$M_t$$ 为 $$N\times M$$ 在时间 $$t$$ 的记忆矩阵，其中 $$N$$ 是记忆位置的数目，而 $$M$$ 是每个位置的向量的大小。令 $$\mathbf{w}_t$$ 是在时间 t 一个读头输出的在 N 个位置上的向量。因为所有权重都是规范化的，$$\mathbf{w}_t$$ 的 N 个元素 $$w_t(i)$$ 遵循下面的限制：

由读头返回的长度为 $$M$$ 的读向量 $$r_t$$ 定义成一个记忆中行向量 $$M_t(i)$$ 凸包:

这显然是对记忆和权重都是可微的。

3.2 写

受到 LSTM 中的输入和忘记门的启发，我们将每个写操作分解成了两个部分：消除和添加：erase + add。

给定在时间 t 写头输出的权重 w_t，跟上一个消除向量 e_t 其中 M 个元素都是在 (0,1) 之内的，来自前一个时间步记忆向量 M_{t-1}(i) 做出如下修改：

其中 $$\mathbf{1}$$ 是元素都是 $$1$$ 的行向量，按点进行每个记忆位置的乘法。因此，记忆位置的元素重置为 0 如果在位置处的权重和消除元素都是 1；如果两个中有一个为 0，记忆就保持不变。当多个写头给出了，消除操作可以按照任意的顺序进行，因为乘法实际上是可交换的。

每个写头同样还会产生一个长度为 M 的加法向量 a_t，这个会在每个消除步执行后被加到记忆中：

另外，多个头进行的加法操作的顺序是不相关的。所有写头上的消除和添加操作产生了在时间 $$t$$ 最终的记忆内容。由于消除和添加操作都是可微的，符合写操作就也是可微的了。注意到，消除和添加向量有 $$M$$ 个独立的部分，这样可以更好地控制在每个内存位置上的那些需要修改的元素。

3.3 寻址机制

尽管我们已经展示了读写操作的方程，还没有描述权重如何产生。这些权重是通过合并两个寻址机制产生的。第一个机制，“基于内容的寻址”，将注意力集中在基于当前值和控制器产生的值之间的相似度来确定的位置上。这和 Hopfiled 网络的基于内容寻址方式是相似的。（Hopfield 1982）这样的好处是检索变得简单，仅仅需要控制器去产生存储数据的部分的近似，然后这个值会和内存进行比较从而产生准确的存储值。

然而，不是所有的问题都是适合基于内容的寻址的。在某些任务中，变量的内容是任意的，但是变量仍然需要可识别的名称或者地址。算术问题就属于这一类：变量 $$x$$ 和变量 $$y$$ 可以用两个值作为输入，但是过程 $$f(x,y) = x \times y$$ 仍然需要定义。对该任务的控制值需要以 $$x$$ 和 $$y$$ 作为输入，将他们存放在不同的地址中，然后对他们进行检索，并执行乘法算法。这种情形下，变量通过地址进行检索，而不是内容。我们将这种类型的寻址称为“基于地址的寻址”。基于内容的寻址严格上比基于地址的寻址更加一般，因为内存地址中的内容可以包含地址的信息。不过在我们的实验中，提供基于地址的寻址作为原语曹组可以对某些形式的泛化更加有效（essential），所以我们将两种机制同时采用了。

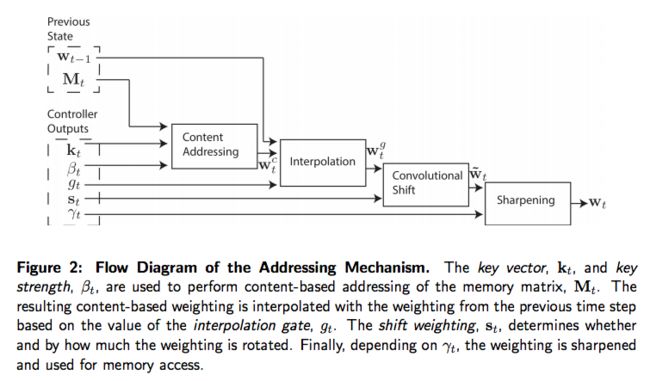
图 2 展示了整个寻址系统的流程图，包含了在读或者写的时候构造一个权重向量的操作的顺序。

图 2

3.3.1 通过内容聚焦

对基于内容寻址，每个读头（用在读或者写上）首先会产生一个长度为 M 的 key vector $$k_t$$，这个会和每个向量 $$M_t(i)$$ 通过相似性度量 $$K[\dot,\dot]$$ 进行比较。基于内容的系统产生了一个正规化的权重 $$w_t^c$$ 基于相似度和正的 key strength $$\beta_t$$，这个可以扩大或者减少聚焦（focus）的准确度：

在我们现在的实现中，相似性度量就是余弦相似度：

3.3.2 通过位置聚焦

基于位置的寻址机制为了利用在内存的空间上进行简单的迭代和随机访问跳跃的好处。这是通过一个权重的旋转变换来实现的。例如，如果当前权重聚焦在一个单个位置上，$$1$$ 的旋转将会聚焦到下一个位置。而一个负的变换则会将权重聚焦到相反的方向上。

在旋转前，每个读头产生一个标量的 interpolation gate $$g_t$$，其值在 $$(0,1)$$ 内。$$g$$ 的值被用来在前一个时间步读头产出的权重 $$w_{t-1}$$ 和在当前时间步内容系统的产出的权重 $$w_t^c$$ 之间进行合成（blend）得到 gated weighting $$w_t^g$$：

如果这个 gate 是 $$0$$，那么内容权重就整个被忽略了，就会使用前一时间步的权重。相反，如果 gate 是 $$1$$，来自前一步的权重就完全被忽略了，整个系统就使用了基于内容的寻址。

在 interpolation 之后，每个读头产生一个 shifting 权重 $$s_t$$，在所有允许的整数偏移上的定义了一个正规化的分布。例如，如果在 $$-1$$ 到 $$1$$ 之间的 shifting 权重被允许，$$s_t$$ 就有是哪个元素对应于偏移的程度 $$-1$$，$$0$$ 和 $$1$$。定义偏移权重的最简单的方式就是使用一个在跟控制器相关的合适大小 softmax 层。我们还实验了另一种技术，其中控制器产生一个单个标量被解释为一个在偏移上的均匀分布的宽度下界。例如，如果偏移变量是 $$6.7$$，那么 $$s_t(6) = 0.3$$，$$s_t(7) = 0.7$$，剩下的就是 $$s_t = 0$$。

如果我们将 $$N$$ 个内存位置索引为 $$0$$ 到 $$N-1$$，那么通过 s_t 应用在 w_t^g 上的选择可以按照下面的 circular 卷积表示：

其中所有的索引算术都是进行了模 $$N$$ 处理。在偏移权重不很平缓时，卷积操作可能会随时间产生权重的丢失或者发散（leakage or dispersion）例如，如果偏移 -1 0 1 给定了权重 0.1 0.8 0.1，那么旋转将会转换权重聚焦在一个单一的点变成三个点上的模糊不清。为了避免这个情况，每个读头产生一个另一个标量 $$\gamma_t\geq 1$$，其作用就是将最终的权重变得更加的陡峭：

权重 interpolation 和基于内容及地址机制合并的寻址系统可以以三种互补方式执行。第一，权重可以通过内容系统选出而不需要位置系统的支持。第二，通过内容寻址系统产生的权重可以被选择然后进行偏移。这使得聚焦可以跳到紧邻的下一个位置，但是不能够跳到由内容获取的位置；用计算机科学术语就是这允许读头找到连续的数据块，并在这个块中获取一个特定的元素。第三，来自前一个时间步的权重可以不用任何基于内容寻址系统的输入进行旋转。这可以让权重可以通过一系列的寻址在每个时间步增加同样的距离进行。

3.4 控制器网络

上面描述的神经图灵机架构有几个自由参数，包括内存的大小，读写头的数量和允许的位置偏移的范围。但是可能表现最好的选择是将神经网络作为控制器。特别地，我们需要确定是否使用一个循环或者前驱神经网络。诸如 LSTM 这样的循环控制器有其本身的内存，可以作为矩阵中更大的内存的补充。如果我们将此控制器和计算机的中央处理器，将内存矩阵和 RAM 进行对比，那么循环神经网络的控制器的隐藏层激活就和处理器重的多个时间步相关了。他们可以用控制器来混合多个时间步的信息。另一方面，前驱控制器可以通过在每一步内存中进行读写模仿一个循环网络。甚至，前驱控制器常常能给出更大的网络操作的透明度，因为从内存矩阵中读出和写入到内存矩阵通常比一个循环神经网络的内部状态更容易解释。然而，前驱控制器的一个缺点就是并发读和写头会产生NTM的计算瓶颈。使用单一的读头，就只能执行一个在每个时间步对单个的内存向量进行一元变换，两个读头则可以进行双向量变换，如此类推。循环控制器可以内部存储前一个时间步的读向量，所以不会受到这个的限制。

4. 实验

本节给出一些基本的实验，在一些简单算法任务上，例如数据的复制和排序。不仅仅是为了展示 NTM 能够解决这些问题，而且说明了 NTM 能够通过学习紧致的内部程序。这些解决方案的特点是他们可以超越训练数据的界限。例如，我们很好奇如果一个网络已经学会了复制 20 长度的序列，是不是它就可以复制长度 100 的序列，而不需要额外的训练。

对所有的实验，我们比较了三个架构：使用前驱控制器的 NTM，LSTM 控制器的 NTM 和标准的 LSTM 网络。因为所有任务都是按阶段的，我们就在每个输入序列的开始重置了网络的动态状态。对 LSTM 网络，这种设置下前一时间步的隐藏状态就是一个学到的偏差向量。对 NTM 控制器的前一个状态，前一阶段读出的向量，和内存的内容都会重设置为偏差值。所有这些任务都是监督学习问题，其目标是二元的；所有网络都是 logistic sigmoid 输出层并且使用了 cross-entropy 目标函数训练。序列预测误差按照 bits-per-sequence 进行汇报。更多细节参见 4.6 节的实验参数。

4.1 复制

复制任务测试 NTM 是否能够存储和复现一个任意信息的长序列。网络会用随机二元向量作为输入序列，并跟上一个分隔符。对长期时间段的信息的存储和获取是循环神经网络和其他一些动态架构的弱项。我们特别想知道 NTM 是不是能够比 LSTM 更好地衔接更长的时间间隔。

网络训练复制 8 个bit 的随机向量，其中序列长度是 1 到 20 之间随机值。目标序列简单就是输入序列的副本（不含有分隔符）注意在网络接收到目标时，并没有输入给网络，这样保证它可以不要任何帮助回忆起整个序列。

正如在图 3 中展示的那样，NTM（用前驱或者 LSTM 控制器）比单单的 LSTM 学得更快，并且收敛到一个更低的代价上。而 NTM 和 LSTM 学习曲线之间的明显差距也给出了一个可以定性分析两个模型解决这个问题方式的不同。

图 4

图 5

我们同样研究了这些网络泛化到更长序列的能力。图 4 和图 5 展示了 LSTM 和 NTM 在这个设置下的行为差异巨大。NTM 在长度增加时还能够复制，不过 LSTM 在超过 20 长度后迅速变差。

图 6

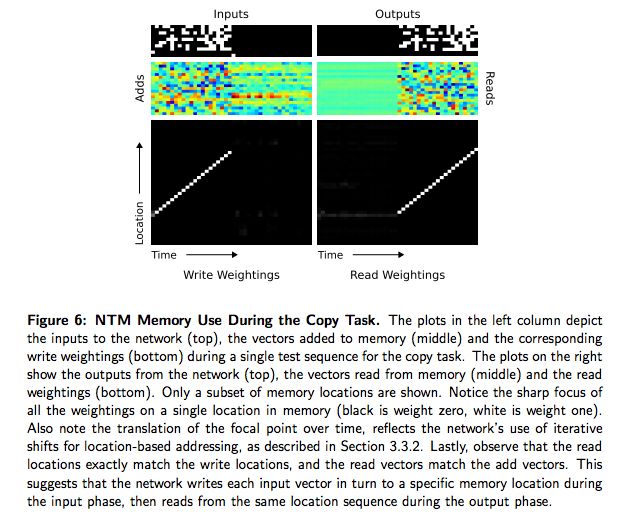
前面的分析说明和 LSTM 不同 NTM它已经学到某种形式的复制算法。为了确定这种算法是怎么样的，我们检查了控制器和内存之间的交互，见图 6。我们相信操作序列可以被下列伪代码总结：

initialise: move head to start location

while input delimiter not seen do

• receive input vector
• write input to head location
• increment head location by 1

end while
return head to start location

while true do

• read output vector from head location
• emit output
  *increment head location by 1

end while

这实际上就是一个人类程序员在低级程序设计语言上执行同样任务的方式。用数据结构的术语看，我们可以说 NTM 已经学会了如何创建和数据迭代。注意算法合并了基于内容的寻址（跳到序列的开始）和基于位置的寻址（在序列上进行移动）。同样要注意不增加从前一个读写权重相对偏移的能力迭代可能不会推广到长的序列（公式 7） 以及不使用聚焦增陡（sharpening）机制（公式 9）权重可能就随时间丢失精度了。

4.2 重复复制

重复复制任务以输出复制的序列指定次数并输出一个序列终止符作为复制任务的扩展。我们进行这个实验的动机是想看看 NTM 是否可以学习一个嵌套的函数。理想目标是，我们希望它可以执行一个 for 循环，包含任意已经学到的子过程。

网络接受了随机长度的随机二元向量序列，跟随一个标量值表示复制的次数，使用一个分开的输入信道进行。为了在正确的时间输出终止标志网络必须能够解释额外的的输入并保存已经进行过了的复制次数。和复制任务类似，在初始化序列和复制数目之后并没有其他输入给网络。网络训练的目标是重新产生长度为 $$8$$ 的随机二元向量，其中序列长度和复制次数都是从 $$1$$ 到 $$10$$ 之间随机选择的。代表重复次数的输入被正规化为均值为 $$0$$ 方差为 $$1$$。

图 7

图 8

图 9

图 7 展示了 NTM比 LSTM 在这个任务上学习得更快，但是都是能够很好地解决这个问题。其中这两个架构的差异就是在让进行更加泛化的任务时变得明显了。我们这里考量了两个维度的泛化：序列长度和重复数目。图 8 分别对 NTM 和 LSTM 解释了前者 2 倍的效果及后后者 2 倍的效果。LSTM 在这两种情形下都出问题了，NTM 对更长的序列也是有效的，并且可以执行超过 10 次的重复；不过 NTM 不能够保持自己已经完成了多少次重复，没有能够正确预测正确的终止符。这可能是数值表示重复次数的后果，因为这样不能够轻易地进行超过一个固定长度的泛化。

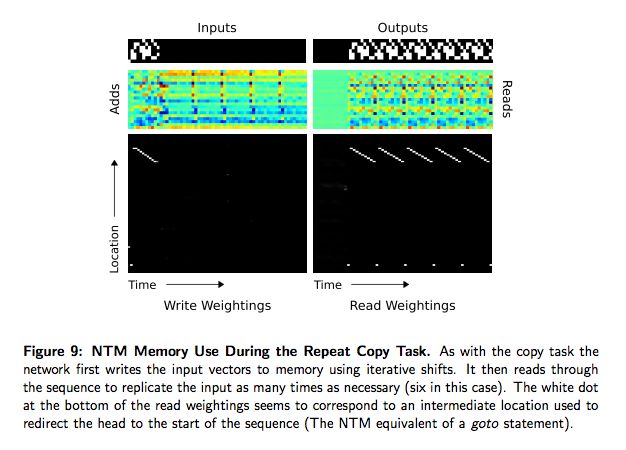
图 9 给出了 NTM 学到一个在前一节中复制算法的简单扩展，其中序列化读取重复了足够多次。

4.3 关联回忆

前面的任务展示了 NTM可以应用算法到相对简单、线性数据结构上。下一个复杂性就出现在带有指针的数据结构上——其中的项指向另一个。我们测试了 NTM 学习这类更加有趣的结构的实例上，通过构造一个项目的列表是的查询其中一个项目需要网络返回后续的项目。更加细节地说，我们定义一个项目作为二元向量的序列，通过左右终止符来进行限制。在几个项目已经被传递给网络后，我们通过展示一个随机的项目进行查询，我们让网络产生这个项目后面的一个。在我们的实验中，每个项目包含三个 6 bit 的二元向量（总共就是 18 bit 每项目）。在训练的时候，我们使用最小 2 项目和最大 6 个项目在每个阶段（episode）。

图 10

图 11

图 10 展示了 NTM 比 LSTM 学习的速度明显快很多，在接近 30,000 episode 的时候接近 0 的代价，而 LSTM 并没有在 100 万 episode 后达到 0 的代价。另外，采用前驱控制器的 NTM 比使用 LSTM 控制器的 NTM 学习的速度更加快。这两个结果表明 NTM 的外存的确是比 LSTM 的内部内存更加有效的一种维持数据结构的方式。NTM 同样比 LSTM 在更加长的序列上泛化得更好，可以在图 11 中看到。使用前驱控制器的 NTM 对 接近 12个项目的情形下接近完美的效果（两倍于训练数据的最大长度），仍然有低于 15 个项目的序列每序列 1 bit 的平均代价。

图 12

在图 12 中，我们展示了在一个单个测试 episode 通过一个 LSTM 控制读头的 NTM 内存操作。在“�Inputs”中，我们看到输入代表项目的分隔符在第 7 行作为单一的 bit。在项目的序列已经进行传递后，在第 8 行的一个分隔符让网络准备接受一个查询项目。这里，查询项目对应于在序列中（在绿色盒子中）的第二个项目。在“�Outputs”中，我们看到了网络给出了输出在训练中的项目 3 （在红色盒子中）。在“读取权重”中，在最后三个时间步，我们看到控制器从连续位置上读取了项目 3 的时间分片。这非常奇怪，因为这看起来网络已经直接跳到了正确的存储项目 3 的位置。然而，我们可以解释这个行为通过看“写权重”。这里我们发现，内存甚至在输入给出了一个分隔符的时候进行了写操作。我们可以在“Add”确认这个数据实际上在给定分隔符的时候已经写入内存（比如，在黑色盒子中的数据）；而且，每次分隔符出现，加入到内存中的向量是不同的。更多的分析揭示出网络在通过使用基于内容的查找获得了器读取后相应的位置移动一位的位置。另外，使用内容查找的 key 对应于添加到这个黑色盒子的向量。这其实表示了下面的算法：在每个项目分隔符给出的时候，控制器写一个该项目的前三个时间片压缩的表示。在查询过来时，控制器重新计算同样的查询的压缩表示，使用基于内容的查找来获得第一次写表示的位置，然后偏移 1 位来产生后续的序列中的项目（这样就把基于内容的查找和基于位置的偏移结合起来了）。

4.4 动态 N-Grams

动态 N-Grams 任务的目标就是测试 NTM 是否可以快速适应新的预测分布。特别地，我们对 NTM 是否能使用其内存作为一个重写的表，可以用来保存变换统计的数量，因此来衡量传统的 N-Gram 模型。
我们考虑所有可能的在二元序列上的 6-Gram 分布。每 6-Gram 分布可以被表示成一个 $$2^5 = 32$$ 个数字的表，表示了在给定所有可能的长度为 5 的二元历史序列时下一个 bit 为 1 的概率。对每个训练样本，我们首先通过独立地从 $$Beta(\frac{1}{2},\frac{1}{2})$$ 中采样所有 32 个概率产生随机的 6-Gram 的概率。

我们然后使用当前的查找表通过采样 200 个按 bit 顺序产生的特殊的训练序列。这个网络一次看序列的一个 bit，然后被询问预测下一个 bit。这个问题的最有预测器可以通过贝叶斯分析（Murphy，2012）获得：

图 13

其中 $$c$$ 是在前面的上下文中的 5 个bit，$$B$$ 则是下一个 bit 的值，而 $$N_0$$ 和 $$N_1$$ 在序列中目前为止�对应于 0 和 1 的次数。因此，我们可以将 NTM 和 LSTM 进行对比。为了衡量性能，我们使用了一个从 1000 个 长度为 200 的序列，从和训练数据同样的分布中采样出来的。如图 13 所示，NTM 获得了小的但是显著地性能提升，但是并没有达到最优的代价。这两种架构在观察到新的输入时的进化在图 14 中进行了展示，并加上最优预测进行比对。NTM 内存使用情况的分析（图 15）表明控制器使用内存来计算有多少个 1 和 0，已经在不同的上下文中看到了，这样使得能够实现类似于最优估计的算法。

图 14

图 15

4.5 优先级排序

图 16

这个任务测试 NTM 是否能对数据进行排序——重要的基本算法。随机二元序列向量的序列跟随一个标量的优先级作为网络的输入。优先级是从 $$[-1,1]$$ 之间进行均匀采样的。木i包含根据优先级进行排序后的二元向量，如图 16 所示。

图 17

每个输入序列包含 20 个二元向量，及对应的优先级，每个目标序列是输入中 $$16$$ 个最高优先级向量。NTM 的内存使用情况检查让我们得出一个假设，它使用优先级来确定每次写得相对位置。为了检测这个假设，我们拟合了一个优先级线性函数到观测的写位置。图 17 展示了由这个线性函数紧紧的匹配的观测到得些位置。同样还展示了网络从内存位置中读出是按照递增顺序，就是对排序的序列进行遍历。

图 18

图 18 中的学习曲线展示了使用了前驱控制器和 LSTM 控制器的 NTM 从本质上在这个任务上超过了 LSTM。注意到 8 个并行的读和写头需要用来在次任务上拥有最优的性能；这可能会反映出仅仅使用一元的向量操作就能够对向量进行排序的难度。

4.6 实验细节

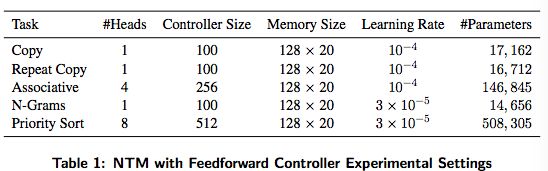
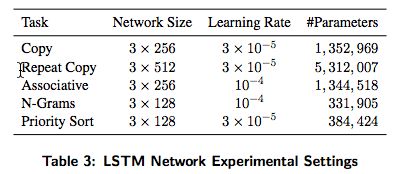
对所有的实验，RMSProp 算法用来进行训练，按照 Graves 2013 的研究形式并以 momentum 为 $$0.9$$。表 1 到 3 给出了网络配置和学习率的细节。所有的 LSTM 网络有三个 stacked 隐藏层。注意 LSTM 参数的数量随着隐藏元的个数以平方增长（由于递归链接的缘故）。这个和 NTM 不同，其中参数的数量并不会随着内存位置的数量而增加。在反向传播训练中，所有的梯度部分都限制在 $$(-10,10)$$ 之间。

表 1

表 2

表 3

5 总结

我们介绍了 NTM，一种从生物可行内存和数字计算机的启发产生的神经网络架构。如同传统的神经网络，这个架构也是可微的端对端的并且可以通过梯度下降进行训练。我们的实验展示了它有能力从样本数据中学习简单的算法并且能够将这些算法推广到更多的超越了训练样本本身的数据上。

6 致谢

Many have offered thoughtful insights, but we would especially like to thank Daan Wierstra,
Peter Dayan, Ilya Sutskever, Charles Blundell, Joel Veness, Koray Kavukcuoglu,
Dharshan Kumaran, Georg Ostrovski, Chris Summerfield, Jeff Dean, Geoffrey Hinton, and
Demis Hassabis