1. 基本计数的母函数
现在来用母函数来求解基本计数问题,母函数既可以完成自动计数,还能表示计数本身,像Stirling数这种就只能用母函数表示。自动计数适用于可以分步的计数问题,并且目标值是每步值之和,这与多项式的运算性质有关。
1.1 组合数和分划数
直观上最符合这一特点的就是模型2,从\(n\)个可区别对象中选出\(m个\)。限制第\(k\)个对象被取的次数在集合\(M_k\)中,它被选情况的母函数是\(\sum\limits_{i\in M_k}x^i\),所有元素被选择的情况可以借助母函数(1)自动计数,共选取\(m\)个元素的个数是\(x^m\)的系数。特别地,不可重复组合数的母函数是\((1+x)^n\),可重复组合数的母函数是\(\dfrac{1}{(1-x)^n}\)(注意\(1+x+x^2+\cdots=\dfrac{1}{1-x}\)),满射的母函数是\(\dfrac{x^n}{(1-x)^n}\)。
\[\sum_{k=0}^{\infty}c_kx^k=\prod_{i=1}^n\left(\sum_{j\in M_i}x^j\right)\tag{1}\]
对于模型4的分拆数,考虑到\(1^{\lambda_1}2^{\lambda_2}\cdots m^{\lambda_m}\)型分拆要满足上篇式(14),它也可以用母函数自动计数。对长度为\(k\)的分部使用\(x^{k\lambda_k}\),故长度为\(k\)的分部的母函数是\(1+x^k+x^{2k}+\cdots=\dfrac{1}{1-x^k}\)。所以\(p(m)\)的母函数便是式(2),由于\(p(m,k)\)等于最大分部为\(k\)的分拆数,故它的母函数是式(3)。
\[\sum_{n=0}^{\infty}p(n)x^n=\prod_{i=1}^{\infty}(1-x^i)^{-1}\tag{2}\]
\[\sum_{n=0}^{\infty}p(n,k)x^n=x^k\prod_{i=1}^k(1-x^i)^{-1}\tag{3}\]
值得一提的是,欧拉当初就是在研究分划数时发现母函数方法的。即使有式(2),\(p(m)\)的性质还是不清楚,我们注意到(2)的逆\(q(x)\)相对比较简单,值得讨论一下。\(q(x)\)有一个还算显然的组合意义,每一项系数的绝对值是分部互异的分划数,符号的意义则是分部数为奇数和偶数时分划数的差。利用这一组合意义辅助讨论(过程见教材),不难得到\(q(m)\)满足式(4)。继而可得到\(p(m)\)的递推关系式(5),它被称为欧拉公式。
\[q(m)=\left\{\begin{matrix}(-1)^k,&\text{if}\;m=\frac{1}{2}(3k^2\pm k)\\0,&\text{if}\;m\ne\frac{1}{2}(3k^2\pm k)\end{matrix}\right.\tag{4}\]
\[p(m)=\sum_{k=1}^{\infty}(-1)^{k-1}\left(p(m-\frac{3k^2-k}{2})+p(m-\frac{3k^2+k}{2})\right)\tag{5}\]
• 利用母函数证明:分部都为奇数的分划数等于分部互异的分划数。
1.2 指数型母函数
对于模型1的排列数,简单的相加显然不再满足,考察上篇式(2),这就启发我们用\(\dfrac{x^k}{k!}\)代替\(x^k\)(式(6))。对于数列\(c_n\),级数(6)被称为数列的指数型母函数,它对排列问题非常适用。同上面的分析,\(n\)个互异元素中选\(m\)个排列的母函数是式(7)。特别地,无重复排列数的母函数是\((1+x)^n\),可重复排列数的母函数是\(e^{nx}\)(注意\(1+x+\dfrac{x^2}{2!}+\cdots=e^x\)),满射排列数的母函数则是\((e^x-1)^n\)。
\[\sum_{k=0}^{\infty}c_k\dfrac{x^k}{k!}=c_0+c_1\dfrac{x}{1!}+c_2\dfrac{x^2}{2!}+c_3\dfrac{x^3}{3!}\cdots\tag{6}\]
\[\sum_{k=0}^{\infty}c_k\dfrac{x^k}{k!}=\prod_{i=1}^n\left(\sum_{j\in M_i}\dfrac{x^j}{j!}\right)\tag{7}\]
最后趁热看一下模型3中的Stirling数,由于\(k!S(m,k)\)就是模型1中的满射,利用满射排列数的母函数容易知\(S(m,k)\)的指数型母函数(式(8)),利用指数型母函数也可以得到上篇式(26)。为了得到\(s(m,k)\)的指数型母函数\(g_k(x)\),从上篇式(27)右得到启发,先计算\(g_k(x)\)的母函数得到\((1+x)^y\)(过程略,二层母函数使用\(y\)),展开\(y\)的幂级数便得到\(s(m,k)\)的指数型母函数(9)。有了指数型母函数,Stirling数的性质就可以通过母函数研究,比如对母函数求导能得到递推关系式(10)(11)。
\[\sum_{m=0}^{\infty}S(m,k)\dfrac{x^m}{m!}=\dfrac{1}{k!}(e^x-1)^k\tag{8}\]
\[\sum_{m=0}^{\infty}s(m,k)\dfrac{x^m}{m!}=\dfrac{1}{k!}(\ln(1-x))^k\tag{9}\]
\[S(m,k)=\sum_{i=k-1}^{m-1} \binom{m-1}{i}S(i,k-1)\tag{10}\]
\[s(m,k)=\sum_{i=k-1}^{m-1}(-1)^{m-i-1}(m-1)_{m-i-1}s(i,k-1)\tag{11}\]
• 求每个元素取到偶数个的排列数。
2. Pólya计数定理
2.1 引言和环状字
基本计数问题中只涉及了两个最极端的拓扑结构,但在阐述的过程中,我们一直强调了同构类的思想。这里将推广这个思想,并将其用到更多的拓扑结构中。所谓同构,就是将拓扑结构中的元素置换,元素间的关系和置换后一致,它的代数意义就是我们熟悉的\((a,b)=(f(a),g(a))\)。我们这里就不再说元素可区分、不可区分了,每个元素单独看都无差别,它的差异性完全由其在拓扑结构中的位置决定。
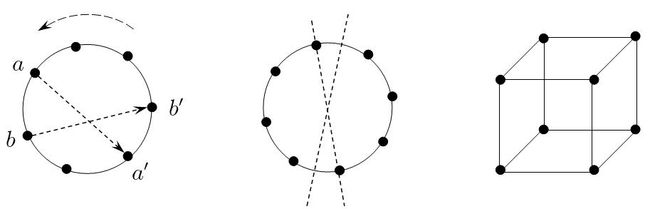
比如图中的环状拓扑,直觉上说每个元素是“不可区分”的,但它们却不能随便置换。当把\(a\)置换到\(a'\)时,为了保持\(a,b\)的关系,\(b\)只能置换到\(b'\),所以这个拓扑中的同构就只能是整个图的旋转。再来看另一个环状拓扑,它除了旋转之外,延虚线的翻转也是同构置换。最后的立方体,其中包括更多同构置换,它们都与我们的直觉对应,就是变动后仍与以前一样。为了简单起见,以下我们只讨论原像是复杂拓扑,而像是可区分集的问题。它的等价模型就是给拓扑结构的元素染色,这时的同构当然还要求元素被置换到同样颜色的元素。
如果原像是左图的\(m\)阶有向环形,用\(n\)种颜色为其染色(或写入\(n\)种字母),结果被称为\(m\)元环状字,同构环状字的个数记作\(C_n(m)\)。先将环形固定并对其染色,将环状字进行旋转,得到的不同染色方案便是该染色同构的个数。如果颜色出现的最小周期为\(d\),易知共可以得到\(d\)个不同的染色,则有\(n^m=\sum\limits_{d|m}dM(d)\),其中\(M(d)\)是最小周期为\(d\)染色数(同构意义下)。利用反演公式可以得到\(mM(m)=\sum\limits_{d|m}\mu(\dfrac{m}{d})n^d\),从而有环状字的计数公式(12)。
\[C_n(m)=\sum_{d|m}\sum_{d'|d}\mu(\dfrac{d}{d'})\dfrac{n^{d'}}{d}\tag{12}\]
2.2 Pólya计数定理
现在对问题做一般性的讨论,先假设原像是可区分的,在其上进行染色,得到了染色方案集\(X\)。还有对原像拓扑(不含颜色)进行同构置换的变换集\(G\),对任意\(g\in G\),它都是一个变换\(g:X\to X\)。当对\(x_1,x_2\in X\),当存在\(g\in G\)使得\(g(x_1)=x_2\)时,称\(x_1,x_2\)是等价的,而我们的问题就是求等价类的个数。
容易证明对每个拓扑结构,其所有的同构置换在复合运算下是封闭的,从而构成一个群。又由于它是置换群的子集,故也称对称群。\(G\)对\(X\)的变换满足条件(13),该变换是\(G\)在\(X\)上的“作用”,你需要先回顾一下“群的作用”相关知识。从两个维度分别讨论\(g(x)=x\),可以得到等价类的个数\(N(G)\)满足式(14)的Burnside定理,其中\(F_g\)表示满足\(g(x)=x\)的\(x\)的个数。如果对每个\(x\in X\)加权\(w(x)\),并使得同一等价类中的元素权值相同,则有Burnside定理的加权版(式(15)),其中\(x_k\)是第\(k\)的等价类的代表元。
\[(g_1g_2)(x)=g_1(g_2(x));\;\;e(x)=x\tag{13}\]
\[N(G)=\dfrac{1}{|G|}\sum_{g\in G}|F_g|\tag{14}\]
\[\sum_{k=1}^{N(G)}w(x_k)=\dfrac{1}{|G|}\sum_{g\in G}(\sum_{x\in F_g}w(x))\tag{15}\]
在染色问题中,我们比较关心一个染色方案使用的颜色组合,为了体现这个信息,给每个颜色赋上权值\(y_i\)。而一个染色方案的权值则是\(y_1^{k_1}y_2^{k_2}\cdots y_n^{k_n}\),其中\(k_i\)是颜色\(i\)出现的次数,且有\(k_1+k_2+\cdots+k_n=m\)。式(15)包含了所有染色方案(同构意义下)的权值,其中我们可以得到每种颜色组合\(k_1,k_2,\cdots,k_n\)下染色方案的个数。当然式(15)的计算是通过右边的式子得到的,右边聚焦于每一个置换\(g\)本身的性质,使得问题只与拓扑结构有关。
我们知道每个置换\(g\)其实是一些轮换的组合,比较显然(也很关键),\(g(x)=x\)的充要条件是同一轮换中的颜色相同。这里借用母函数的思想来计算\(F_g\)的权重,对长度为\(k\)的轮换,所有可能的权重之和是\(y_1^k+y_2^k+\cdots+y_n^k\)。从而对\(1^{\lambda_1}2^{\lambda_2}\cdots m^{\lambda_m}\)型置换\(g\)的,\(F_g\)的权重如式(16)。为了表述方便,把式(17)称为\(G\)的轮换指标(cycle index),显然当\(\delta_k=y_1^k+y_2^k+\cdots+y_n^k\)时便得到权重的完整表达式,它也被称为式样清单。特别地,取\(y_1=y_2=\cdots=y_n=1\)(即\(\delta_1=\delta_2=\cdots=\delta_m=n\)),便得到所有式样的个数(染色数)\(P_G(n,\cdots,n)\),这些结论就是波利亚(Pálya)计数定理。
\[w(F_g)=\prod_{k=1}^n(y_1^k+y_2^k+\cdots+y_n^k)^{\lambda_k}\tag{16}\]
\[P_G(\sigma_1,\cdots,\sigma_m)=\dfrac{1}{|G|}\sum_{g\in G}\sigma_1^{\lambda_1(g)}\cdots\sigma_m^{\lambda_m(g)}\tag{17}\]
2.3 典型例子
波利亚定理采用了类似母函数的思想,能够准确地完成自动计数,但结论并没有给出最终计数值,所以它更多的在于其理论价值。下面以图中三种拓扑结构为例,阐述波利亚定理的应用,而问题的关键其实就是式(17)的计算。
首先是有向环,显然它的对称子群是一个\(m\)阶循环群\(C_m=\{g,g^2,\cdots,g^m=e\}\),其中\(g\)是单步旋转。容易知道,\(g^k\)是\((k,m)\)个\(\dfrac{m}{(k,m)}\)阶轮换之积,其中\((k,m)\)是最大公约数的记号。反过来考虑,对任意\(d|m\),有\(\varphi(\dfrac{m}{d})\)个\(g^k\)的轮换指标是\(\sigma_{m/d}^d\)。所以其轮换指标是式(18),进而得到环状字的个数式(19),它和式(12)其实是等价的(\(\varphi(m)=\sum\limits_{d|m}\mu(d)\frac{m}{d}\))。
\[P_{C_m}=\dfrac{1}{m}\sum_{d|m}\varphi(\dfrac{m}{d})\sigma_{m/d}^d=\dfrac{1}{m}\sum_{d|m}\varphi(d)\sigma_d^{m/d}\tag{18}\]
\[C_n(m)=\dfrac{1}{m}\sum_{d|m}\varphi(d)n^{\frac{m}{d}}\tag{19}\]
再来看无向环,一个典型问题就是用不同颜色的珍珠能串成多少个不同的项链。它和有向环不同的是还可以进行翻转,它的对称子群\(D_m=\{g,g^2,\cdots,g^m=e,ag,ag^2,\cdots,ag^m=a\}\)被称为二面体群。其中后\(m\)个是翻转变换,当\(m\)是奇数时是\(\dfrac{n-1}{2}\)个对换,当\(n\)为偶数时,一半是\(\dfrac{n}{2}\)个对换,一半是\(\dfrac{n-2}{2}\)个对换,翻转的轮换指标如式(20)。
\[\sum_{k=1}^mw(ag^k)=\left\{\begin{matrix}\dfrac{1}{2}x_1x_2^{\frac{m-1}{2}},\;\;\;\;\;\;\;\;\;\;\;&\text{if m is odd}\\\\\dfrac{1}{4}(x_2^{\frac{m}{2}}+x_1^2x_2^{\frac{m-2}{2}}),&\text{if m is even}\end{matrix}\right.\tag{20}\]
最后来看立方体,立方体的对称群被称为立方体的旋转群,除了单位元外,还有以下三类旋转:(1)3*3=9个以对面中心为轴的旋转;(2)2*4=8个以过对顶点直线为轴的旋转;(4)1*6个以过对边中点直线为轴的旋转。这些变换可以分别作用在顶点、边和面上,其对应的轮换指标分别为如下三式所示。
\[P_0=\frac{1}{24}(x_1^8+9x_2^4+6x_4^2+8x_1^2x_3^2)\;\;\;\;\;\;\tag{21}\]
\[P_1=\frac{1}{24}(x_1^{12}+3x_2^6+6x_4^2+8x_3^4+6x_1^2x_2^5)\;\tag{22}\]
\[P_2=\frac{1}{24}(x_1^6+3x_1^2x_2^2+6x_1^4x_4+6x_2^3+8x_3^2)\tag{23}\]
• 讨论\(n\)种颜色串成的项链种数,包括规定颜色数量的情况;
• 讨论\(n\)种颜色涂色立方体点、边、面的种数,包括规定颜色数量的情况。