基本概念
并查集是一种维护集合的数据结构,“并”,“查”,“集” 三个字分别取自 Union(合并),Find(查找),Set(集合)。并查集是若干个不相交集合,能够在 \(O(1)\) 实现两个集合的合并,判断两个元素是否属于同一集合应用,如其求无向图的连通分量个数、实现kruskal算法求最小生成树。
并查集的实现方法就是一个数组:
int pre[N];其中 pre[i] 表示元素 i 结点的父节点,pre[i] 和 i 结点属于同一集合。例如:pre[1] = 2 就表明元素1的父节点是元素2,元素1和元素2属于同一集合。如果 pre[i]==i 则说明元素 i 是该集合的根结点,对于同一个集合来说,只存在一个根结点。
实现
准备工作
初始化一个pre数组。用于记录了每个节点属于哪个集合;初始时数组内的值与数组的下角标一致。即每个数字都自己一个集合。
void initialize(int n) {
for (int i = 1; i <= n; i++) {
pre[i] = i;
}
}查找操作
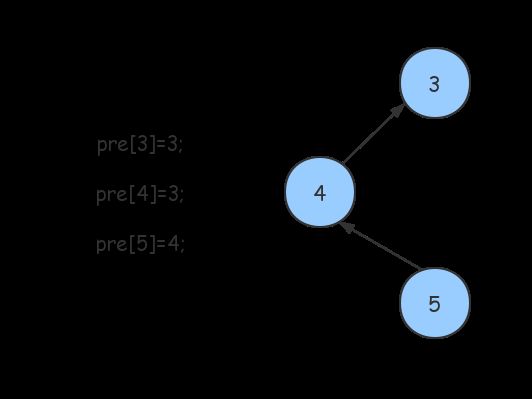
查找的目的是找到集合的 根结点 Big Boss,而不是前驱,因为前驱不一定是根结点,比如图中的5,我们要找到的是3,而不是4。
看这幅图,我们可以知道,当出现 pre[x]==x 时,证明找到了 Big Boss。
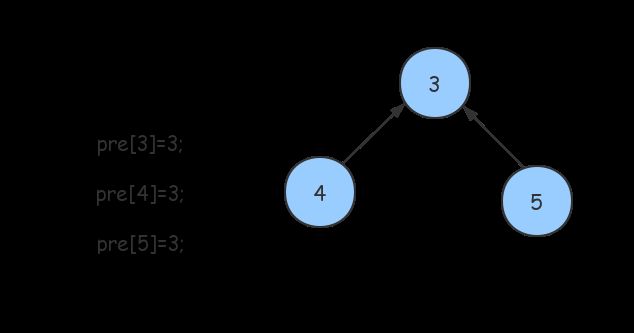
这里出现了一个问题,5和4的“顶头上司”都是3,但是5却要多走了一步,如果这个层级更多,那势必会降低算法的效率。
于是就有了在查找过程中的路径压缩
//查找
int Find(int x) {
if (pre[x] == x)return x;
return pre[x] = Find(pre[x]);
////你爸爸的爸爸就是你的爸爸
}合并操作
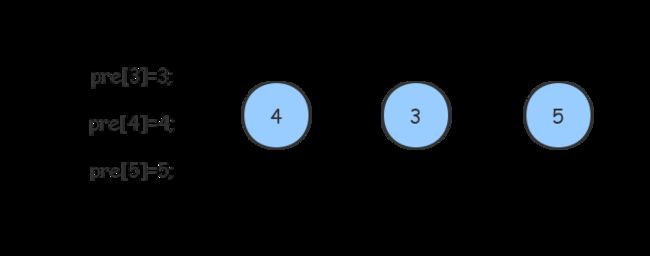
初始三个节点,各自为一个集合
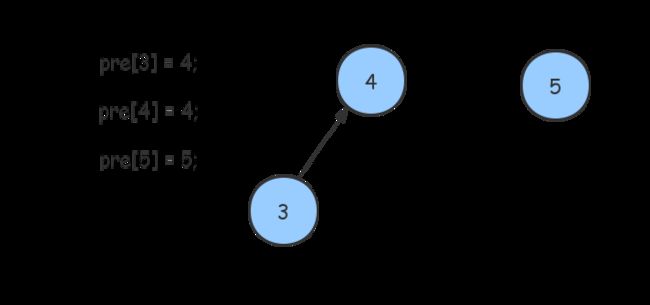
如下图,合并3,4操作,此时3和4合并为一个集合。3挂在4上,还是4挂在3上都是一样的,它们都表示3和4是同一个集合,只是集合的Big Boss不一样。
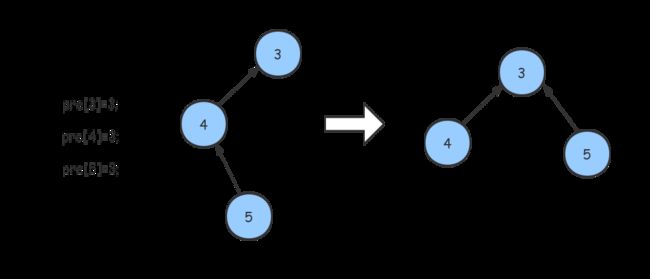
我们继续进行合并4,5操作,通过路径压缩我们获得了右边的形式,此时三个数已经为同一个集合了。
//合并
void Union(int x, int y) {
int fx = Find(x), fy = Find(y);
//如果x,y已经是同一集合了,返回
if (fx == fy) return;
//这里通过深度来确定fx挂fy上,还是fy挂在fx上,实际意义不大,就简单点写了。
pre[fy] = fx;
}完整代码,这鬼东西好用就好用在很短,真的太好写了
int pre[5001];
void initialize(int n) {
for (int i = 1; i <= n; i++) {
pre[i] = i;
}
}
int Find(int x) {
if (x == pre[x])return pre[x];
else return pre[x] = Find(pre[x]);
}
void Union(int x, int y) {
int fx = Find(x), fy = Find(y);
if (fx == fy) return;
pre[fy] = fx;
}例题
标准模板题
HDU 1232 :http://acm.hdu.edu.cn/showproblem.php?pid=1232
基本思想是:N个节点,最少需要 N-1 根线连起来。 把输入的城镇全部进行Union,如果这两个城镇不连通,N--,最后输出 N - 1就是答案。
#include
int Pre[1001];
//查找
int Find(int x) {
if (Pre[x] == x)return x;
return Pre[x] = Find(Pre[x]);
}
//合并
void Union(int x, int y, int &n) {
int fx = Find(x), fy = Find(y);
if (fx == fy) return;
Pre[fx] = fy;
n--;
}
int main() {
int n, m;
while (~scanf("%d", &n)) {
if (n == 0) break;
for (int i = 0; i <= n; i++) Pre[i] = i;
scanf("%d", &m);
while (m--) {
int c1, c2;
scanf("%d%d", &c1, &c2);
Union(c1, c2, n);
}
printf("%d\n", n - 1);
}
return 0;
} 最小生成树
题目链接:https://www.luogu.org/problem/P3366
题解: https://www.cnblogs.com/czc1999/p/11735791.html
求连通分量个数
并查集
求连通块数量,没找着简单的模板题,代码比较容易理解。
#include
using namespace std;
int pre[maxn];
int Find(int x) {
if (pre[x] == x)return x;
return pre[x] = Find(pre[x]);
}
void Union(int x, int y) {
int fx = Find(x), fy = Find(y);
if (fx == fy) return;
pre[fx] = fy;
}
int main(){
int m, n;
cin >> n;
for (int i = 0; i < n; i++) pre[i] = i;
cin >> m;
while (m--) {
int c1, c2;
cin >> c1 >> c2;
Union(c1, c2);//两点之间有路的属于同一个连通块,合并起来
}
int cnt = 0;
for (int i = 0; i < n; i++) {
if (pre[i] == i) cnt++; //有多少个根结点,就有多少个连通块
}
cout << cnt << endl;
return 0;
}
DFS
写了玩的
#include
using namespace std;
int m, n;
int cnt = 0;
int maze[500][500];
bool book[500][500];
int dir[4][2] = { {0,-1},{0,1},{-1,0},{1,0} };
void dfs(int x, int y) {
for (int i = 0; i < 4; i++) {
int tox = x + dir[i][0], toy = y + dir[i][1];
if (!book[tox][toy] && maze[tox][toy] == 1 && (tox >= 0 && tox < m && toy >= 0 && toy < n)) {
book[tox][toy] = true;
dfs(tox, toy);
}
}
return;
}
int main() {
cin >> m >> n;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> maze[i][j];
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (maze[i][j] && !book[i][j]) {
dfs(i, j);
cnt++;
}
}
}
cout << cnt;
return 0;
}
BFS
#include
#include
#include
using namespace std;
struct node {
int x;
int y;
node(int x, int y) :x(x), y(y) {};
};
queue q;
int maze[105][105];
bool book[105][105];
int m, n;
int dir[4][2] = { {0,-1},{0,1},{-1,0},{1,0} };
void bfs(int x1, int y1) {
node nn;
nn.x = x1; nn.y = y1;
while (!q.empty()) q.pop();
q.push(nn);
book[x1][y1] = true;
while (q.empty() == false) {
node now = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int tox = now.x + dir[i][0];
int toy = now.y + dir[i][1];
if (!book[tox][toy] && maze[tox][toy] == 1 && (tox >= 0 && tox < m && toy >= 0 && toy < n)) {
book[tox][toy] = true;
q.push(node(tox, toy));
}
}
}
}
int main(int argc, char** argv) {
cin >> m >> n;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> maze[i][j];
}
}
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (maze[i][j] && !book[i][j] ) {
bfs(i, j);
ans++;
}
}
}
cout << ans << endl;
return 0;
}