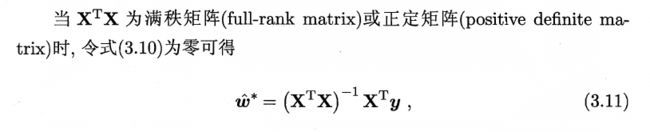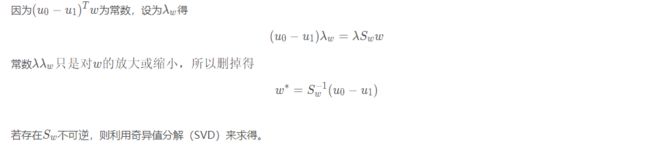1、线性回归
线性回归应该是形式最简单的机器学习方法了,但简单并不代表无用,实际上我以前学习统计课程的时候,很大篇幅都在线性模型上,一来是因为很多情形下线性模型已经足够用且可解释性良好,二来通过非线性函数映射的方法我们很容易将线性模型推广至“广义线性模型”。
由于在编程实现的时候,用矩阵和向量进行运算具有讲好的并行性,可以提升算法效率,因此一般我们把模型表示成矩阵和向量的形式:
上述解最小二乘法的过程并不复杂,需要注意的点是这里的公式解建立在满秩的基础上,若不满秩,则可能的解有多个,这时候有两种解决方法,要么把可能解都试一下,选一个最好的,要么通过某种方法使解唯一。这两种方法看似不同,其实本质上是一样的,都是要选定某种标准找到可能解中较好的那个,就好像我们给申报奖学金的同学排名,首先看绩点,如果最后两个同学绩点相同,那我们就选择综测分数高的,我们现在做的事就是在两个模型均方误差相同的情况下再设置一个评价标准,使得我们找到唯一的最优解。这里西瓜书上说常用的方法是添加正则项。加L2正则项的线性回归也称为Ridge Regression:
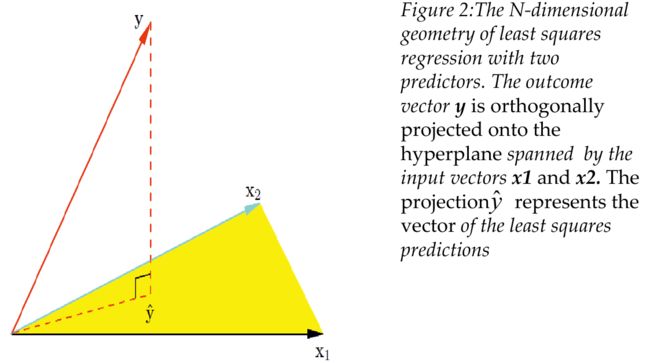
这里再回顾一下我之前在课上学过的最小二乘的几何理解:
这里的黄色平面就是我们选定的特征的张成空间,所有特征的线性组合都在这个张成空间中,为了更好的拟合y,我们只需要找到张成空间中和y差距最小的向量,当这个最小的差距定义为y到张成空间的垂直距离时,我们就找到了张成空间中和y差距最小的向量,即y在张成空间上的投影,这和我们最小二乘法的解是一致的。
2、Logistic Regression(对数几率回归)
Logistic Regressio被称为对数几率回归我是第一次见,在此之前我一直叫它逻辑回归,无所谓啦,怕混淆写英文就好。这个Logistic Regression 虽然名字叫回归,却是不折不扣的分类方法。
经典的分类方法(也是神经网络的爸爸)感知机(perceptron)是通过一个sign函数对模型进行归类的:
也就是说我们最终得到的就是分类结果0/1。有没有一种方法让我们不仅能看到分类结果,还能看到我们预测的样本属于某个种类的概率大小呢?这在现实生活中其实很常见,比如医生告知病人患病概率70%,亲子鉴定结果吻合概率为99.99%,这都是在声明样本属于某个种类的概率大小。直接的想法就是把sign函数里的线性表达式的值拿出来,“负的越多”代表这个点为0类的可能性越大,同理“正的越多”代表这个点为1类的可能性越大。接下来我们只需要把这些数值归到0~1区间就可以代表概率了。
Logistic Regression就是这样一种“软分类”方法,它通过一个logistic function把我们的线性表达式的值映射到了0~1区间上:
接下来是模型的求解,西瓜书上写的比较清楚,这里加上对公式3.27的推导(https://datawhalechina.github.io/pumpkin-book/#/chapter3/chapter3)
其实这部分推导细节并不是我关注的重点,我注意到的是这里用的极大似然法(MLE)的使用,MLE是频率学派的经典方法,一般和贝叶斯学派的贝叶斯估计放在一起比较,两者的差异在于,MLE假定模型服从某种分布,分布的参数是一个未知的固定值,我们通过极大化likelihood来确定一组参数,使得产生当前样本的可能性最大。而贝叶斯估计则把参数看作是随机变量,然后通过计算后验概率找到参数最有可能的值。而这里作者似乎融合了两种方法,用后验概率去做了MLE,这是比较有意思的地方。
3、线性判别分析(LDA)
LDA是一个非常经典的统计学方法,由Fisher在1936年提出。LDA的思想非常简单,西瓜书上总结的很好:给定训练集,设法将样本点投影到一条直线上,使得同类样本投影点尽可能接近,不同类样本投影点尽可能远离:
这里需要注意的是协方差的理解。曾经我还年少轻狂地在班里的公众号上发过一篇长文,讲解方差和协方差,现在翻出来看,真是羞耻满满……当然其中有些内容对于复习协方差的概念还是有帮助的。下图引自whuber的回答:
首先,我们把观测值写成点坐标(x,y)的形式,并在坐标系中描出。
然后,我们考虑这些点所有的两两组合,对每个点对,如果一个点在其中一个点左下方(也就是两坐标值都小于另一点),那么我们画出包含这两个点的最小矩形(也就是以这两个点为顶点的矩形)并涂成红色,如果一个点在另一个点的右下方,重复以上操作,并把矩形涂成蓝色。
涂色的意义是什么呢?我们令红色表示“正”,蓝色表示“负”,如果某个区域被涂了多次颜色,那么会改变颜色的深浅,规定如下:
(1) 如果一个区域被涂了相等次数的红色和蓝色则区域为白色(即未涂色状态)
(2) 如果一个红色区域再涂一次红色会加深此区域的“红色等级”(即颜色更深)
(3) 蓝色的规则与2相同
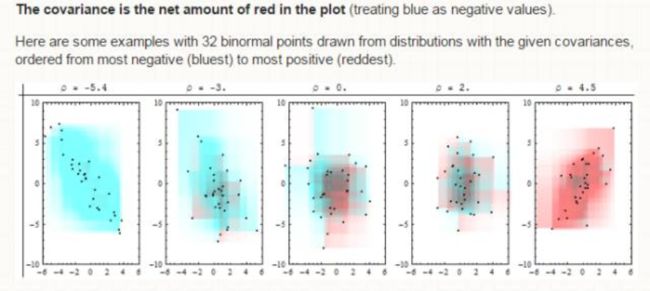
协方差就是涂色后红色区域减掉蓝色区域的大小。下面是32个点的示例:
这个解释牛逼的地方除了直观,还在于它能解释几乎所有协方差的性质:
(1) 协方差的大小和x,y轴的标度成正比(实际上是说协方差受量纲影响)。
(2) 协方差衡量的是线性相关性。这点怎么理解呢?直线是最忠贞的,她们沿着一个方向走到世界尽头,绝不变心。而曲线会拈花惹草,四处逗留。也就是说,在非线性的情形下,我们不能简单的通过两个点的方位来确定矩形的颜色(或者说“正负”)了,比如一条开口向下的抛物线,它前半段两坐标同向变化算是“正”,后半段两坐标同向变化就算是“负”了,所以我们的协方差只针对线性相关性。
(3) 对异常值的敏感性。这个很好说了,如果有一个点偏离很大,就会形成若干个巨大的矩形,直接影响结果。
至此,我们就对协方差的概念有了直观的理解,回到之前的公式:
从上面对协方差的解释我们看到,协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。这点要注意。
另外我们知道,协方差矩阵是半正定的,因此是非负的,这是理所当然的,因为样本点的投影都在一条直线上,它们的协方差必然是非负的。
接下来我们看如何求解:
(自https://blog.csdn.net/qq_34553043/article/details/82153896)
上述过程值得注意的地方有两个,一个是拉格朗日乘子法的运用,另一个是注意为标量,并不会对最终解得的w的方向有影响,因此为了简化可以删去。
书上还提到,考虑到数值解的稳定性,在实践中通常先对进行奇异值分解,即,然后由求逆。
对SVD理解一般,这里特地学习一下,记录于https://www.jianshu.com/p/8c7dac32620f
接下来是LDA在多分类任务当中的应用了,总体思路和二分类相同,重要的是理解为什么LDA可以有效降维。以下截自https://blog.csdn.net/hohaizx/article/details/78165786
这里有两个地方需要注意:
一是矩阵的构成,我们看到,各列是我们希望投至的超平面的各维的基向量,以之前的二维情形举例,实际上只包含一列,就是我们要投至的直线的基向量。西瓜书上取的的列数是类别数减1,然后最后解得的的秩将不超过类别数减1,从而远小于数据的原有属性数(因为通常情况下数据的属性数要远大于类别数)
二是对于西瓜书上为什么要用矩阵的迹的解释——矩阵的迹等于矩阵特征值之和,而我们在特征值分解中学过,矩阵特征值是沿对应的特征向量的数据的方差,所以这里的迹衡量了投影后的点在各坐标轴(即特征向量)方向上的方差大小。
4、多分类学习
很多情况下,我们基于一些基本策略,利用二分类学习器来解决多分类问题。多分类学习的基本思路是将任务分解成多个二分类问题进行求解。最经典的拆分策略有三种:
“一对一”(OvO)“一对其余”(OvR)“多对多”(MvM)
(1)OvO
OvO将N个类别两两配对,产生个分类任务。在测试阶段,新样本将同时提交给所有分类器,于是我们得到个分类结果,最终结果通过投票法产生——把预测的最多的类别作为最终分类结果。
(2)OvR
OvR每次将一类样本作为正例,其它所有类的样本作为反例,训练N个分类器。在测试阶段,若仅有一个分类器预测为正例,则对应类别为最终分类结果,若有多个分类器预测为正类,则通常考虑各分类器的预测置信度,选择置信度最大的类别标记作为最终分类结果。
上图直观地表示了OvO和OvR的运行过程。
关于OvO和OvR的比较,值得注意的地方是两者的训练开销。直觉上讲,OvO的训练开销比OvR大,因为它需要训练的分类器数目较多,但OvO每个分类器仅用到两个类别的样例,而OvR每个分类器均使用全部样例。因此在类别很多时两者开销差不多。这里我们可以通过简单的例子说明这一点,假如各个类别数据一样多,则OvO和OvR训练用到的总数据之比为:
(3)MvM
MvM是每次将若干类作为正类,若干其他类作为负类。OvO和OvR都是MvM的特例。MvM的正负类构造有特殊设计,常用的技术为纠错输出码(EOOC)。
EOOC的工作过程分为编码和解码两步:
上图就是EOOC的工作原理。解码阶段,各分类器的预测结果联合起来形成了测试示例的编码,该编码与各类对应的编码比较,距离最小的编码对应的类别为预测结果。
EOOC的优点在于其对分类器有一定的容错和修正能力。对同等长度的编码,理论上说,任意两个类别编码的距离越远,纠错能力越强。
5、类别不平衡问题
其实所谓的类别不平衡问题,指的是不同类别样本数目相差很大。实际上,按上图的说法,只要训练集中正负例数目不同,就称为类别不平衡了。因为通常我们做预测的时候,只要预测样本属于正类或负类的概率大于50%,就将样本预测为此类了。这基于的假设就是正负类样本相同。
当我们没有分类器的时候,我们可以统计出训练集中正负样本所占的比例。比如正例60%,负例40%,那么此时我任意抽取一个样本点,都可以说这个样本点属于正例的概率为60%,属于负例的概率为40%。因此分类器做出的预测至少要比没有分类器的时候更有把握,所谓更有把握,就是当我意抽取一个样本点,我的分类器可以判断出这个样本点属于正例的概率大于60%,比如80%,这就说明我的分类器确实学到了一些关于数据的特征,能做出更有把握的预测了。
这里所谓的再缩放(再平衡)策略其实就是把(3.47)右边的式子移到左边了,从而得到的新的指标和1比较即可。
这里西瓜书上提出,再缩放的思想很简单,但以上操作基于一个假设:我们能够基于训练集观测到的几率推测真实几率,这要求我们的训练集是总体的无偏采样,这一点通常很难做到。不过当我们的训练集足够大的时候,我们可以由Hoeffding's Inequality得到观测几率和真实几率在很大的概率下相差不大。
但当训练集不够大的时候,我们就需要采取一定的措施。假设现在训练集中正例较少,负例较多。
(1)欠采样。即去除一些负例使得正负例数目相当。这是最简单粗暴的方法了,优点是训练开销小,缺点则是损失了一部分本可以用来训练的数据。不过集成学习机制可以解决这个问题,例如将反例划分为几个不同的集合供不同的学习器使用,然后把各学习器集成起来,这样在全局看来不会损失重要信息。
(2)过采样。即增加一些正例使得正负例数目相当。这里需要注意的是,增加的正例不能从已有的正例中直接选取,否则会出现过拟合,通常采用对已有正例插值的方式产生额外正例。
(3)直接基于原始训练集学习,并用再缩放对决策进行修正。