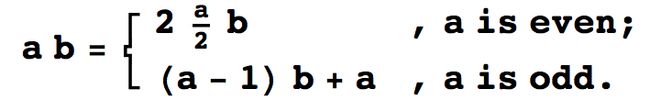TMD谁把 list 翻译成“列表”的,明明是“序列”的意思嘛
——Pope, 2012
本科的时候啃过SICP,好像只读完了前两章。现在忙了,反而觉得应该好好看看,连以前不入眼的练习也决定一道道过。
解释器是用的DrRacket,前身是DrScheme。不知道为啥改了这么个怪名字-_-!
练习1.2
; Exercise 1.2
(/ (+ 5
4
(- 2
(- 3
(+ 6
(/ 4 5)))))
(* 3
(- 6 2)
(- 2 7)))
让我惊奇的是DrScheme居然返回-37/150!后来才知道Scheme里有种类型叫rational numbers。
练习1.3
; Exercise 1.3
(define (single? lst)
(null? (cdr lst)))
(define (minimum lst)
(if (single? lst)
(car lst)
(min (car lst)
(minimum (cdr lst)))))
(define (sum-of-larger a b c)
(- (+ a b c)
(minimum (list a b c))))
(sum-of-larger 2 4 5)
Scheme用起来不爽的原因:
一是很多“脚手架”都得自己搭,比如,判断是否为单一元素(single?)、序列的尾(有“头(first)”,但是木有尾(tail));
二是提供的“脚手架”不好用,比如,求序列的最大/最小值,参数居然不能是序列,非得把要比较的元素一个个传进去,像这样(min 1 2 3)(当然,你也可以(apply min '(1 2 3)),但毕竟要转一道弯)。
看看人家Ruby, [1, 2, 3].first, [1, 2, 3].last, [1, 2, 3].min,多会来事
练习1.5
; Exercise 1.5
(define (p) (p))
(define (test x y)
(if (= x 0)
0
y))
;(test 0 (p))
练习1.5 很有意思(和后面的1.6一样)考察你对正则序(normal order)和应用序(applicative order)的理解。按照正则序求值是“完全展开而后规约”,而目前解释器实际采用的是“先对参数求值,而后将其代人到表达式中的所有同一参数”的应用序求值。应用序的好处就是可以避免重复对同一参数求值。
不管过程如何,先代到DrScheme里跑一遍。结果死循环,栈溢出了。稍作分析即可知道,DrScheme采用的是应用序,会先对参数求值。这样,0还是0,但对函数调用(p)求值却会进入死循环,直到栈溢出。如果解释器采用了正则序就会立即返回0,因为采用了正则序的解释器会先把(test 0 (p))展开为
(if (= 0 0)
0
(p))
而if是预置函数,采用的是短路求值,即一旦判断为真就不会考虑else-子表达式。这样,采用了正则序的解释器安全返回0,结束求值过程。
但这并不是说正则序比应用序好,你总能针对某种策略做出假死的情况来。
; 1.1.7
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x)
x)))
(define (improve guess x)
(average guess (/ x guess)))
(define (average x y)
(/ (+ x y) 2))
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (square x) (* x x))
(define (sqrt x)
(sqrt-iter 1.0 x))
(sqrt 9)
练习1.6
; Exercise 1.6
(define (new-if predicate then-clause else-clause)
(cond (predicate then-clause)
(else else-clause)))
(define (sqrt-iter2 guess x)
(new-if (good-enough? guess x)
guess
(sqrt-iter2 (improve guess x)
x)))
(define (sqrt2 x)
(sqrt-iter2 1.0 x))
;(sqrt2 9)
和练习1.5相似。不同的是,这里想强调一点,“管你是数据还是函数,众生平等,但有些函数比其他函数更平等”。这部分函数就是预置函数。虽然new-if功能上与if完全一样,但new-if毕竟是个普通函数,所有传入的参数都会先行求值(应用序嘛);if就不一样了,人家是大妈生的,只在判决出来了,才选择性地对子表达式求值,所以不会陷入无穷递归(在本题中)。
练习1.7
; Exercise 1.7
(define (sqrt-iter3 guess old-guess x)
(if (good-enough2? guess old-guess x)
guess
(sqrt-iter3 (improve guess x)
guess
x)))
(define (good-enough2? guess old-guess x)
(< (abs (- 1 (/ guess old-guess))) 0.01))
(define (sqrt3 x)
(sqrt-iter3 1.0 x x))
(sqrt3 2)
练习1.8
; Exercise 1.8
(define (cbrt-iter guess old-guess x)
(if (good-enough2? guess old-guess x)
guess
(cbrt-iter (cb-improve guess x)
guess
x)))
(define (cb-improve guess x)
(/ (+ (/ x (square guess))
(* 2 guess))
3))
(define (cbrt x)
(cbrt-iter 1.0 x x))
(cbrt 8)
练习1.9
; Exercise 1.9
; (define (+ a b)
; (if (= a 0)
; b
; (inc (+ (dec a) b))))
; (+ 4 5)
; (inc (+ 3 5))
; (inc (inc (+ 2 5)))
; (inc (inc (inc (+ 1 5))))
; (inc (inc (inc (inc (+ 0 5)))))
; (inc (inc (inc (inc 5))))
; (inc (inc (inc 6)))
; (inc (inc 7))
; (inc 8)
; 9
; (define (+ a b)
; (if (= a 0)
; b
; (+ (dec a) (inc b))))
; (+ 4 5)
; (+ 3 6)
; (+ 2 7)
; (+ 1 8)
; (+ 0 9)
; 9
练习1.10
; Exercise 1.10
(define (A x y)
(cond ((= y 0) 0)
((= x 0) (* 2 y))
((= y 1) 2)
(else (A (- x 1)
(A x (- y 1))))))
(A 1 10)
(A 2 4)
(A 3 3)
练习1.11
; Exercise 1.11
; (define (f n)
; (if (< n 3)
; n
; (+ (f (- n 1))
; (* 2 (f (- n 2)))
; (* 3 (f (- n 3))))))
(define (f n)
(define (iter a b c n)
(if (= n 2)
a
(iter (+ a (* 2 b) (* 3 c)) a b (- n 1))))
(iter 2 1 0 n))
(f 5)
练习1.12
; Exercise 1.12
(define (tail lst)
(cond ((null? lst) '())
((single? lst) (car lst))
(else (tail (cdr lst)))))
(define (Pascal-triangle n)
(define (gen lst)
(define (last-line lst)
(cond ((single? lst) '())
(else (cons (+ (first lst)
(second lst))
(last-line (cdr lst))))))
(append lst
(list (cons 1
(append (last-line (tail lst))
'(1))))))
(cond ((= n 1) '(1))
((= n 2) '((1) (1 1)))
(else (gen (Pascal-triangle (- n 1))))))
(Pascal-triangle 6)
这题我自己都不知道是怎么过的,感觉Scheme的序列很诡异,序列(list)和有序对(pair)到底谁是妈啊?!R6RS(Scheme标准)里倒是给出了序列的递归定义:序列要么是个空序列;要么是个有序对,其后一部分须为序列(A list can be defined recursively as either the empty list or a pair whose cdr is a list.)。照这个定义,严格地说,任何序列的最后一个元素都必须是空序列(空序列不是有序对),因为结尾的必须是序列嘛,没说可以是元素哦。但事实上,也不会抠这死理,这种不以空序列结尾的有序对链叫做improper list(它不是list
)。注意,(a b c . d) 和(a . (b . (c . d)))是等价的。
只有弄清了序列和有序对的区别,你才能搞清楚为什么(cdr '(1 2)) 返回(2),而(cdr '(1 . 2))返回2,以及为什么(cons 8 9) 产生的是一个有序对(8 . 9),而(cons 8 '(9))生成的却是序列(8 9)。
练习1.13
要求证Fib(n)是最接近Φ^n/√5的整数,即 | Fib(n)-Φ^n/√5 | < 1。而Fib(n) = (Φ^n-γ^n) /√5, Φ = (1 + √5)/2, γ = (1 - √5)/2, 所以Φ^n/√5 - Fib(n) = γ^n/√5 = (-1)^n ((√5-1)/2)^n/√5。众所周知,(√5-1)/2是黄金分割点0.618,其除以 √5肯定比1小,所以Φ^n/√5 - Fib(n)的绝对值小于1,故得证。
现在的问题是,你怎么知道Fib(n) = (Φn-γn) /√5?
这是一个来自中学奥赛的古老技巧,不知道它是怎么来的,但它很优美地就把问题解决了,就好像从没存在过这个问题一样。
令f_n = Fib(n),设f_n - αf_(n-1) = β(f_(n-1) - αf_(n-2) ),则α + β = 1且- αβ = 1,即α = (1 + √5)/2, β = (1 - √5)/2(或者对调)
所以f_n = α^(n-1) + α^(n-2)β + ... + αβ^(n-2) + β^(n-1)(此处省去若干字)。
然后呢,我想了很久,曾试图拆成两半,利用 αβ = -1的特性来化为等比数列⋯⋯最后放弃了,因为结果很复杂。它不应长这个样子。
然后,我又看了看提示,突然意识到,曾几何时有这么个恒等式:
α^n - β^n = (α - β)(α^(n-1) + α^(n-2)β + ... + αβ^(n-2) + β^(n-1))
-_-!!
练习1.14
所需空间为调用树的高度,即n / min{coins[k]};
其所需空间的阶为Θ(n)。
设C(n, k)为以k种硬币兑换n元的方案数,coins为一数组,其元素的值为各种硬币面值,则
C(n, k) = C(n, k-1) + C(n-coins[k], k)
然后,⋯⋯,好吧,我承认,我不知道该怎么解,甚至连大致的阶也猜不出来-_-!!
练习1.15
; Exercise 1.15
(define (cube x) (* x x x))
(define (p x) (- (* 3 x) (* 4 (cube x))))
(define (sine angle)
(if (not (> (abs angle) 0.1))
angle
(p (sine (/ angle 3.0)))))
(sine 12.15)
(p (sine 4.05))
(p (p (sine 1.35)))
(p (p (p (sine 0.45))))
(p (p (p (p (sine 0.15)))))
(p (p (p (p (p (sine 0.05))))))
⋯⋯
可见p将被调用5次。
在求(sine a)的值时,需要至少n层栈,n满足:
a / 3^n < 0.1
即,n > log_3 10a
故需要的空间的阶为Θ(log n)。
因其计算过程分为递归展开至终止情况(即弧度不大于0.1)和回退两部分,故步数为所需空间的常数倍,即Θ(log n)。
为了得到调用sine的实际步数,添加一个参数c(作为累计量),返回结果变为一个有序对(正弦值, 调用次数):
(define (inc x) (+ x 1))
(define (cube x) (* x x x))
(define (p x) (- (* 3 x) (* 4 (cube x))))
(define (sine angle c)
(if (not (> (abs angle) 0.1))
(cons angle (inc c))
(let ((res (sine (/ angle 3.0) (inc c))))
(cons (p (car res)) (cdr res)))))
(sine 12.15 0) ; => (-0.39980345741334 . 6)
练习1.16
; Exercise 1.16
(define (fast-expt b n)
(define (expt-iter b counter product)
(cond ((= counter 0) 1)
((= counter 1) (* b product))
((even? n) (expt-iter (square b) (/ counter 2) product))
(else (expt-iter b (- counter 1) (* b product)))))
(expt-iter b n 1))
以b^7为例
b^7 = b^6 ·b
= (b2)3 ·b
= (b2)2 ·(b^2 · b)
= (b4)1 ·(b^2 · b)
= b4 ·(b^2 · b)
斜体部分就是product,用来存储幂为奇数时产生的尾数。
练习1.17
; Exercise 1.17
(define (double n)
(+ n n))
(define (halve n)
(/ n 2))
(define (fast-prod a b)
(cond ((= a 0) 0)
((even? a) (double (fast-prod (halve a) b)))
(else (+ (fast-prod (- a 1) b) b))))
(fast-prod 4 3)
; Exercise 1.18
(define (double n)
(+ n n))
(define (halve n)
(/ n 2))
(define (fast-prod a b sum)
(cond ((= a 0) sum)
((even? a) (fast-prod (halve a) (double b) sum))
(else (fast-prod (- a 1) b (+ b sum)))))
(define (prod a b)
(fast-prod a b 0))
(prod 5 4)
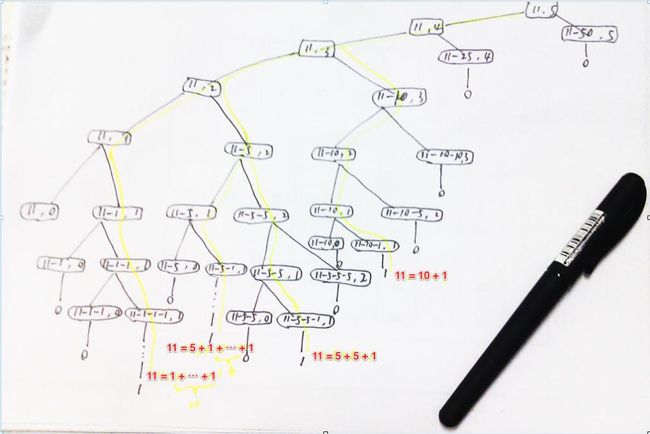
俄罗斯农民算法是这样进行的:第一乘数不断除2下取整直至为1,第二乘数不断乘2,如此罗列下来。然后把所有第一乘数为偶数的行划去,接着把第二乘数那一列加起来,即为乘积。
5 4
2 8
1 16
....20
换个写法:
5 × 4
= 4 × 4 + 4
= 2 × 8 + 4
= 1 × 16 + 4
= 0 × 16 + (16 + 4)
sum就是用来存储第一乘数为奇数时的累加值。
练习1.19
; Exercise 1.19
(define (square n)
(* n n))
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
(cond ((= count 0) b)
((even? count)
(fib-iter a
b
(+ (square p) (square q)) ; compute p'
(+ (square q) (* 2 p q)) ; compute q'
(/ count 2)))
(else (fib-iter (+ (* b q) (* a q) (* a p))
(+ (* b p) (* a q))
p
q
(- count 1)))))
(fib 7)
变换规则
a’ ← b q + a q + a p
b’ ← b p + a q
应用两次后,得:
a’ ← b Q + a Q + a P
b’ ← b P + a Q
其中,P = p^2 + q^2,Q = q^2 + 2 p q
谁想出来的,太GG神奇了!
(待续……)