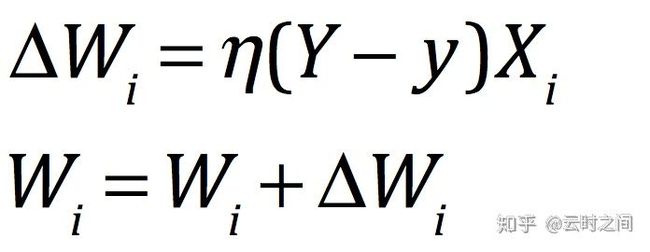今天这个文章让我们一起来学习下感知机:
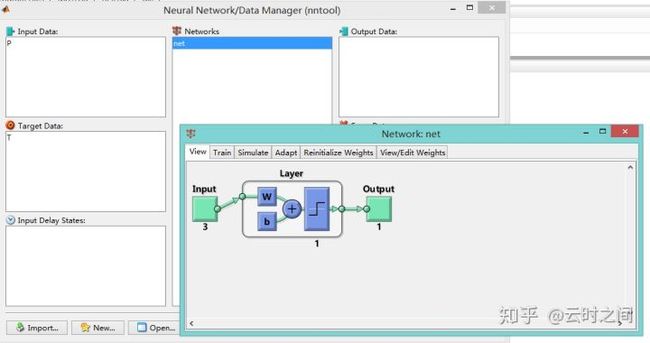
一个传统的单层感知机如上图所示,其实理解起来很简单,我们可以直接理解为输入节点接受信号之后直接传输到输出节点,然后得到结果y.
就和上图一样,我们给出了权向量W=[W1,W2,W3]=[0.3,0.3,0.3],这时候我们输入[X1,X2,X3],并且于输出节点的t相结合,这样就可以得到方程式:
y = 0.3X1+0.3X2+0.3X3+0.4
在我们给定训练数据集之后,第一次给定的权值基本不会是适合的,因此我们需要使用给定的训练数据集进行迭代学习,规则如下:
给定的测试样例为(X,Y),而如今现在的模型输出为y,此时我们要对权值进行调整:
而这里边的η被称为学习率,这个学习率∈(0,1),并且很大程度上这个学习率是根据我们的经验得到的.如果我们选择的学习率过大,容易造成权值计算的不稳定.如果选择的学习率太小,不能够充分体现出对于权值的修正,迭代次数太多.就跟我们显微镜对焦一样,左调调,右调调就会看的越来越清楚.
从上边的式子来看,如果输出的实际值y和训练集中的Y一致,则Wi就不会发生变化,从而感知机就不会发生变化,否则感知机就会根据错误的大小进行权值的处理.
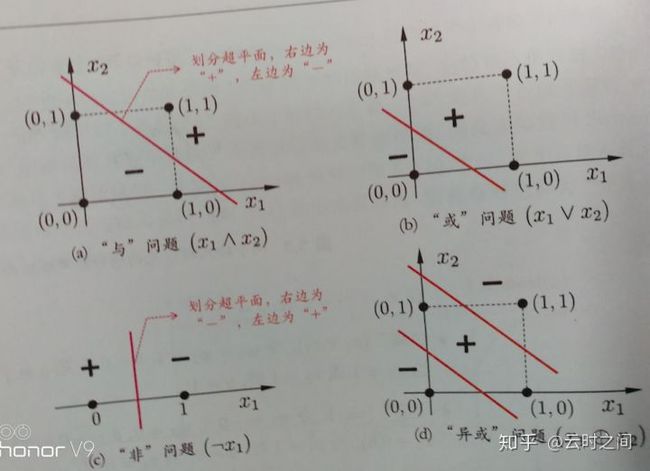
所以从上述来看,本质上感知机只能够对输出层进行处理,学习能力是很有限的,泛化能力很差.我们不妨分析下:对于与,或,非这样的问题,如图所示:
是可以形成一个线性超平面,从而进行分类划分.
如果是异或这样的问题,是无法形成一个线性超平面进行划分的.
在这里我们总结一下单层感知器的局限:
1:单层感知器没有泛化的能力
2:结构简单,激活函数只能是符号函数
3:只对于线性可分问题进行收敛,如果非线性可分问题,不会产生超平面,无法收敛.
4:如果存在离群点,则需要花费太多的训练时间.
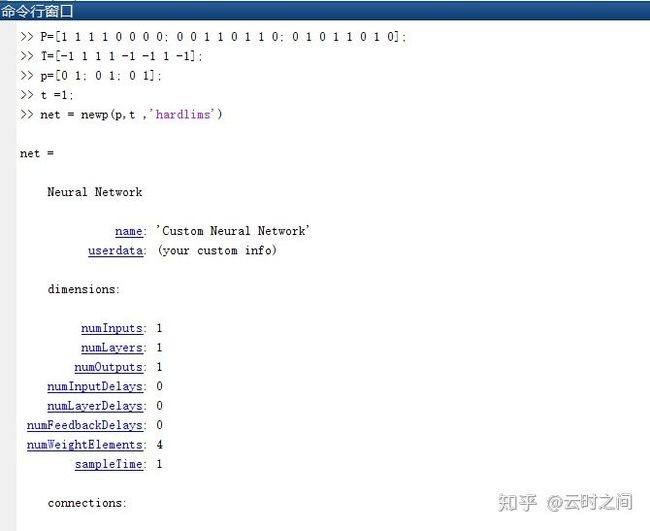
下面我们用MATLAB来实际操作搭建一个单层感知器:
首先我们在MATLAB中输入P,T,p,t,P和T是训练集和训练集结果,p,t则是模型的参数,这里我们在nevp()中使用hardlims,这个参数是单层感知机的激活函数名称.
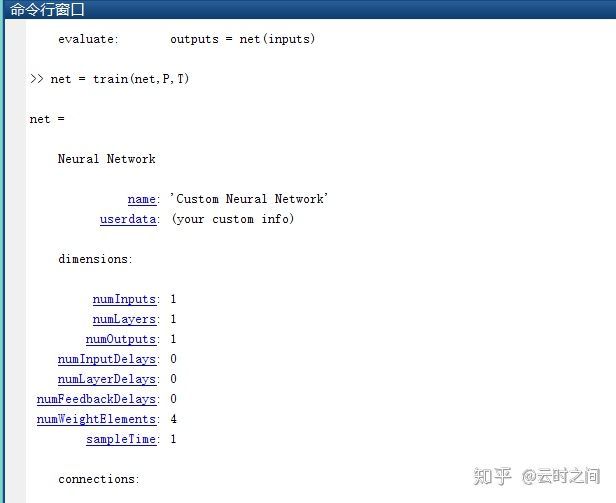
训练后我们输入测试集:
因此我们输入之后,可以得到一个正确的结果.
而MATLAB中也有一个nntool,可以使用图形化界面进行操作:
我们在命令行输入nntool.
注意选择上边的参数.
选择好输入的数据集
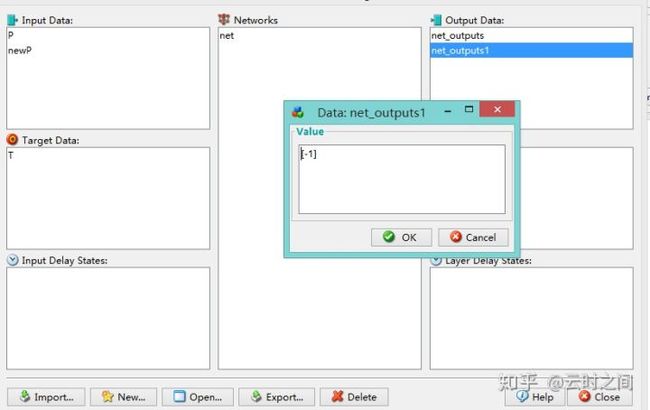
进行训练,训练后输入测试集:
输入结果,是-1,跟之前我们的测试集是一致的.
我的博客即将搬运同步至腾讯云+社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan