- 不使用指针可以键链表吗?
- 静态链表
- 用游标找到后继
- 游标与备用链表
- 初始化静态链表
- 插入与删除
- 插入操作
- 删除结点
- 静态链表小结
- 应用
- 题干:
- 题目解析:
- 代码实现
- 参考资料
不使用指针可以键链表吗?
在 C/C++ 中,我们可以利用数组实现顺序表,用指针实现链表,但是并不是所有语言都有这两种工具的,例如 python、Java 等,不过这些是面向对象的世界语言,拥有其他机制来实现指针的功能,但是对一些早期的编程语言来说,上述的链表就没有办法实现了。如果我想要在不能使用指针的情况下使用链式存储结构,应该怎么操作呢?
可以用数组代替指针实现链式存储结构,我们说链式存储结构的特点在于,存储位置可以不相邻,数据间的逻辑关系可以被描述,只要我们利用数组实现这两个需求,就可以达到用数组实现链式存储结构的目的。
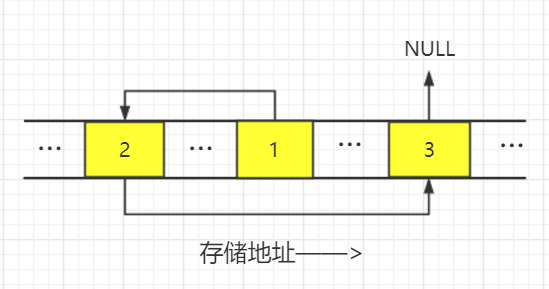
静态链表
用游标找到后继
我们定义一个结构体,这个结构体拥有两个数据域 data 和 cur,data 用来存放需要存储的数据,而 cur 则用来存储该元素对应的后继在数组中的下标,也就是说 cur 数据域相当于单链表的指针域,通过 cur 我们就能找到该元素对应的后继。cur 被称为游标,用数组实现的链式存储结构被称为静态链表。
typedef struct
{
ElemType data; //数据域
int cur; //游标
}Component,StaticList[MAXSIZE]; //为了防止溢出,数组的存储上限可以定义的大一些
游标与备用链表
静态链表能否实现类似单链表的申请、释放结点的功能,可以将这个数组分为两部分,一部分用来存储数据,另一部分作为备用链表。备用链表,即连接各个空闲位置的链表,备用链表的作用是回收数组中未被使用的存储空间,作为提供新结点的空间来源。每当我们需要新结点的时候,就把备用链表中的一个元素通过游标接入到存储数据的表上来。这个时候,就要求我们能够精准定位两个表在同一个数组中的位置,可以利用数组的第一个元素作为头结点,用于定位备用链表,用 cur 记录备用链表的第一个结点的下标,最后一个元素则充当头结点,用于定位存储数据的表,cur 存储第一个存储数据的第一个结点下标。
初始化静态链表
bool InitLinst(StaticList L)
{
int i;
for(i = 0; i < MAXSIZE - 1; i++)
{
L[i].cur = i + 1; //初始化游标
}
L[MAXSIZE - 1].cur = 0; //最后一个元素充当头结点,cur 初始化为0
}
插入与删除
当我们需要新结点的时候,就利用修改游标的关系,把备用链表的一个元素连接到主表上,删除则是把不再使用的元素用游标转移到备用链表。由此可见插入和删除操作都要特别注意对游标的精准操作操作。
插入操作
首先我们需要先模拟实现动态内存分配函数 malloc,以此实现对备用链表申请空间,函数返回备用链表中第一个结点的下标,如果备用链表没有闲置空间了,就返回0。
int SSL_Malloc(StaticList space)
{
int idx = space[0].cur; //将备用链表的第一个闲置空间的下标作为返回值,表示申请到的空间
if(space[0].cur != 0) //判断备用链表的闲置空间是否用尽
{
space[0].cur = space[idx].cur; //若没用尽,移动备用链表的第一个结点为原第一个结点的后继
}
return idx; //返回可利用的数组元素下标
}
我们自己造了动态内存分配函数,接下来就实现静态链表的插入结点,与单链表插入结点的思路一致,不同在于我们操作的不是指针域,而是游标。函数成功插入结点时返回 true,否则返回 false。
bool LinkInsert(StaticLinkList L,int idx, ElemType e)
{
int blank; //存储分配好的空闲空间下标
int prior = MAXSIZE - 1; //存储需要插入的前驱结点下标,初始化为最后一个元素
if(i < 1 || i > ListLength(L) + 1) //处理不合法插入
{
return false;
}
blank = SSL_Malloc(L); //分配空闲的元素下标
if(blank != 0)
{
L[blank].data = e; //向新节点放入数据
for(int i = 1; i <= idx - 1; i++) //获取前驱结点下标
{
prior = L[prior].cur; //通过游标遍历静态链表,直到找到 idx 的前驱
}
L[blank].cur = L[prior].cur; //修改新新结点的后继为前驱结点的后继
L[prior].cur = blank; //修改前驱结点的后继为新结点
return true;
}
return false;
}
删除结点
首先我们需要先实现结点释放函数 SSL_Free,实现的方式还是对游标的精确操作。
void SSL_Free(StaticLink L, int i)
{
space[i].cur = space[0].cur; //运用头插法的思想,修改被释放的结点的后继为备用链表的第一个结点
space[0].cur = i; //修改备用链表的第一个结点为被释放的结点
}
删除静态链表中第 i 个元素,删除的位置不合法返回 false,成功删除返回 true。
bool LinkDelete(StaticLink L, int idx)
{
int prior;
if(idx < 1 || idx > ListLength(L))
{
return false;
}
prior = MAXSIZE - 1;
for(int i = 1; i <= idx - 1; i++)
{
prior = L[prior].cur; //遍历静态链表,找到第 idx 位置的前驱
}
i = L[prior].cur; //拷贝需要转移到备用链表的元素下标
L[prior].cur = L[L[prior].cur].cur; //修改前驱结点的游标为结点后继的后继
SSL_Free(L,i); //转移元素到备用链表
return true;
}
静态链表小结
静态链表通过一个 int 类型的变量作为游标,代替了链表中指针的使用,使得数组也可以实现链式存储结构,使得数组描述的线性表在执行插入、删除操作时,不需要移动大量元素,但是静态链表并不能解决存储数据数量的上限所带来的问题,而且也失去了数组在随机读取方面的优势。静态链表是为了在没有指针及其类似语法的时候,实现链式存储结构的方式,但是目前已经很少应用这种存储结构了,不过我们对于这种别致的线性表,我们没有用到什么复杂的语法,而是灵活的应用了数组及其下标,这就强调了复杂的操作是由基本操作组合而成这种思想。
应用
题干:
题目解析:
我们来看看这道题目吧,这道题目的测试数据很别致,测试数据已经把链表单个结点的地址及其后继安排得明明白白了,那么这种数据我们用什么结构存储是最合适的?那就是静态链表,我可以开一个元素个数为100000的空间,然后按照每一组数据的结点地址,相对应位置的数组元素填充,数组元素包含两个域,分别是数据域和游标,利用游标来存储下一个结点在数组中的位置。
这样我们就把数据安排明白了,我们发现这么存数据并不是严格意义上的静态链表,因为我们在这个数组中构造备用链表。这是因为给的测试数据已经把结点的逻辑关系描述得很明白了,而且不会引入新结点,所以我们也不必多此一举,去描述备用链表。我们是虽然没有实现完整的静态链表,但是我们利用了静态链表的思想去解决这个问题。
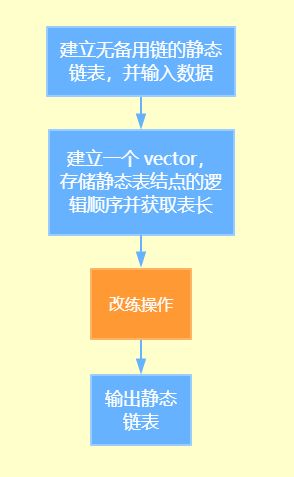
接下来就要重排链表了,不过如果直接去遍历这个链表,并修改结点,那就会出现很多问题,我们当然可以造个尾游标,从头和尾向中间移动,依次获取对应改链,但是这样无疑是很麻烦的。思考一下,如果我们已经实现知道了静态表的逻辑顺序,然后直接找到各个结点修改游标,修改的数值直接可以通过静态表的逻辑顺序来查找修改,这样就方便了很多。所以,我们可以造一个 vector 来按照表的逻辑顺序获取地址,用 vector 的目的在于,提供的数据可能有废弃结点,这种结点不会包含在表中,因此我们的思路是遍历到一个结点,就向 vector 中动态加入一个元素,由于 vector 容器是动态增长的容器,因此也不会造成空间的浪费。在获取了静态链表结点的逻辑顺序之后,我们也可以直接利用泛型算法“ .size() ”直接获取表长。
有了表长和结点的逻辑顺序,就可以通过对各个结点地址的访问,轻松达到改链的目的,我们可以对两端同时操作,一次安排两个结点,然后向中间移动。需要注意的是,如果是这么操作的话,尾结点就会丢失,也就是尾结点的后继不为 NULL,遍历时就会陷入死循环,这是我们不希望看到的。因此我们需要找到尾结点,将尾结点的后继修改为 -1。
最后,把静态表输出,大功告成!
代码实现
参考资料
《大话数据结构》—— 程杰 著,清华大学出版社
数据结构6: 静态链表及C语言实现
C语言中文网

