引言
在做KB的基础DP练习题的时候遇到了最大子序列和的变种问题,突然发现自己以前没做过解题笔记(现补上)
最大子序列和是一道经典的算法题, leetcode 也有原题《53.maximum-sum-subarray》,今天我们就来彻底攻克它。
题目描述
求取数组中最大连续子序列和,例如给定数组为 A = [1, 3, -2, 4, -5], 则最大连续子序列和为 6,即 1 + 3 +(-2)+ 4 = 6。
去
首先我们来明确一下题意。
- 题目说的子数组是连续的
- 题目只需要求和,不需要返回子数组的具体位置。
- 数组中的元素是整数,但是可能是正数,负数和 0。
- 子序列的最小长度为 1。
比如:
- 对于数组 [1, -2, 3, 5, -3, 2], 应该返回 3 + 5 = 8
- 对于数组 [0, -2, 3, 5, -1, 2], 应该返回 3 + 5 + -1 + 2 = 9
- 对于数组 [-9, -2, -3, -5, -3], 应该返回 -2
解法一 - 暴力法(超时法)
一般情况下,先从暴力解分析,然后再进行一步步的优化。
思路
我们来试下最直接的方法,就是计算所有的子序列的和,然后取出最大值。
记 Sum[i,….,j]为数组 A 中第 i 个元素到第 j 个元素的和,其中 0 <= i <= j < n,
遍历所有可能的 Sum[i,….,j] 即可。
我们去枚举以 0,1,2…n-1 开头的所有子序列即可,
对于每一个开头的子序列,我们都去枚举从当前开始到 n-1 的所有情况。
这种做法的时间复杂度为 O(N^2), 空间复杂度为 O(1)。
代码
Java:
class MaximumSubarrayPrefixSum {
public int maxSubArray(int[] nums) {
int len = nums.length;
int maxSum = Integer.MIN_VALUE;
int sum = 0;
for (int i = 0; i < len; i++) {
sum = 0;
for (int j = i; j < len; j++) {
sum += nums[j];
maxSum = Math.max(maxSum, sum);
}
}
return maxSum;
}
}
Python 3:
import sys
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
maxSum = -sys.maxsize
sum = 0
for i in range(n):
sum = 0
for j in range(i, n):
sum += nums[j]
maxSum = max(maxSum, sum)
return maxSum
空间复杂度非常理想,但是时间复杂度有点高。怎么优化呢?我们来看下下一个解法。
解法二 - 分治法
思路
我们来分析一下这个问题, 我们先把数组平均分成左右两部分。
此时有三种情况:
- 最大子序列全部在数组左部分
- 最大子序列全部在数组右部分
- 最大子序列横跨左右数组
对于前两种情况,我们相当于将原问题转化为了规模更小的同样问题。
对于第三种情况,由于已知循环的起点(即中点),我们只需要进行一次循环,分别找出
左边和右边的最大子序列即可。
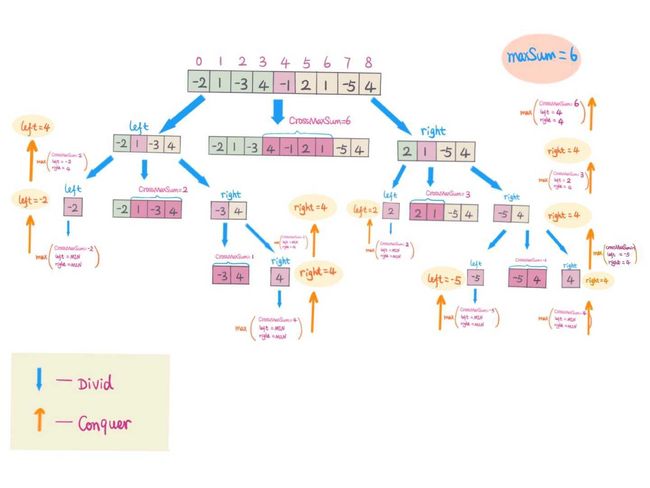
所以一个思路就是我们每次都对数组分成左右两部分,然后分别计算上面三种情况的最大子序列和,
取出最大的即可。
举例说明,如下图:
这种做法的时间复杂度为 O(N*logN), 空间复杂度为 O(1)。
代码
Java:
class MaximumSubarrayDivideConquer {
public int maxSubArrayDividConquer(int[] nums) {
if (nums == null || nums.length == 0) return 0;
return helper(nums, 0, nums.length - 1);
}
private int helper(int[] nums, int l, int r) {
if (l > r) return Integer.MIN_VALUE;
int mid = (l + r) >>> 1;
int left = helper(nums, l, mid - 1);
int right = helper(nums, mid + 1, r);
int leftMaxSum = 0;
int sum = 0;
// left surfix maxSum start from index mid - 1 to l
for (int i = mid - 1; i >= l; i--) {
sum += nums[i];
leftMaxSum = Math.max(leftMaxSum, sum);
}
int rightMaxSum = 0;
sum = 0;
// right prefix maxSum start from index mid + 1 to r
for (int i = mid + 1; i <= r; i++) {
sum += nums[i];
rightMaxSum = Math.max(sum, rightMaxSum);
}
// max(left, right, crossSum)
return Math.max(leftMaxSum + rightMaxSum + nums[mid], Math.max(left, right));
}
}
Python 3 :
import sys
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
return self.helper(nums, 0, len(nums) - 1)
def helper(self, nums, l, r):
if l > r:
return -sys.maxsize
mid = (l + r) // 2
left = self.helper(nums, l, mid - 1)
right = self.helper(nums, mid + 1, r)
left_suffix_max_sum = right_prefix_max_sum = 0
sum = 0
for i in reversed(range(l, mid)):
sum += nums[i]
left_suffix_max_sum = max(left_suffix_max_sum, sum)
sum = 0
for i in range(mid + 1, r + 1):
sum += nums[i]
right_prefix_max_sum = max(right_prefix_max_sum, sum)
cross_max_sum = left_suffix_max_sum + right_prefix_max_sum + nums[mid]
return max(cross_max_sum, left, right)
解法三 - 动态规划
思路
我们来思考一下这个问题, 看能不能将其拆解为规模更小的同样问题,并且能找出
递推关系。
我们不妨假设问题 Q(list, i) 表示 list 中以索引 i 结尾的情况下最大子序列和,
那么原问题就转化为 Q(list, i), 其中 i = 0,1,2…n-1 中的最大值。
我们继续来看下递归关系,即 Q(list, i)和 Q(list, i - 1)的关系,
即如何根据 Q(list, i - 1) 推导出 Q(list, i)。
如果已知 Q(list, i - 1), 我们可以将问题分为两种情况,即以索引为 i 的元素终止,
或者只有一个索引为 i 的元素。
- 如果以索引为 i 的元素终止, 那么就是 Q(list, i - 1) + list[i]
- 如果只有一个索引为 i 的元素,那么就是 list[i]
分析到这里,递推关系就很明朗了,即Q(list, i) = Math.max(0, Q(list, i - 1)) + list[i]
举例说明,如下图:
这种算法的时间复杂度 O(N), 空间复杂度为 O(1)
代码
Java:
class MaximumSubarrayDP {
public int maxSubArray(int[] nums) {
int currMaxSum = nums[0];
int maxSum = nums[0];
for (int i = 1; i < nums.length; i++) {
currMaxSum = Math.max(currMaxSum + nums[i], nums[i]);
maxSum = Math.max(maxSum, currMaxSum);
}
return maxSum;
}
}
Python 3:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
max_sum_ending_curr_index = max_sum = nums[0]
for i in range(1, n):
max_sum_ending_curr_index = max(max_sum_ending_curr_index + nums[i], nums[i])
max_sum = max(max_sum_ending_curr_index, max_sum)
return max_sum
解法四 - 数学分析
思路
我们来通过数学分析来看一下这个题目。
我们定义函数 S(i) ,它的功能是计算以 0(包括 0)开始加到 i(包括 i)的值。
那么 S(j) - S(i - 1) 就等于 从 i 开始(包括 i)加到 j(包括 j)的值。
我们进一步分析,实际上我们只需要遍历一次计算出所有的 S(i), 其中 i 等于 0,1,2….,n-1。
然后我们再减去之前的 S(k),其中 k 等于 0,1,i - 1,中的最小值即可。 因此我们需要
用一个变量来维护这个最小值,还需要一个变量维护最大值。
这种算法的时间复杂度 O(N), 空间复杂度为 O(1)。
其实很多题目,都有这样的思想, 比如之前的《每日一题 - 电梯问题》。
代码
Java:
class MaxSumSubarray {
public int maxSubArray3(int[] nums) {
int maxSum = nums[0];
int sum = 0;
int minSum = 0;
for (int num : nums) {
// prefix Sum
sum += num;
// update maxSum
maxSum = Math.max(maxSum, sum - minSum);
// update minSum
minSum = Math.min(minSum, sum);
}
return maxSum;
}
}
Python 3:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
maxSum = nums[0]
minSum = sum = 0
for i in range(n):
sum += nums[i]
maxSum = max(maxSum, sum - minSum)
minSum = min(minSum, sum)
return maxSum
总结
我们使用四种方法解决了《最大子序列和问题》,
并详细分析了各个解法的思路以及复杂度,相信下次你碰到相同或者类似的问题
的时候也能够发散思维,做到一题多解,多题一解。
实际上,我们只是求出了最大的和,如果题目进一步要求出最大子序列和的子序列呢?
如果要题目允许不连续呢? 我们又该如何思考和变通?如何将数组改成二维,求解最大矩阵和怎么计算?
这些问题留给读者自己来思考。