1.Github项目地址:https://github.com/lydconsed/shudu
2.项目PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时 | 实际耗时 |
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | ||
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | ||
| · Design Spec | · 生成设计文档 | ||
| · Design Review | · 设计复审 (和同事审核设计文档) | ||
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | ||
| · Design | · 具体设计 | ||
| · Coding | · 具体编码 | ||
| · Code Review | · 代码复审 | ||
| · Test | · 测试(自我测试,修改代码,提交修改) | ||
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | ||
| · Size Measurement | · 计算工作量 | ||
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | ||
| 合计 |
|
3.解题思路描述
数独规则:满足每一行、每一列、每一个粗线宫内的数字均含1-9,不重复。
(1)生成数独终局
想法1,随机生成81个数,再按照数独规则检测来判断是否正确。(失败)
想法2,随机生成一行含有数字1~9的9个数,按一种方式变换生成其他8行。生成一串数字的种类有9!=362880种,但是少于1000000种。(失败)
想法3,用DFS生成数独,之后在末位不断改变生成不同数独,发现时间过长。生成效率过低。(失败)
想法4(尝试了很多,但是最后放弃),对于想法2进行改进, 产生多种变换方式以产生不同数独使其数量大于1000000种
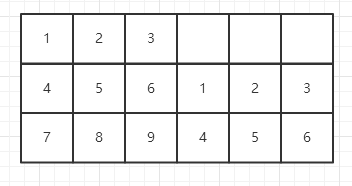
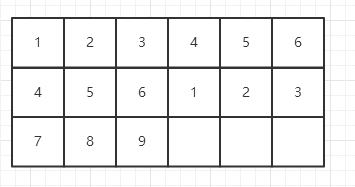
先生成1个9宫格,以1~9代表随机的9个不想等的数字
在同一行的第二个9宫格中,123的位置有两种,若123的位置在上方,则456可以有两种放置方法,123在下方,则456只能在最上,因此一共有3种放法。
之后这一行的3个9宫格中的数字可以确定
这一列的3个9宫格同理,其他方格则由约束条件得出。
因此一共可以产生8×9!
但是由于限制了第一个数字,实际产生的数独种类为8×8!=322560<1000000,因此失败
想法5,通过深搜来生成一个数独,然后通过对它的继续搜索来实现产生不同的数独,开始的时候,我以为完全通过深搜来生成数独花费的时间很长,后来经过测试,发现时间不到1s,之后的继续搜索也会比之前的速度快很多。
(2)解数独
关于解数独,原理与生成数独相似,都是通过深搜来生成数独。
之前也想通过剪枝的方法来减少时间,后来发现时间相差不大。
主要也是暴力深搜,之后也尝试了一下多线程,发现递归很难并行优化,之后也放弃了。
4.实现设计过程
之前想降低耦合,把几个不同模块分开。
但是发现会出现各种莫名bug,便放弃了。
主要分为3个模块,输入及处理,搜索算法,以及输出处理。
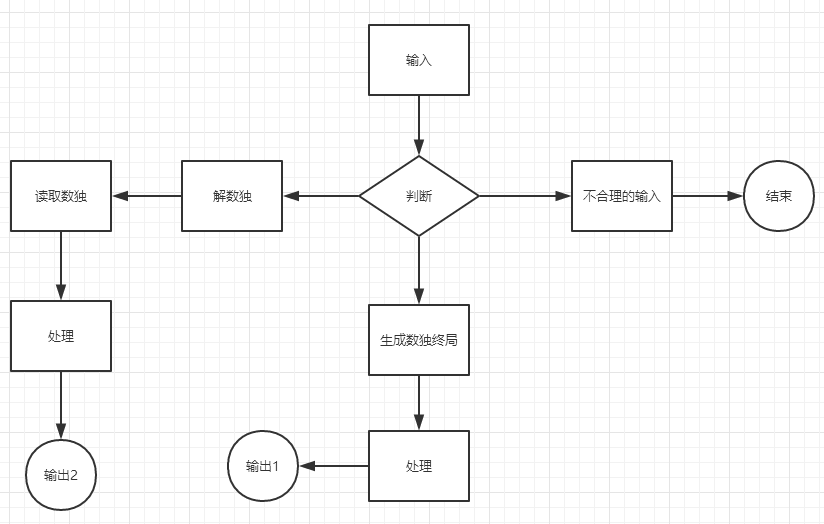
程序流程图
输入分为2种是因为对于输出结束的判断方法不一致,生成数独终局的输出结束是输出数量等于要求的数量,而解数独输出结束则是文件读取结束。
该代码一共有三条路径
单元测试用例
sudoku.exe -c 20 sudoku.exe -s C:\Users\0\OneDrive\1.txt sudoku.exe -p asfgasgasg
结果:
5.改进思路
开始时生成数独的算法
#include#include #include #include #include #include using namespace std; int sd[9][9]; int cp[9]; int num = 0; int ran() { return rand() % (9) + 1; } void sd_cp(int x1, int y1, int x2, int y2, bool ser) { if (ser == 1) { for (int i = 0; i < 3; i++) { sd[x2][y2] = sd[x1][y1]; x2++; x1++; } } if (ser == 0) { for (int i = 0; i < 3; i++) { sd[x2][y2] = sd[x1][y1]; y2++; y1++; } } } void pr() { for (int i = 0; i < 9; i++) { for (int j = 0; j < 9; j++) { printf("%d", sd[i][j]); if (j != 8) { printf(" "); } } printf("\n"); } printf("\n"); } void ran_cp() { cp[0] = 3; for (int i = 1; i < 9; i++) { while (1) { bool judge = 1; num = ran(); for (int j = 0; j < i; j++) { if (cp[j] == num) { judge = 0; break; } } if (judge == 1) { cp[i] = num; break; } } } num = 0; for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { sd[i][j] = cp[num]; num++; } } } void make_hang(int n,bool ser2) { if (ser2 == 0) { sd_cp(n * 3 + 0, 0, n * 3 + 1, 3, 0); sd_cp(n * 3 + 1, 0, n * 3 + 2, 3, 0); sd_cp(n * 3 + 2, 0, n * 3 + 0, 3, 0); sd_cp(n * 3 + 0, 0, n * 3 + 2, 6, 0); sd_cp(n * 3 + 1, 0, n * 3 + 0, 6, 0); sd_cp(n * 3 + 2, 0, n * 3 + 1, 6, 0); } else if (ser2 == 1) { sd_cp(n * 3 + 0, 0, n * 3 + 2, 3, 0); sd_cp(n * 3 + 1, 0, n * 3 + 0, 3, 0); sd_cp(n * 3 + 2, 0, n * 3 + 1, 3, 0); sd_cp(n * 3 + 0, 0, n * 3 + 1, 6, 0); sd_cp(n * 3 + 1, 0, n * 3 + 2, 6, 0); sd_cp(n * 3 + 2, 0, n * 3 + 0, 6, 0); } } void make_lie(bool ser1) { if (ser1 == 0) { sd_cp(0, 0, 3, 1, 1); sd_cp(0, 1, 3, 2, 1); sd_cp(0, 2, 3, 0, 1); sd_cp(0, 0, 6, 2, 1); sd_cp(0, 1, 6, 0, 1); sd_cp(0, 2, 6, 1, 1); } else if (ser1 == 1) { sd_cp(0, 0, 3, 2, 1); sd_cp(0, 1, 3, 0, 1); sd_cp(0, 2, 3, 1, 1); sd_cp(0, 0, 6, 1, 1); sd_cp(0, 1, 6, 2, 1); sd_cp(0, 2, 6, 0, 1); } } void final_sd(int n) { srand((unsigned)time(NULL)); for (int i = 0; i < n; i++) { ran_cp(); make_lie(ran()%2); for (int j = 0; j < 3; j++) { make_hang(j, ran()%2); } pr(); } }
生成的数独种类不够
后来改成了深搜,并且和解数独很相似。
主要是生成种类非常多,时间足够甚至可以输出所有数独。
改进后的性能分析图
可以看到深搜占用和最多的资源,判断占用了最多的时间。
由于没有进行多线程,cpu的总占用率不高。
判断主要是完全扫描(没有想出更好的优化办法)
深搜主要是搜索到第一个数独比较耗时,之后的搜索非常快。并不会导致程序表变慢。
消耗最大的是判断的函数,因为每次放置数字都要调用。
6.代码说明
两个主要函数
DFS()解数独
void DFS(int x, int y) { if (map[x][y] == 0) { if (x == 8 && y == 8) { fina = 1; return; } else if (y == 8) { DFS(x + 1, 0); if (fina == 1) { return; } if (map[x + 1][0] == 1) { sd[x + 1][0] = 0; } } else if (y != 8) { DFS(x, y + 1); if (fina == 1) { return; } if (map[x][y + 1] == 1) { sd[x][y + 1] = 0; } } } else if (map[x][y] == 1) { for (int i = 1; i <= 9; i++) { sd[x][y] = i; if (judge(x, y) == 0) { if (x == 8 && y == 8) { fina = 1; return; } else if (y == 8) { DFS(x + 1, 0); if (fina == 1)return; if (map[x + 1][0] == 1) { sd[x + 1][0] = 0; } } else if (y != 8) { DFS(x, y + 1); if (fina == 1)return; if (map[x][y + 1] == 1) { sd[x][y + 1] = 0; } } } } } }
sd为9×9数独,map为判断一个位置之前是否存在数字。1为不存在0为存在.
x,y为坐标,当x=8并且y=8时结束并输出。
每次回溯清空当前位置。
DFS2()生成数独
int DFS2(int x, int y) { for (int i = 1; i <= 9; i++) { sd[x][y] = i; if (judge(x, y) == 0) { if (x == 8 && y == 8) { pr(); pri_number++; if (pri_number == shudu_num) { printf("数独生成成功!\n"); exit(0); } fprintf(wri, "\n"); } if (y == 8) { DFS2(x + 1, 0); sd[x + 1][0] = 0; } else if (y != 8) { DFS2(x, y + 1); sd[x][y + 1] = 0; } } } }
与DFS相似,就是把它当作空数独的解暴力生成。
7.psp
8.总结
其中遇到了不少问题导致写代码出了很多问题,测试的时候发现结果都不对,又全推倒了重写,耗费了很多时间,同时也有许多人为的bug难以发现,导致测试总是出错。还是写的代码太少熟练度不太够。