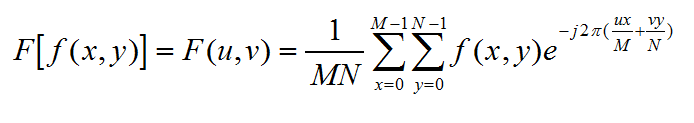python实现图像傅里叶变换

在做超分辨重建任务时，需要对重建图像做出评价，主要是人眼感官上的评价。这就需要我们从空域和频域两个方面对图像进行评价。下面给给出python实现的结果，并给出相应的代码。

图像(MxN)的二维离散傅立叶变换可以将图像由空间域变换到频域中去，空间域中用x,y来表示空间坐标，频域由u,v来表示频率，二维离散傅立叶变换的公式如下：

                      

在python中，numpy库的fft模块有实现好了的二维离散傅立叶变换函数，函数是fft2，输入一张灰度图，输出经过二维离散傅立叶变换后的结果，但是具体实现并不是直接用上述公式，而是用快速傅立叶变换。结果需要通过使用abs求绝对值才可以进行可视化，但是视觉效果并不理想，因为傅立叶频谱范围很大，所以要用log对数变换来改善视觉效果。

在使用log函数的时候，要写成log(1 + x) 而不是直接用log(x),这是为了避开对0做对数处理。

另外，图像变换的原点需要移动到频域矩形的中心，所以要对fft2的结果使用fftshift函数。最后也可以使用log来改善可视化效果。

代码如下：

import numpy as np
import matplotlib.pyplot as plt

img = plt.imread('FFT/baboon.png')
plt.subplot(231),plt.imshow(img),plt.title('picture')


#根据公式转成灰度图
img = 0.2126 * img[:,:,0] + 0.7152 * img[:,:,1] + 0.0722 * img[:,:,2]

#显示灰度图
plt.subplot(232),plt.imshow(img,'gray'),plt.title('original')


#进行傅立叶变换，并显示结果
fft2 = np.fft.fft2(img)
plt.subplot(233),plt.imshow(np.abs(fft2),'gray'),plt.title('fft2')


#将图像变换的原点移动到频域矩形的中心，并显示效果
shift2center = np.fft.fftshift(fft2)
plt.subplot(234),plt.imshow(np.abs(shift2center),'gray'),plt.title('shift2center')


#对傅立叶变换的结果进行对数变换，并显示效果
log_fft2 = np.log(1 + np.abs(fft2))
plt.subplot(235),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')


#对中心化后的结果进行对数变换，并显示结果
log_shift2center = np.log(1 + np.abs(shift2center))
plt.subplot(236),plt.imshow(log_shift2center,'gray'),plt.title('log_shift2center')
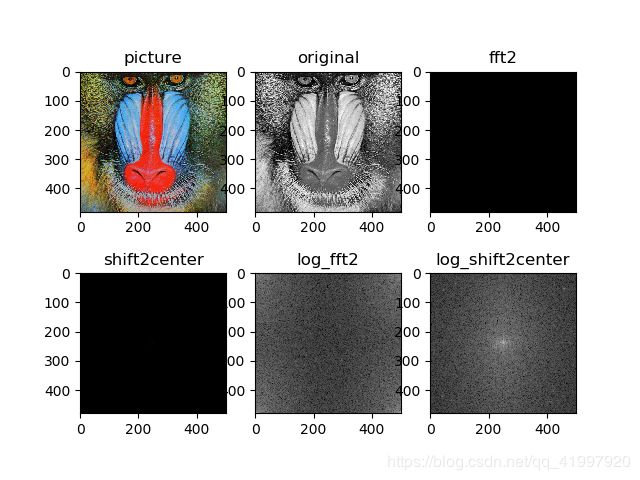
plt.show()

运行结果：

                   

###根据公式实现的二维离散傅立叶变换如下：
import numpy as np
import matplotlib.pyplot as plt
PI = 3.141591265
img = plt.imread('temp.jpg')

#根据公式转成灰度图
img = 0.2126 * img[:,:,0] + 0.7152 * img[:,:,1] + 0.0722 * img[:,:,2]

#显示原图
plt.subplot(131),plt.imshow(img,'gray'),plt.title('original')

#进行傅立叶变换，并显示结果
fft2 = np.fft.fft2(img)
log_fft2 = np.log(1 + np.abs(fft2))
plt.subplot(132),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')

h , w = img.shape
#生成一个同样大小的复数矩阵
F = np.zeros([h,w],'complex128')
for u in range(h):
    for v in range(w):
        res = 0
        for x in range(h):
            for y in range(w):
                res += img[x,y] * np.exp(-1.j * 2 * PI * (u * x / h + v * y / w))
        F[u,v] = res
log_F = np.log(1 + np.abs(F))
plt.subplot(133),plt.imshow(log_F,'gray'),plt.title('log_F')

直接根据公式实现复杂度很高，因为是四重循环，时间复杂度为O(M2N2)，所以实际用的时候需要用快速傅立叶变换来实现。

python实现快速傅里叶变换：

import cv

def FFT(image,flag = 0):
    w = image.width
    h = image.height
    iTmp = cv.CreateImage((w,h),cv.IPL_DEPTH_32F,1)
    cv.Convert(image,iTmp)
    iMat = cv.CreateMat(h,w,cv.CV_32FC2)
    mFFT = cv.CreateMat(h,w,cv.CV_32FC2)
    for i in range(h):
        for j in range(w):
            if flag == 0:
                num = -1 if (i+j)%2 == 1 else 1
            else:
                num = 1
            iMat[i,j] = (iTmp[i,j]*num,0)
    cv.DFT(iMat,mFFT,cv.CV_DXT_FORWARD)
    return mFFT
    
def IFFT(mat):
    mIFFt = cv.CreateMat(mat.rows,mat.cols,cv.CV_32FC2)
    cv.DFT(mat,mIFFt,cv.CV_DXT_INVERSE)
    return mIFFt

def Restore(mat):
    w = mat.cols
    h = mat.rows
    size = (w,h)
    iRestore = cv.CreateImage(size,cv.IPL_DEPTH_8U,1)
    for i in range(h):
        for j in range(w):
            num = -1 if (i+j)%2 == 1 else 1
            iRestore[i,j] = mat[i,j][0]*num/(w*h)
    return iRestore
        

def FImage(mat):
    w = mat.cols
    h = mat.rows
    size = (w,h)
    # iReal = cv.CreateImage(size,cv.IPL_DEPTH_8U,1)
    # iIma = cv.CreateImage(size,cv.IPL_DEPTH_8U,1)
    iAdd = cv.CreateImage(size,cv.IPL_DEPTH_8U,1)
    for i in range(h):
        for j in range(w):
            # iReal[i,j] = mat[i,j][0]/h
            # iIma[i,j] = mat[i,j][1]/h
            iAdd[i,j] = mat[i,j][1]/h + mat[i,j][0]/h
    return iAdd

    
def Filter(mat,flag = 0,num = 10):
    mFilter = cv.CreateMat(mat.rows,mat.cols,cv.CV_32FC2)
    for i in range(mat.rows):
        for j in range(mat.cols):
            if flag == 0:
                mFilter[i,j] = (0,0)
            else:
                mFilter[i,j] = mat[i,j]
    for i in range(mat.rows/2-num,mat.rows/2+num):
        for j in range(mat.cols/2-num,mat.cols/2+num):
            if flag == 0:
                mFilter[i,j] = mat[i,j]
            else:
                mFilter[i,j] = (0,0)
    return mFilter
    
image = cv.LoadImage('lena.jpg',0)    
mFFT = FFT(image)
mIFFt = IFFT(mFFT)
iAfter = FImage(mFFT)
mLP = Filter(mFFT)
mIFFt1=IFFT(mLP)
iLP = FImage(mLP)
iRestore = Restore(mIFFt1)

mHP = Filter(mFFT,1)
mIFFt2 = IFFT(mHP)
iHP = FImage(mHP)
iRestore2 = Restore(mIFFt2)

cv.ShowImage('image',image)
cv.ShowImage('iAfter',iAfter)
cv.ShowImage('iLP',iLP)
cv.ShowImage('iHP',iHP)
cv.ShowImage('iRestore',iRestore)
cv.ShowImage('iRestore2',iRestore2)

cv.WaitKey(0)

opencv实现傅里叶变换：

import numpy as np
import matplotlib.pyplot as plt
import cv2

img = cv2.imread('HR/baboon.png',0)
 
 
dft = cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)
 
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
 
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

参考文献：

【1】文献一

【2】文献二